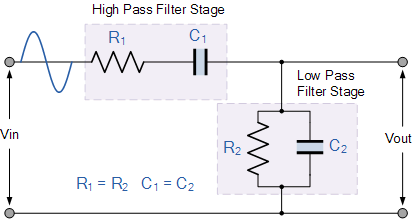
비엔나 브리지 발진기
Wien Bridge 발진기는 정현파 발진기를 생성하기 위해 함께 연결된 두 개의 RC 네트워크를 사용합니다.
RC 발진기 튜토리얼 에서 우리는 여러 개의 저항기와 커패시터를 반전 증폭기와 함께 연결하여 발진 회로를 생성할 수 있음을 확인했습니다. 정현파 출력 파형을 생성하기 위해 기존 LC 튜닝 탱크 회로 대신 RC 네트워크를 사용하는 가장 간단한 사인파 발진기 중 하나를 Wien 브리지 발진기 라고 합니다 .
빈 브리지 발진기 (Wien Bridge Oscillator) 는 회로가 휘트스톤 브리지 회로의 주파수 선택형 형태를 기반으로 하기 때문에 그렇게 불립니다. Wien Bridge 발진기는 공진 주파수 에서 안정성이 좋고 왜곡이 적으며 조정이 매우 쉬운 2단 RC 결합 증폭기 회로로 오디오 주파수 발진기로 널리 사용되는 회로이지만 출력 신호의 위상 변이가 상당히 큽니다. 이전 위상 변이 RC 발진기 와 다릅니다 .
빈 브리지 발진기는 주파수에 따라 위상 지연 또는 위상 전진 회로를 생성하는 동일한 구성 요소 값의 병렬 RC 와 연결된 직렬 RC 회로로 구성된 피드백 회로를 사용합니다 . 공진 주파수 fr 에서 위상 변이는 0o 입니다 . 아래 회로를 고려하십시오.
RC 위상 변이 네트워크
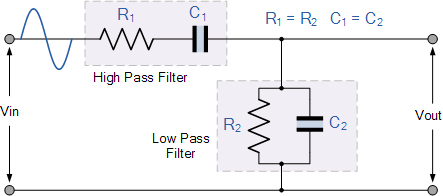
위의 RC 네트워크는 기본적으로 선택된 주파수 에서 높은 Q 인자 를 갖는 매우 선택적인 2차 주파수 의존형 대역 통과 필터를 생성하는 저역 통과 필터에 연결된 고역 통과 필터를 형성하는 병렬 RC 에 연결된 직렬 RC 회로 로 구성됩니다 . .
낮은 주파수에서는 직렬 커패시터( C1 )의 리액턴스가 매우 높으므로 개방 회로처럼 작동하여 Vin 의 모든 입력 신호를 차단하여 사실상 출력 신호 Vout이 발생하지 않습니다 . 마찬가지로, 고주파수에서는 병렬 커패시터( C2 )의 리액턴스가 매우 낮아지므로 이 병렬 연결된 커패시터는 출력 전체에서 약간 단락 회로처럼 작동하므로 다시 출력 신호가 없습니다.
따라서 C1 이 개방 회로이고 C2가 단락되는 두 극단 사이에 출력 전압 V OUT 이 최대값에 도달하는 주파수 지점이 있어야 합니다 . 이것이 발생하는 입력 파형의 주파수 값을 발진기 공진 주파수 ( ?r )라고 합니다.
이 공진 주파수에서 회로의 리액턴스는 저항과 같습니다. 즉, Xc = R 이고 입력과 출력 간의 위상차는 0도입니다. 따라서 출력 전압의 크기는 최대값이며 표시된 대로 입력 전압의 1/3(1/3)과 같습니다.
발진기 출력 이득 및 위상 변이
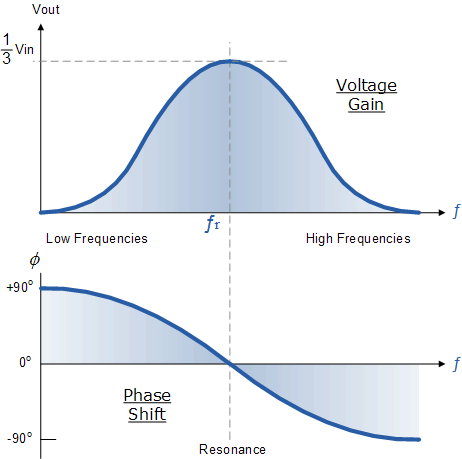
매우 낮은 주파수에서는 입력 신호와 출력 신호 사이의 위상 각도가 "양수"(위상 고급)인 반면, 매우 높은 주파수에서는 위상 각도가 "음수"(위상 지연)가 되는 것을 볼 수 있습니다. 이 두 지점의 중간에서 회로는 공진 주파수( fr )에 있고 두 신호는 "동위상" 또는 0o 입니다 . 따라서 우리는 다음 식으로 이 공진 주파수 지점을 정의할 수 있습니다.
비엔나 브리지 발진기 주파수
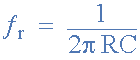
- 어디:
- fr은 헤르츠 단위의 공진 주파수입니다.
- R은 옴 단위의 저항입니다.
- C 는 패럿 단위의 커패시턴스입니다.
우리는 이전에 RC 네트워크의 출력 전압 Vout 의 크기가 최대값이고 입력 전압의 1/3(1/3)인 Vin 과 동일하여 발진이 발생할 수 있다고 말했습니다. 그런데 왜 3분의 1이 아닌 다른 가치가 있는 걸까요? 위 RC 회로의 출력이 1/3, 즉 0.333xVin 이 되어야 하는 이유를 이해하려면 연결된 두 RC 회로의 복소 임피던스( Z = R ± jX ) 를 고려해야 합니다 .
우리는 AC 이론 튜토리얼을 통해 복소 임피던스의 실수 부분이 저항 R 이고 허수 부분이 리액턴스 X 라는 것을 알고 있습니다 . 여기서는 커패시터를 다루므로 리액턴스 부분은 용량성 리액턴스 Xc 가 됩니다 .
RC 네트워크
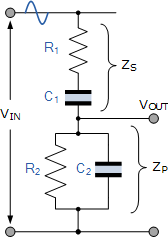
위의 RC 네트워크를 그림과 같이 다시 그리면 두 개의 RC 회로가 서로 연결되어 있고 접합부에서 가져온 출력으로 구성되어 있음을 명확하게 알 수 있습니다. 저항 R 1 과 커패시터 C 1은 상단 직렬 네트워크를 형성하고, 저항 R 2 와 커패시터 C 2는 하단 병렬 네트워크를 형성합니다.
그러므로 직렬 조합( R 1 C 1 )의 총 DC 임피던스를 Z S 라고 부를 수 있고 병렬 조합( R 2 C 2 ) 의 총 임피던스를 Z P 라고 부를 수 있습니다 . Z S 와 Z P 는 입력 V IN 에 걸쳐 효과적으로 직렬로 연결 되므로 그림과 같이 Z P 에서 가져온 출력으로 전압 분배기 네트워크를 형성합니다 .
그러면 R 1 및 R 2 의 구성 요소 값이 12kΩ 에서 동일하고 , 커패시터 C 1 및 C 2 가 3.9nF 에서 동일하며 , 공급 주파수 f 가 3.4kHz 라고 가정해 보겠습니다 .
직렬 회로
저항기 R 1 과 커패시터 C 1 의 직렬 조합의 총 임피던스는 다음과 같습니다.
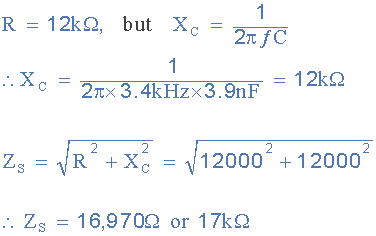
이제 우리는 3.4kHz의 공급 주파수에서 커패시터의 리액턴스가 12kΩ 의 저항기 저항과 동일하다는 것을 알고 있습니다 . 그러면 17kΩ 의 상위 직렬 임피던스 Z S 가 제공됩니다 .
더 낮은 병렬 임피던스 Z P 의 경우 두 구성 요소가 병렬이므로 병렬 회로의 임피던스가 이 병렬 조합의 영향을 받기 때문에 이를 다르게 처리해야 합니다.
병렬 회로
저항기 R 2 와 커패시터 C 2 가 포함 된 하위 병렬 조합의 총 임피던스는 다음과 같습니다.
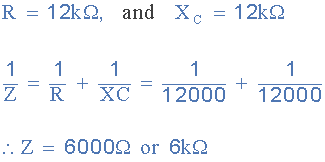
3400Hz 또는 3.4kHz의 공급 주파수에서 RC 병렬 회로의 결합된 DC 임피던스는 6kΩ ( R||Xc )이 되며 이 병렬 임피던스의 벡터 합은 다음과 같이 계산됩니다.
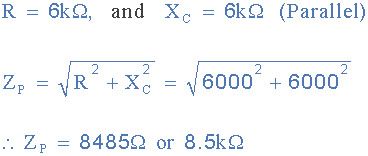
이제 직렬 임피던스의 벡터 합 값은 17kΩ (Z S = 17kΩ)이고 병렬 임피던스의 값은 8.5kΩ (Z P = 8.5kΩ)입니다. 따라서 주어진 주파수에서 전압 분배기 네트워크의 총 출력 임피던스 Zout은 다음과 같습니다.
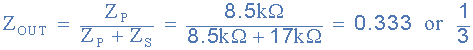
그러면 발진 주파수에서 출력 전압의 크기인 Vout은 Zout x Vin 과 같게 되며 이는 표시된 대로 입력 전압의 1/3(1/3)인 Vin 과 같 으며 이 주파수 선택형 RC 네트워크가 형성 됩니다. Wien Bridge 발진기 회로 의 기초 .
이제 1+R1/R2 의 이득을 갖는 비반전 증폭기에 이 RC 네트워크를 배치하면 다음과 같은 기본 Wien 브리지 발진기 회로가 생성됩니다.
빈 브리지 발진기
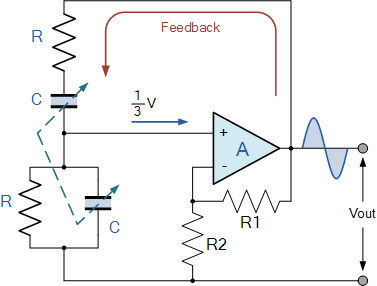
연산 증폭기의 출력은 증폭기의 두 입력 모두에 피드백됩니다. 피드백 신호의 한 부분은 R1 및 R2 의 저항 분배기 네트워크를 통해 반전 입력 단자(음성 또는 퇴행성 피드백)에 연결되어 증폭기 전압 이득을 좁은 한계 내에서 조정할 수 있습니다.
R과 C의 직렬 및 병렬 조합을 형성하는 다른 부분은 피드백 네트워크를 형성하고 RC Wien Bridge 네트워크 를 통해 비반전 입력 단자(양성 또는 재생성 피드백)로 피드백되며 이 양의 피드백 조합은 다음과 같습니다. 진동을 일으킵니다.
RC 네트워크는 증폭기의 포지티브 피드백 경로에 연결되며 단 하나의 주파수에 대해 위상 변이가 0입니다. 그런 다음 선택한 공진 주파수( fr )에서 반전 및 비반전 입력에 적용되는 전압은 동일하고 "동위상"이므로 포지티브 피드백이 네거티브 피드백 신호를 상쇄하여 회로가 진동하게 됩니다.
위에서 본 것처럼 입력이 출력의 1/3이기 때문에 발진이 시작되려면 증폭기 회로의 전압 이득이 3 "이득 = 3"보다 크거나 같아야 합니다. 이 값( Av ≥ 3 )은 피드백 저항 네트워크 R1 및 R2 에 의해 설정되며 비반전 증폭기의 경우 이는 비율 1+(R1/R2) 로 제공됩니다 .
또한 연산 증폭기의 개방 루프 이득 제한으로 인해 특수 고주파 연산 증폭기를 사용하지 않으면 1MHz 이상의 주파수를 달성할 수 없습니다.
Wien Bridge 발진기 예제 No1
10kΩ 의 저항과 1nF ~ 1000nF 의 가변 커패시터를 갖는 빈 브리지 발진기 회로 의 최대 및 최소 진동 주파수를 결정합니다 .
Wien Bridge Oscillator의 진동 주파수는 다음과 같이 지정됩니다.
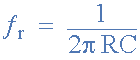
빈 브리지 발진기 최저 주파수
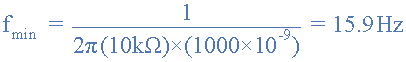
Wien Bridge 발진기 최고 주파수
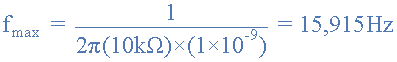
Wien Bridge 발진기 예제 No2
5,200Hz(5.2kHz)의 정현파를 생성하려면 빈 브리지 발진기 회로 가 필요합니다. 주파수 결정 저항 R1 및 R2 와 두 커패시터 C1 및 C2 의 값을 계산하여 필요한 주파수를 생성 합니다 .
또한 발진기 회로가 비반전 연산 증폭기 구성을 기반으로 하는 경우 필요한 발진을 생성하기 위해 이득 저항기의 최소값을 결정합니다. 마지막으로 결과 발진기 회로를 그립니다.
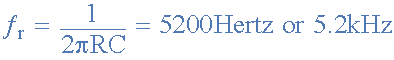
Wien Bridge Oscillator의 진동 주파수는 5200Hz로 지정되었습니다. 저항 R1 = R2 및 커패시터 C1 = C2 이고 피드백 커패시터 값을 3.0nF 로 가정하면 피드백 저항기의 해당 값은 다음과 같이 계산됩니다.
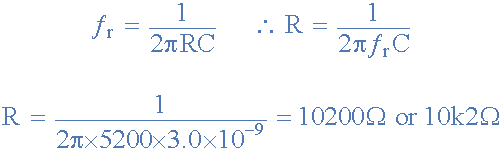
정현파 진동이 시작되려면 Wien Bridge 회로의 전압 이득이 3 ( Av ≥ 3 ) 보다 크거나 같아야 합니다 . 비반전 연산 증폭기 구성의 경우 이 값은 R3 및 R4 의 피드백 저항 네트워크에 의해 설정되며 다음과 같이 제공됩니다.
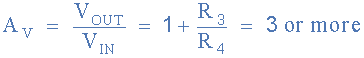
저항 R3 의 값을 100kΩ으로 선택하면 저항 R4 의 값은 다음과 같이 계산됩니다.
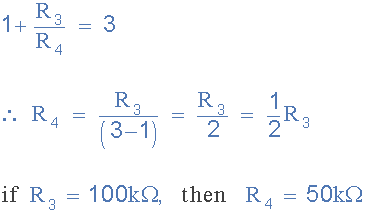
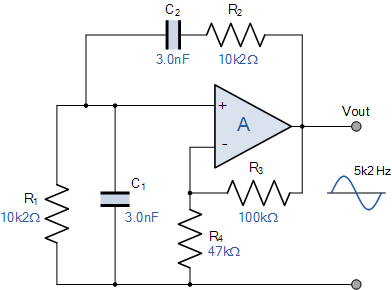
3 의 게인은 진동을 보장하는 데 필요한 최소 값이지만 실제로는 일반적으로 필요한 것보다 약간 더 높은 값이 필요합니다. 이득 값을 3.1 로 가정하면 저항 R4는 47kΩ 값을 제공하도록 다시 계산됩니다 . 이는 최종 Wien Bridge Oscillator 회로를 다음과 같이 제공합니다.
Wien Bridge 발진기 회로 예제 No2
Wien Bridge 발진기 요약
그런 다음 Wien Bridge 발진기 회로 에서 발진이 발생하려면 다음 조건을 적용해야 합니다.
- 입력 신호가 없으면 Wien Bridge Oscillator는 연속적인 출력 발진을 생성합니다.
- Wien Bridge 발진기는 넓은 범위의 주파수를 생성할 수 있습니다.
- 증폭기의 전압 이득은 3보다 커야 합니다.
- RC 네트워크는 비반전 증폭기와 함께 사용할 수 있습니다.
- RC 네트워크가 과부하되지 않고 필요한 조건을 변경하지 않도록 증폭기 의 입력 저항은 R 에 비해 높아야 합니다 .
- 외부 부하의 영향을 최소화하려면 증폭기의 출력 저항이 낮아야 합니다.
- 진동의 진폭을 안정화하는 몇 가지 방법이 제공되어야 합니다. 증폭기의 전압 이득이 너무 작으면 원하는 진동이 감소하여 중지됩니다. 너무 크면 출력이 공급 레일의 값으로 포화되어 왜곡됩니다.
- 피드백 다이오드 형태의 진폭 안정화를 통해 Wien Bridge 발진기의 발진이 무한정 계속될 수 있습니다.
발진기에 대한 마지막 검토에서는 수정 진동자를 탱크 회로로 사용하여 고주파수와 매우 안정적인 정현파 파형을 생성하는 수정 발진기를 살펴보겠습니다.