위상 변조: 이론, 시간 영역, 주파수 영역
우리는 모두 AM 라디오와 FM 라디오에 대해 들어보았을 것입니다. 하지만 위상 변조는 다른 범주에 속하는 것 같습니다. " PM 라디오"는 결코 흔한 용어가 아닙니다. 위상 변조는 디지털 RF의 맥락에서 더 관련성이 있는 것으로 밝혀졌습니다. 하지만 어떤 면에서는 위상 변조와 주파수 변조 사이에 차이가 거의 없기 때문에 PM 라디오가 FM 라디오만큼 흔하다고 말할 수 있습니다. FM과 PM은 각도 변조 의 두 가지 밀접하게 관련된 변형으로 간주하는 것이 가장 좋습니다 . 여기서 "각도"는 사인 또는 코사인 함수에 전달된 양의 수정을 나타냅니다.
수학
이전 페이지에서 주파수 변조는 기저대역 신호의 적분을 사인 또는 코사인 함수의 인수에 추가하여 달성된다는 것을 확인했습니다(여기서 사인 또는 코사인 함수는 캐리어를 나타냄):
xFM(t)=sin(\오메가Ct+∫−∞txBB(t)dt)
하지만 주파수 변조를 위상 변조에 대해 먼저 논의하면서 소개했다는 것을 기억하실 겁니다. 기저대역 신호 자체를 더하는 것이 아니라 기저대역 신호의 적분을 더하면 위상이 기저대역 값에 따라 달라집니다. 따라서 위상 변조는 실제로 주파수 변조보다 약간 더 간단합니다.
xPM(t)=sin(\오메가Ct+xBB(t))
주파수 변조와 마찬가지로 변조 지수를 사용하여 위상 변화를 기저대역 값의 변화에 더 민감하게 만들 수 있습니다.
xPM(t)=sin(\오메가Ct+mxBB(t))
위상 변조와 주파수 변조의 유사성은 단일 주파수 기저대역 신호를 고려하면 명확해집니다. x BB (t) = sin(ω BB t) 라고 합시다 . 사인의 적분은 음의 코사인(여기서는 무시할 수 있는 상수 포함)입니다. 즉, 적분은 단순히 원래 신호의 시간 이동 버전입니다. 따라서 이 기저대역 신호로 위상 변조와 주파수 변조를 수행하면 변조된 파형의 유일한 차이점은 기저대역 값과 캐리어의 변화 간의 정렬입니다. 변화 자체는 동일합니다. 이는 다음 섹션에서 더 명확해질 것이며, 여기서 시간 영역 플롯을 살펴볼 것입니다.
주파수 변조가 순간 주파수의 개념에 기반을 두는 것처럼 순간 위상을 다루고 있다는 점을 명심하는 것이 중요합니다. "위상"이라는 용어는 다소 모호합니다. 익숙한 의미 중 하나는 사인파의 초기 상태를 나타냅니다. 예를 들어 "일반" 사인파는 0의 값으로 시작한 다음 최대값으로 증가합니다. 주기의 다른 지점에서 시작하는 사인파에는 위상 오프셋이 있습니다. 위상을 전체 파형 주기의 특정 부분으로 생각할 수도 있습니다. 예를 들어 π/2의 위상에서 사인파는 주기의 1/4을 완료했습니다.
"위상"에 대한 이러한 해석은 기저대역 파형에 대한 응답으로 지속적으로 변하는 위상을 다룰 때 우리에게 큰 도움이 되지 않습니다. 오히려 우리는 순간 위상, 즉 주어진 순간의 위상이라는 개념을 사용하는데, 이는 삼각 함수에 전달된(주어진 순간에) 값에 해당합니다. 우리는 순간 위상의 이러한 연속적인 변화를 파형의 이전 상태에서 캐리어 값을 더 멀리 또는 더 가깝게 "밀어내는" 것으로 생각할 수 있습니다.
기억해야 할 또 다른 사항: 사인과 코사인을 포함한 삼각 함수는 각도에서 작동합니다. 삼각 함수의 인수를 변경하는 것은 각도를 변경하는 것과 동일하며, 이것이 FM과 PM이 모두 각도 변조로 설명되는 이유를 설명합니다.
시간 도메인
FM 논의에 사용한 것과 동일한 파형, 즉 10MHz 캐리어와 1MHz 사인파 기저대역 신호를 사용하겠습니다.
이전 페이지에서 본 FM 파형(m = 4)은 다음과 같습니다.
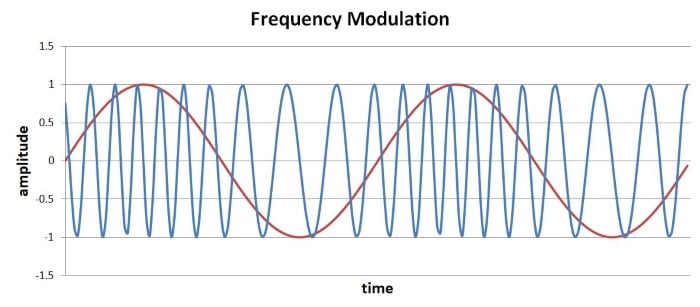
다음 방정식을 사용하여 PM 파형을 계산할 수 있습니다. 여기서 캐리어 파동의 인수에 추가된 신호는 음의 코사인(즉, 원래 신호의 적분) 대신 양의 사인(즉, 원래 신호)을 사용합니다.
xPM(t)=sin((10×106×2πt)+sin(1×106×2πt))
총리의 음모는 다음과 같습니다.

이에 대해 논의하기 전에 FM 파형과 PM 파형을 보여주는 플롯도 살펴보겠습니다.

여기서 가장 먼저 떠오르는 것은 시각적 관점에서 FM이 PM보다 더 직관적이라는 것입니다. 변조된 파형의 고주파 및 저주파 구간과 고주파 및 저주파 베이스밴드 값 사이에 명확한 시각적 연결이 있습니다. PM의 경우 베이스밴드 파형과 캐리어 동작 간의 관계가 즉시 명확하지 않을 수 있습니다. 그러나 약간 살펴보면 PM 캐리어 주파수가 베이스밴드 파형의 기울기 에 해당한다는 것을 알 수 있습니다 . 가장 높은 주파수 구간은 x BB 의 가장 가파른 양의 기울기 동안 발생 하고 가장 낮은 주파수 구간은 가장 가파른 음의 기울기 동안 발생합니다.
이는 말이 됩니다. 주파수(시간의 함수)는 위상(시간의 함수)의 미분이라는 점을 기억하세요. 위상 변조의 경우 기저대역 신호의 기울기는 위상이 얼마나 빨리 변하는지를 결정하고 위상이 변하는 속도는 주파수와 동일합니다. 따라서 PM 파형에서 높은 기저대역 기울기는 높은 주파수에 해당하고 낮은 기저대역 기울기는 낮은 주파수에 해당합니다. 주파수 변조의 경우 x BB 의 적분을 사용하는데, 이는 기저대역 파형의 높은(또는 낮은) 기울기 부분 다음에 높은(또는 낮은) 주파수 캐리어 섹션을 기저대역 값으로 이동하는 효과가 있습니다 .
주파수 영역
앞의 시간 영역 플롯은 이전에 말한 내용을 보여줍니다. 주파수 변조와 위상 변조는 매우 유사합니다. 따라서 주파수 영역에서 PM의 효과가 FM의 효과와 유사하다는 것은 놀라운 일이 아닙니다. 위에서 사용한 캐리어 및 기저대역 신호에 대한 위상 변조 스펙트럼은 다음과 같습니다.


요약
- 위상 변조는 반송파를 나타내는 사인 또는 코사인 함수의 인수에 기저대역 신호를 더하여 계산됩니다.
- 변조 지수는 위상 변화를 기저대역 신호의 동작에 따라 더 민감하게 또는 덜 민감하게 만듭니다.
- 위상 변조의 주파수 영역 효과는 주파수 변조의 효과와 유사합니다.
- 아날로그 위상 변조는 일반적이지 않습니다. 그러나 디지털 위상 변조는 널리 사용됩니다.우리는 모두 AM 라디오와 FM 라디오에 대해 들어보았을 것입니다. 하지만 위상 변조는 다른 범주에 속하는 것 같습니다. " PM 라디오"는 결코 흔한 용어가 아닙니다. 위상 변조는 디지털 RF의 맥락에서 더 관련성이 있는 것으로 밝혀졌습니다. 하지만 어떤 면에서는 위상 변조와 주파수 변조 사이에 차이가 거의 없기 때문에 PM 라디오가 FM 라디오만큼 흔하다고 말할 수 있습니다. FM과 PM은 각도 변조 의 두 가지 밀접하게 관련된 변형으로 간주하는 것이 가장 좋습니다 . 여기서 "각도"는 사인 또는 코사인 함수에 전달된 양의 수정을 나타냅니다.수학
주파수 변조가 순간 주파수의 개념에 기반을 두는 것처럼 순간 위상을 다루고 있다는 점을 명심하는 것이 중요합니다. "위상"이라는 용어는 다소 모호합니다. 익숙한 의미 중 하나는 사인파의 초기 상태를 나타냅니다. 예를 들어 "일반" 사인파는 0의 값으로 시작한 다음 최대값으로 증가합니다. 주기의 다른 지점에서 시작하는 사인파에는 위상 오프셋이 있습니다. 위상을 전체 파형 주기의 특정 부분으로 생각할 수도 있습니다. 예를 들어 π/2의 위상에서 사인파는 주기의 1/4을 완료했습니다.기억해야 할 또 다른 사항: 사인과 코사인을 포함한 삼각 함수는 각도에서 작동합니다. 삼각 함수의 인수를 변경하는 것은 각도를 변경하는 것과 동일하며, 이것이 FM과 PM이 모두 각도 변조로 설명되는 이유를 설명합니다.FM 논의에 사용한 것과 동일한 파형, 즉 10MHz 캐리어와 1MHz 사인파 기저대역 신호를 사용하겠습니다.이전 페이지에서 본 FM 파형(m = 4)은 다음과 같습니다.

이는 말이 됩니다. 주파수(시간의 함수)는 위상(시간의 함수)의 미분이라는 점을 기억하세요. 위상 변조의 경우 기저대역 신호의 기울기는 위상이 얼마나 빨리 변하는지를 결정하고 위상이 변하는 속도는 주파수와 동일합니다. 따라서 PM 파형에서 높은 기저대역 기울기는 높은 주파수에 해당하고 낮은 기저대역 기울기는 낮은 주파수에 해당합니다. 주파수 변조의 경우 x BB 의 적분을 사용하는데, 이는 기저대역 파형의 높은(또는 낮은) 기울기 부분 다음에 높은(또는 낮은) 주파수 캐리어 섹션을 기저대역 값으로 이동하는 효과가 있습니다 .앞의 시간 영역 플롯은 이전에 말한 내용을 보여줍니다. 주파수 변조와 위상 변조는 매우 유사합니다. 따라서 주파수 영역에서 PM의 효과가 FM의 효과와 유사하다는 것은 놀라운 일이 아닙니다. 위에서 사용한 캐리어 및 기저대역 신호에 대한 위상 변조 스펙트럼은 다음과 같습니다. 요약
요약
- 위상 변조는 반송파를 나타내는 사인 또는 코사인 함수의 인수에 기저대역 신호를 더하여 계산됩니다.
- 변조 지수는 위상 변화를 기저대역 신호의 동작에 따라 더 민감하게 또는 덜 민감하게 만듭니다.
- 위상 변조의 주파수 영역 효과는 주파수 변조의 효과와 유사합니다.
- 아날로그 위상 변조는 일반적이지 않습니다. 그러나 디지털 위상 변조는 널리 사용됩니다.

- 주파수 영역
- 여기서 가장 먼저 떠오르는 것은 시각적 관점에서 FM이 PM보다 더 직관적이라는 것입니다. 변조된 파형의 고주파 및 저주파 구간과 고주파 및 저주파 베이스밴드 값 사이에 명확한 시각적 연결이 있습니다. PM의 경우 베이스밴드 파형과 캐리어 동작 간의 관계가 즉시 명확하지 않을 수 있습니다. 그러나 약간 살펴보면 PM 캐리어 주파수가 베이스밴드 파형의 기울기 에 해당한다는 것을 알 수 있습니다 . 가장 높은 주파수 구간은 x BB 의 가장 가파른 양의 기울기 동안 발생 하고 가장 낮은 주파수 구간은 가장 가파른 음의 기울기 동안 발생합니다.

- 이에 대해 논의하기 전에 FM 파형과 PM 파형을 보여주는 플롯도 살펴보겠습니다.

- 총리의 음모는 다음과 같습니다.
- xPM(t)=sin((10×106×2πt)+sin(1×106×2πt))
- 다음 방정식을 사용하여 PM 파형을 계산할 수 있습니다. 여기서 캐리어 파동의 인수에 추가된 신호는 음의 코사인(즉, 원래 신호의 적분) 대신 양의 사인(즉, 원래 신호)을 사용합니다.
- 시간 도메인
- "위상"에 대한 이러한 해석은 기저대역 파형에 대한 응답으로 지속적으로 변하는 위상을 다룰 때 우리에게 큰 도움이 되지 않습니다. 오히려 우리는 순간 위상, 즉 주어진 순간의 위상이라는 개념을 사용하는데, 이는 삼각 함수에 전달된(주어진 순간에) 값에 해당합니다. 우리는 순간 위상의 이러한 연속적인 변화를 파형의 이전 상태에서 캐리어 값을 더 멀리 또는 더 가깝게 "밀어내는" 것으로 생각할 수 있습니다.
- 위상 변조와 주파수 변조의 유사성은 단일 주파수 기저대역 신호를 고려하면 명확해집니다. x BB (t) = sin(ω BB t) 라고 합시다 . 사인의 적분은 음의 코사인(여기서는 무시할 수 있는 상수 포함)입니다. 즉, 적분은 단순히 원래 신호의 시간 이동 버전입니다. 따라서 이 기저대역 신호로 위상 변조와 주파수 변조를 수행하면 변조된 파형의 유일한 차이점은 기저대역 값과 캐리어의 변화 간의 정렬입니다. 변화 자체는 동일합니다. 이는 다음 섹션에서 더 명확해질 것이며, 여기서 시간 영역 플롯을 살펴볼 것입니다.
- xPM(t)=sin(\오메가Ct+mxBB(t))
- 주파수 변조와 마찬가지로 변조 지수를 사용하여 위상 변화를 기저대역 값의 변화에 더 민감하게 만들 수 있습니다.
- xPM(t)=sin(\오메가Ct+xBB(t))
- 하지만 주파수 변조를 위상 변조에 대해 먼저 논의하면서 소개했다는 것을 기억하실 겁니다. 기저대역 신호 자체를 더하는 것이 아니라 기저대역 신호의 적분을 더하면 위상이 기저대역 값에 따라 달라집니다. 따라서 위상 변조는 실제로 주파수 변조보다 약간 더 간단합니다.
- xFM(t)=sin(\오메가Ct+∫−∞txBB(t)dt)
- 이전 페이지에서 주파수 변조는 기저대역 신호의 적분을 사인 또는 코사인 함수의 인수에 추가하여 달성된다는 것을 확인했습니다(여기서 사인 또는 코사인 함수는 캐리어를 나타냄):

