베이스 전류의 효과를 무시하고, PNP 트랜지스터는 전압-전류 특성이 양의 세로축에서 적절히 이동된 단일 pn 접합과 동일하다는 것을 보여줄 것입니다. 이를 통해 이 장치의 전압 증폭을 빠르게 결정할 수 있습니다.
추상적 도식화 – 단일 접합으로서의 트랜지스터
이전 호의 결과를 염두에 두고, 부하 저항 R L 을 가진 활성 영역에 PNP 트랜지스터가 있는 그림 1의 계획을 살펴보겠습니다. 참신한 점은 수학적 단계를 더 명확하게 하기 위해 보조 변수 x, y, z, ξ를 도입했다는 것입니다 . 따라서 y는 에미터-베이스 접합 J E 를 통해 흐르는 에미터 전류입니다 . 기호의 명확한 의미와 함께 다음과 같습니다.

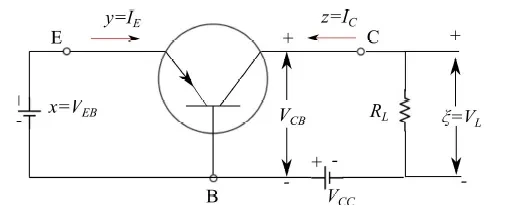
이전 호에서 본 것처럼:

그림 1의 다이어그램에서 I C 의 방향은 일반적인 방향임을 주목하세요 . 전하 캐리어(홀)가 반대 방향으로 이동하므로 방정식(2)에서 I C < 0입니다.
방정식(2)에서 0 < α < 1이고, 여기서 α는 대략 1(베이스의 전자와 재결합하지 않는 에미터에 의해 확산된 홀의 비율)과 같습니다. 적절한 도핑을 사용하면 α = 1을 얻을 수 있습니다.
실수 변수 f : X → Y 의 모든 실수 함수는 수량 x를 입력으로 받고 수량 y를 출력으로 반환하는 장치로 해석될 수 있습니다 . 이 프로세스는 그림 2의 지향 다이어그램으로 표현됩니다.

우리의 경우, y는 에미터 전류이므로 콜렉터-베이스 접합 J C를 구현하는 장치의 입력을 구성하고 , 그 출력은 z = g ( y )이고 g ( y ) = − αy + I C 0 입니다. 후자는 저항 부하 R L 로 구성된 장치의 입력이므로 ξ = R L | z | = − R L z 입니다 . 방향성 다이어그램의 관점에서, 우리는 그림 3의 블록 다이어그램을 가지고 있습니다.

수학적 해석학에서 잘 알려져 있듯이 이는 합성 함수 ξ = h ( g ( f ( x )))를 고려하는 것과 동일합니다. 즉 다음과 같습니다.
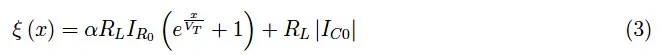
따라서 ξ ( x ) /R L은 | I C 0 | 의 세로축의 양의 방향으로 변환된 접합 다이오드의 전압-전류 특성입니다 . 따라서 우리는 다음과 같은 결론에 도달했습니다.
베이스 전류를 무시하면, PNP 트랜지스터는 전압-전류 특성이 | I C 0 | 만큼 이동한 단일 pn 접합과 동등합니다 .
전압 증폭
그림 4에서는 정상 조건을 고려하고 있는 저항 부하 RL 의 양단 전압을 V EB 의 함수로 표현하는 함수(3)의 그래프를 보고합니다 .

여기서 V γ 는 J E 의 오프셋 전압입니다 . 이 바이어스 전압 값은 J E 의 작동점 ( x 0 , y 0 ) 을 고유하게 결정하고 따라서 데카르트 평면 xξ 에서 P 0 ( x 0 , ξ 0 )을 결정합니다 .
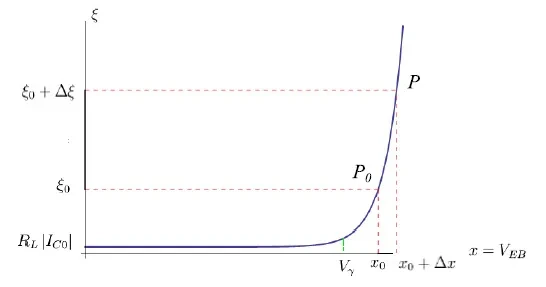
진폭이 ∆ x ≪ 1인 신호(즉, 약한 신호) 를 x 0 에 중첩하면 그림 4와 같이 동작점이 Q
로 이동합니다. 물리적 변수를 일시적으로 복원하면 기호의 명확한 의미인 ∆ x = V in , ∆ ξ = V out 을 얻을 수 있습니다 . 그래프에서 V out ≫ V in 이므로 전압 증폭이 발생하고 이를 정량화하려고 합니다. 이는 순방향 바이어스 조건에서 접합은 거의 단락 회로이기 때문입니다.
유명한 해석학 정리( 미분 정리 )에 대해서는 다음과 같습니다.

여기서 o (∆ x )는 증분 ∆ x 보다 더 높은 차수 항을 나타내고 , dξ = ξ ′ ( x )∆ x 는 함수 ξ ( x ) 의 미분입니다 . 우리는 x 0 의 1차 도함수에서 가정한 값에 관심이 있습니다 . 계산이 완료되면 다음과 같습니다.

여기서 r (0)은 x 0 에서 계산된 J E 의 차동 저항입니다 . ∆ x 의 작은 증가를 고려하고 있으므로 방정식(5)에서 고차 항을 무시할 수 있습니다.

이는 다음과 같습니다.

여기서 무차원 양 A 는 전압 증폭입니다. α 는 대략 1이므로 A는 부하 저항과 J E 의 차동 저항의 비율에 따라 달라집니다 . 후자의 일반적인 값은 40Ω입니다. 따라서 3000Ω의 부하에 대해 A = +75입니다.
에너지 고려 사항
에너지적으로는 다음과 같이 진행할 수 있습니다. 입력 신호 V in = ∆ x 와 관련된 전력을 P in 으로 표시하므로 P in = ∆ x ∆ y 입니다 . 이 마지막 항은 컬렉터 전류의 증가입니다. 마찬가지로 P out 은 출력 신호 P out = R L (∆ z ) 2 와 관련된 전력입니다 . 계산이 완료되면:

우리는 부등식 P out ≫ P in 이 에너지 보존 원리를 위반하지 않는다는 것을 관찰함으로써 결론을 내립니다. 왜냐하면 직접 계산하면 다음과 같은 결과가 나오기 때문입니다.

오른쪽의 두 번째 항은 이미터와 컬렉터 접합을 모두 바이어스하는 전압 생성기에서 전달되는 전력입니다.