이 튜토리얼에서는 트랜지스터의 이미터가 입력/출력 인터페이스 역할을 하는 일반적인 이미터 구성(가장 많이 사용됨)을 공부합니다.
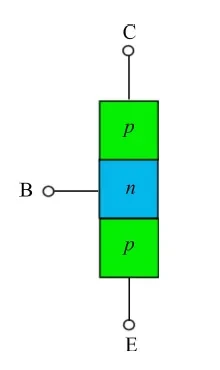
공통 에미터 구성에서 입력/출력 루프는 에미터를 공유합니다. 먼저 공통 베이스 구성 에서 공통 에미터 구성으로 이동하는 방법을 살펴보겠습니다. 평소처럼 PNP 트랜지스터를 참조하고 일반성을 잃지 않고 장치가 활성 영역으로 설정되어 있다고 가정해 보겠습니다. 순방향 바이어스 에미터 접합, 역방향 바이어스 컬렉터 접합(그림 1).
이제 다음과 같은 작업을 수행합니다.
- 편파를 분리합니다.
- 그림 2와 같이 도면 평면에서 +π/2(즉, 반시계 방향) 회전을 수행합니다.
- 이전 구성과 비교하여 거울상 구성을 만들기 위해 공간 반사를 수행합니다(그림 3).
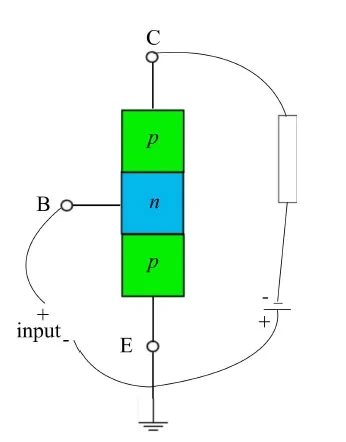
- 재분극: 방출기를 접지에 연결한 후 부하를 연결하고 전원을 켭니다(그림 4).
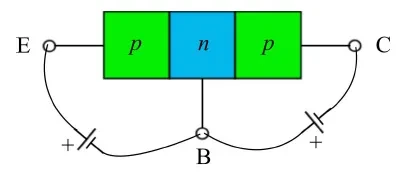
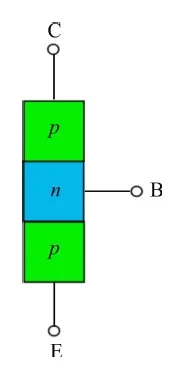
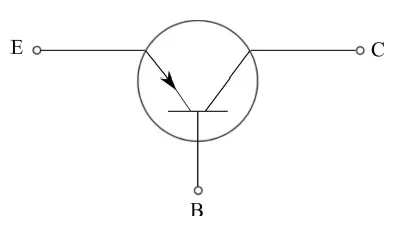
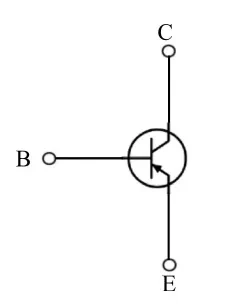
방금 본 것은 물리적 레이아웃입니다. 회로도를 살펴보겠습니다. 그림 5에서 공통 베이스 PNP 트랜지스터의 기호를 떠올려보고, 그림 6에서는 공통 에미터 PNP 트랜지스터를 보여줍니다.
이제 그림 7에 표시된 회로도를 살펴보겠습니다. 관례에 따라 V CC > 0(공급 전압)이 가정됩니다. 입력 전류는 I B 이고 V CE 는 출력 전압입니다. 따라서 관련된 양은 다음과 같습니다.

전류 I E 는 에미터가 입력과 출력 사이의 인터페이스 역할을 하기 때문에 결정적인 역할을 하지 않습니다. 따라서 가능한 독립 변수 선택을 위해 이 양을 제외합니다. 베이스 전류 I B 는 입력 전압 V BE 와 기능적으로 연결되어 있으며 , 이러한 상황은 이 쌍을 독립 변수로 제외합니다. 그러나 이것들은 트랜지스터의 전기적 동작을 연구하는 데 중요한 양이므로 둘 중 하나를 독립 변수로 가정합니다. 이러한 목적을 위해 전류 I B 를 취하는 것이 일반적입니다. 출력 메시에서 I C 와 V CE 를 찾습니다 . 출력 전압 V CE 를 독립 변수로 가정합니다 . 요약하면 (V CE , I B )가 우리가 찾고 있던 독립 변수 쌍입니다. 나머지 양의 함수적 종속성은 다음과 같습니다.
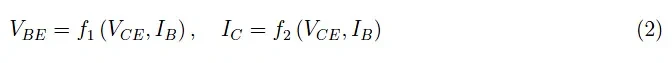
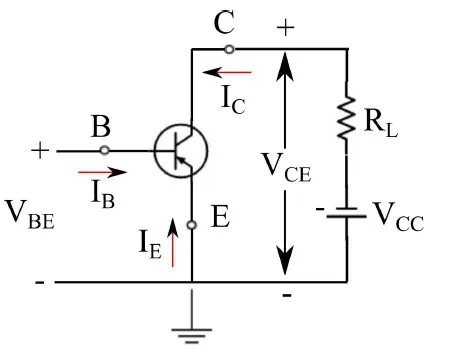
특성을 그래프로 표현하려면 모든 장치에 대해 전압 대 전류 또는 그 반대로 표현해야 한다는 점을 기억하세요.
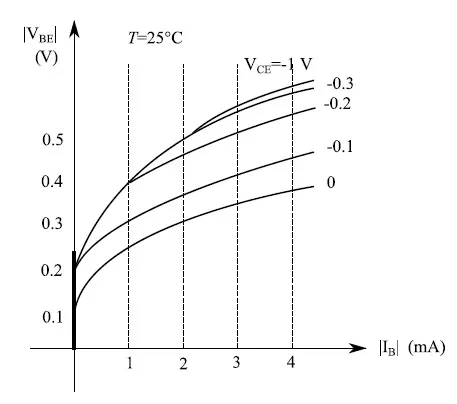
방정식(2)의 첫 번째 부분에서 V CE를 주어진 값 범위에서 가변 매개변수로 가정하는 것이 자연스럽고, 베이스 전류 I B 는 독립 변수입니다. 따라서 우리는 주어진 출력 전압 값에 대해 베이스 전류의 함수로서 입력 전압이 어떻게 변하는지 알려주는 입력 특성(더 정확히는 특성 계열)을 가지고 있습니다.
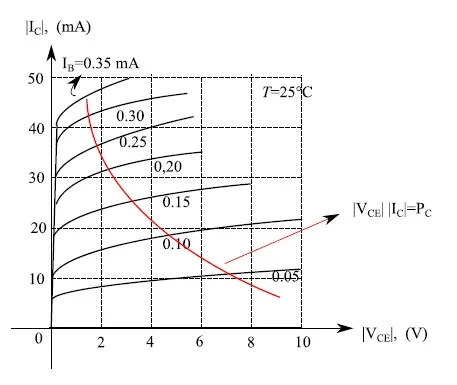
마찬가지로 방정식(2)의 두 번째 부분에서 베이스 전류 I B 는 주어진 값 범위에서 가변 매개변수로 가정되고 출력 전압 V CE 는 독립 변수입니다. 따라서 우리는 베이스 전류의 주어진 값에 대해 출력 전압의 함수로서 컬렉터 전류가 어떻게 변하는지 알려주는 출력 특성(더 정확히는 특성 계열)을 갖게 됩니다.
이제 개별 수량의 부호를 설정해 보겠습니다. 그림 7에 표시된 극성을 가진 V CC > 0은 이 전류를 배향한 방식 때문에 I C < 0을 의미합니다. 다른 전류와 전압의 음수 부호가 뒤따릅니다. 이것을 지정했으면 그림 8에 입력 특성을 플로팅하고 그림 9에 출력 특성을 그래프로 표시합니다. 두 경우 모두 전형적인 지수적 상승 추세를 알 수 있습니다. 그림 9에서 빨간색 곡선은 한계 소산 곡선 , 즉 출력 메시에서 일정한 소산 전력 지점의 기하학적 궤적입니다. 이 곡선 위의 작업 지점은 더 큰 소산 전력에 해당합니다.