전력 전자공학에 대한 이 노트 컬렉션은 다음과 같이 구성되어 있습니다.
- 문제에 대한 수학적 접근 방식
- Mathematica 컴퓨팅 환경에서 솔루션 구현 1-2
- 얻은 결과의 물리적 해석. Mathematica 코드는 여기에 포함되지 않습니다. 동등한 소프트웨어 도구를 사용할 수 있기 때문입니다.
이 튜토리얼을 읽기 위한 요구 사항은 전기 공학에 대한 기본 지식입니다. 3
분해 SiC/GaN 대 Si/Ge
다음 두 가지로 나뉜 문제를 풀어야 한다고 가정해 보겠습니다.
- 그림 1과 그림 2에 표시된 그래프를 정당화하여 WBG 다이오드 의 파괴 현상을 해석하십시오 .
- 제너 다이오드의 안정화 특성을 손상시키지 않으면서 그림 3의 δV를 추정할 수 있는 기준은 무엇입니까?


v > 0 의 경우 다이오드는 순방향 전압 모드에 있고, v < 0의 경우 역방향 전압 또는 차단 모드 에 있습니다 . 역방향 전압 모드에서는 다음과 같습니다.

이 상태에서 다이오드의 동적 전도도 4는 거의 0입니다(무한 동적 저항). 역방향 바이어스 전압을 점진적으로 증가시키면 전하 캐리어 생성 프로세스가 특이점으로 "폭발"합니다(적어도 이론적으로는):

여기서 임계값 v B < 0은 파괴 전압 , 즉 역포화 전류가 극적으로 증가하는 전압입니다. 이 특이한 동작은 두 가지 메커니즘으로 설명됩니다.
- 눈사태 증식
- 제너 효과.
눈사태 증식은 전기장의 세기가 증가하여 공유 결합이 끊어지는 데서 기인합니다. 격자 이온의 충돌로 방출된 해당 전자/홀 쌍은 새로운 쌍을 생성하고, 이런 식으로 계속됩니다.
반면, 제너 효과는 격자 이온을 포함하지 않습니다. 회로 응용 분야에서 두 효과는 구별되지 않습니다. 따라서 우리는 단순히 제너 효과를 참조하고 제너 전압을 V z = − v B 로 설정하여 정의합니다 .
또한 밴드갭의 진폭 ε g가 온도가 증가함에 따라 감소하는 반면 역포화 전류는 증가한다는 점을 기억합니다. 그러면 제너 전압이 밴드갭에 비례한다는 것을 쉽게 이해할 수 있습니다. 더 정확히 말하면 Si/Ge 다이오드의 경우 1볼트 미만에서 SiC/GaN 다이오드의 경우 5000볼트까지입니다. 또한 i 0가 상당히 증가합니다. Si/Ge의 경우 일반적인 값은 1~ 10µA 범위입니다 .
질문 2에 대한 솔루션
알다시피, 제너 다이오드는 전압 안정기로 사용됩니다. 고전력 프로세스를 포함하지 않는 회로에서는 약 10볼트의 안정화가 필요합니다. 우리는 0 < δV < − v B 인 v > v B + δV 에 대한 전압-전류 특성을 사용하여 그림 3의 곡선을 그린 다음, 접합점에서 1차 도함수의 연속성을 부과할 수 없는 "테스트 함수"의 그래프와 연결했습니다. 사실, 다이오드의 동적 저항의 불연속성에 해당하는 전형적인 "날카로운 무릎"을 주목합니다. 원칙적으로 작은 증분 δV 는 다이오드 제조업체가 제공한 임계값 아래의 전류 값에서 떨어지지 않도록 고정됩니다(그렇지 않으면 안정화가 없습니다).
전압 안정기
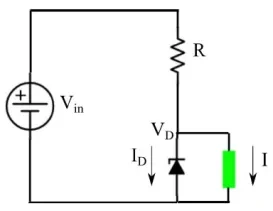
그림 4에 표시된 회로도에는 다음 특성을 가진 장치가 포함됩니다. V L =5V 및 I L =50mA. 또한 전압 V in =15V를 제공하는 전원 공급 장치가 있습니다. 작동 지점 V z =5.1V 및 I z =50mA, 최대 전력 소모가 0.5W인 제너 다이오드를 사용하여 부하의 전류가 변할 수 있는 범위를 확인합니다.
해결책
이상적인 제너 다이오드의 경우 전압-전류 특성은 그림 5에 표시된 추세를 갖습니다. 그러나 그림 6에 표시된 대로 해당 양을 대문자로 표시하여 절대 값으로 전환하는 것이 좋습니다.

이론적으로 V D = V z (이 값은 다이오드 제조업체에서 제공) 이면 전류는 0에서 +∞까지 변할 수 있습니다. 현실적으로 전류의 최대값은 다이오드가 소산할 수 있는 최대 전력 W max
를 발생시키는 값입니다(이 수치적 데이터도 제조업체 에서 제공 ). 따라서 다음이 성립합니다.

이러한 동작은 그림 6에 나타나 있으며, 여기서 A ( Vz , Iz ) 는 작업 지점( Iz = 알려진 수치 데이터)입니다.

키르히호프의 제2법칙을 적용하면 다음과 같습니다.

오른쪽에는 부하의 전류 I가 있는데, 그 크기는 정격 값 I L 주위에서 변동할 수 있습니다 . 다이오드는 I = I L 인 경우 I D = I z 가 되도록 구성됩니다 . V D = V z 로 설정하면 방정식(5)은 다음과 같이 됩니다.

이를 통해 회로에 삽입할 저항 R 의 값을 계산할 수 있습니다.

따라서 우리는 다음과 같이 쓸 수 있습니다.

이를 통해 부하 전류를 다이오드 전류의 함수로 표현할 수 있습니다.

해당 플롯은 그림 7에 나와 있습니다. 이제 다음과 같이 안정성 범위를 얻을 수 있습니다.

즉, 부하 전류가 방정식(10)에서 주어진 범위 내에서 변하면 전압은 V L 에서 안정을 유지합니다 . 이제 우리가 해야 할 일은 숫자 값을 방정식에 대입하는 것뿐입니다. 다음을 얻습니다.

요약하면, 부하의 전류가 공칭값인 50mA 근처에서 변동하더라도 2mA 에서 100mA까지의 범위에서 소자의 전압은 V L =5V 로 안정적으로 유지됩니다.

게르마늄 다이오드 대 실리콘 카바이드 다이오드
그림 8에 표시된 회로도에서 D 1 과 D 2 는 각각 게르마늄과 실리콘 카바이드 다이오드입니다. 이 시리즈는 전압 V 0 = 50 V 를 공급하는 배터리로 구동됩니다. V z 는 다이오드 D 2 의 제너 전압이며 , 작동 온도 T = 400 K와 역 포화 전류 D 2 가 다이오드 D 1 의 40배라고 가정합니다 .
다음 두 가지로 나뉜 문제를 풀어야 한다고 가정해 보겠습니다.
- V z > V 0 인 경우 다이오드 양단의 전압을 결정하십시오.
- V z < V 0 이면 , 이 다이오드가 소모할 수 있는 최대 전력이 1와트, 역포화 전류가 1 µA, 동적 저항이 r=60Ω일 때 , D 1을 파괴하지 않고 V 0 −V z가 가질 수 있는 최대 값은 얼마입니까?

질문 1에 대한 솔루션
전압과 관련해서 가변적인 양( v, v 1 , v 2 , ... )을 나타낼 때는 소문자를 사용하고, 일정한 양은 대문자를 사용합니다.
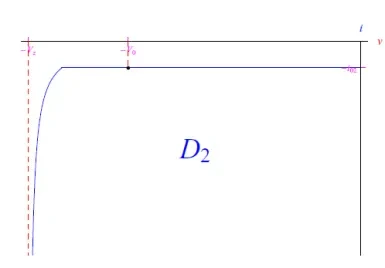
이를 감안하면 전압-전류 특성을 사용하여 솔루션을 찾을 것입니다. 다이오드 D 2 는 역전압 모드에 있으며 그 동작은 그림 9에 나와 있습니다. 이 다이오드는 발전기가 D 2 의 역포화 전류와 같은 전류 세기를 전달하도록 강제합니다. 이를 i 02 로 표시합니다 . 다이오드 D 1 을 교차하면 이 전류는 전압 강하 V 1 을 발생시키고 이는 그림 10에 나와 있는 D 1 의 전압-전류 특성을 사용하여 결정할 수 있으며 다음과 같습니다.


방정식(12)에서 다음과 같이 쓸 수 있습니다.
키르히호프의 제2법칙에 따르면 다음이 성립합니다.

질문 2에 대한 솔루션
그림 11에서 볼 수 있듯이 이 경우에는 V 0 > V z 입니다 .

키르히호프의 제2법칙을 고려하면 D 1 의 전압 강하는 V 1 =∆ V 입니다 . 회로에 흐르는 전류의 세기는 다음과 같이 D 1 의 전압-전류 특성에서 계산할 수 있습니다 .

다이오드 D1 에 의해 소모되는 전력은 다음과 같습니다.

그러면 우리는 다음과 같은 해결책을 얻을 수 있습니다.

요약하면, 공급 전압은 V z 보다 최대 0.40V까지 낮아질 수 있습니다 .