이전 페이지를 읽었다면 I/Q 신호가 무엇이고, 사분위수(즉, I/Q 신호 기반) 변조가 어떻게 이루어지는지 알 것입니다. 이 페이지에서는 진폭, 주파수 및 위상 변조된 파형에서 정보를 추출하는 다재다능한 기술인 사분위수 변조 해제에 대해 설명 합니다.
I와 Q로 변환
다음 다이어그램은 구적 복조기의 기본 구조를 보여줍니다.

이 시스템은 역방향의 사분위 변조기와 유사하다는 것을 쉽게 알 수 있습니다. RF 신호는 로컬 오실레이터 신호(I 채널용)에 곱해지고 로컬 오실레이터는 90° 이동됩니다(Q 채널용). 결과(곧 설명할 저역 통과 필터링 후)는 추가 처리를 위해 준비된 I 및 Q 파형입니다.
사분위 변조에서 우리는 기저대역 I/Q 신호를 사용하여 증폭되고 전송될 진폭, 주파수 또는 위상 변조된 파형을 생성합니다. 사분위 복조에서 우리는 기존 변조를 해당 I/Q 기저대역 신호로 변환합니다. 수신된 신호가 모든 종류의 송신기에서 나올 수 있다는 것을 이해하는 것이 중요합니다. 사분위 복조는 원래 사분위 변조를 통해 생성된 신호에 국한되지 않습니다.
저역 통과 필터는 수신 신호에 적용된 사분위수 곱셈이 예를 들어 일반적인 AM 복조기 에서 사용된 곱셈과 다르지 않기 때문에 필요합니다. 수신 스펙트럼은 캐리어 주파수(f C ) 에 의해 위아래로 이동합니다 . 따라서 2f C 를 중심으로 하는 스펙트럼과 관련된 고주파 콘텐츠를 억제하기 위해 저역 통과 필터가 필요합니다 .
진폭 복조에 대한 페이지를 읽었다면, 앞의 문단에서 사분위 복조기가 실제로 두 개의 진폭 복조기로 구성되어 있다는 것을 깨달았을 것입니다. 물론, 주파수 변조 신호에 일반적인 진폭 복조를 적용할 수는 없습니다. FM 신호의 진폭에는 인코딩된 정보가 없습니다. 하지만 사분위(진폭) 복조는 주파수 인코딩된 정보를 캡처 할 수 있습니다 . 이는 단순히 I/Q 신호의 (다소 흥미로운) 특성입니다. 위상차가 90°인 캐리어 주파수 사인파로 구동되는 두 개의 진폭 복조기를 사용하여 수신된 신호의 주파수 또는 위상의 변화를 통해 인코딩된 정보를 함께 전달할 수 있는 두 개의 다른 기저대역 신호를 생성합니다.
사분위 진폭 복조
이 장의 첫 번째 페이지인 AM 파형 복조 방법 에서 언급했듯이 진폭 복조에 대한 한 가지 접근 방식은 수신된 신호를 캐리어 주파수 기준 신호로 곱한 다음 이 곱셈의 결과를 저역 통과 필터링하는 것을 포함합니다. 이 방법은 누설 피크 검출기를 중심으로 구축된 AM 복조보다 더 높은 성능을 제공합니다. 그러나 이 접근 방식에는 심각한 약점이 있습니다. 곱셈의 결과는 송신기의 캐리어와 수신기의 캐리어 주파수 기준 신호 간의 위상 관계에 영향을 받습니다.

이 플롯은 송신기-수신기 위상차의 세 가지 값에 대한 복조된 신호를 보여줍니다. 위상차가 증가함에 따라 복조된 신호의 진폭은 감소합니다. 복조 절차는 90° 위상차에서 작동하지 않게 되었습니다. 이는 최악의 시나리오를 나타냅니다. 즉, 위상차가 90°에서 멀어짐에 따라(어느 방향으로든) 진폭이 다시 증가하기 시작합니다.
이 상황을 해결하는 한 가지 방법은 수신기의 기준 신호의 위상을 수신 신호의 위상과 동기화하는 추가 회로를 사용하는 것입니다. 그러나 쿼드러처 복조를 사용하여 송신기와 수신기 간의 동기화 부족을 극복할 수 있습니다. 방금 지적했듯이 최악의 위상 불일치는 ±90°입니다. 따라서 위상이 90°로 분리된 두 기준 신호로 곱셈을 수행하면 한 곱셈기의 출력이 다른 곱셈기의 출력의 감소하는 진폭을 보상합니다. 이 시나리오에서 최악의 위상 차이는 45°이고 위의 플롯에서 45° 위상 차이가 복조된 신호의 진폭을 크게 감소시키지 않는다는 것을 알 수 있습니다.
다음 플롯은 이 I/Q 보상을 보여줍니다. 트레이스는 사분위 복조기의 I 및 Q 분기에서 복조된 신호입니다.
송신기 위상 = 0°

송신기 위상 = 45°
(주황색 추적은 파란색 추적 뒤에 있습니다. 즉, 두 신호가 동일합니다)

송신기 위상 = 90°

상수 진폭
변조된 신호의 I 및 Q 버전을 송신기와 수신기의 위상 관계에 관계없이 일정한 진폭을 유지하는 하나의 파형으로 결합할 수 있다면 편리할 것입니다. 첫 번째 본능은 덧셈을 사용하는 것이지만 불행히도 그렇게 간단하지 않습니다. 다음 플롯은 송신기의 캐리어 위상을 제외하고는 모든 것이 동일한 시뮬레이션을 반복하여 생성되었습니다. 위상 값은 0°, 30°, 60°, 90°, 120°, 150° 및 180°의 7가지 고유한 값을 갖는 매개변수에 할당됩니다. 트레이스는 변조된 I 파형과 변조된 Q 파형의 합계입니다.

보시다시피, 덧셈은 송신기-수신기 위상 관계의 변화에 영향을 받지 않는 신호를 생성하는 방법이 아닙니다. I/Q 신호와 복소수 사이의 수학적 동등성을 기억한다면 이는 놀라운 일이 아닙니다. 신호의 I 및 Q 구성 요소는 복소수의 실수 및 허수 부분과 유사합니다. 사분위상 복조를 수행하면 기저대역 신호의 크기와 위상에 해당하는 실수 및 허수 구성 요소를 얻습니다. 즉, I/Q 복조는 본질적으로 변환 입니다 . 크기-더-위상 시스템(일반적인 기저대역 파형에서 사용)에서 I 구성 요소가 x축에 표시되고 Q 구성 요소가 y축에 표시되는 데카르트 시스템으로 변환합니다.
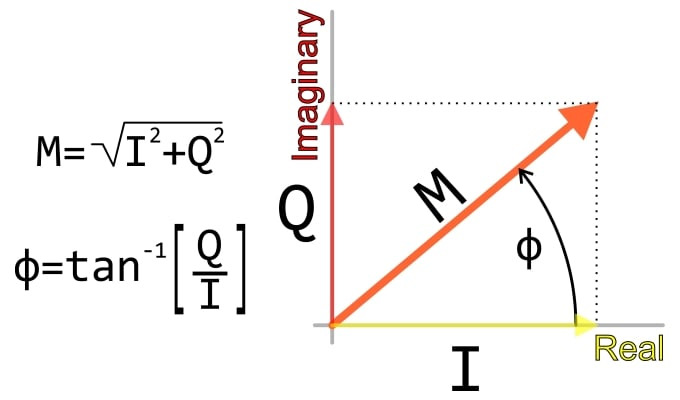
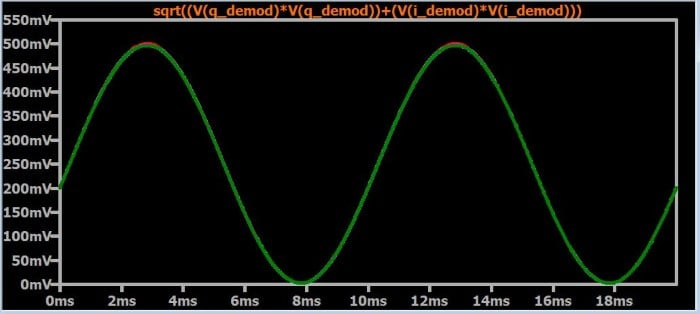
복소수의 크기를 구하기 위해 실수부와 허수부를 그냥 더할 수는 없고, I 및 Q 신호 구성 요소에도 마찬가지입니다. 대신 다이어그램에 표시된 공식을 사용해야 하는데, 이는 직각 삼각형의 빗변의 길이를 구하는 표준 피타고라스 접근 방식에 불과합니다. 이 공식을 I 및 Q 복조 파형에 적용하면 위상 변화의 영향을 받지 않는 최종 복조 신호를 얻을 수 있습니다. 다음 플롯은 이를 확인합니다. 시뮬레이션은 이전 시뮬레이션과 동일하지만(즉, 7개의 다른 위상 값) 모든 트레이스가 동일하기 때문에 신호가 하나만 보입니다.
요약
- 사분면 복조는 위상이 90°로 분리된 두 개의 기준 신호와 두 개의 곱셈기, 두 개의 저역 통과 필터를 사용하여 I 및 Q 복조 파형을 생성합니다.
- 구적 복조는 송신기와 수신기 사이의 위상 동기화가 부족한 상황에서도 호환되는 AM 복조기를 만드는 데 사용될 수 있습니다.
- 구적 복조로 인한 I 및 Q 파형은 복소수의 실수부와 허수부와 동일합니다.