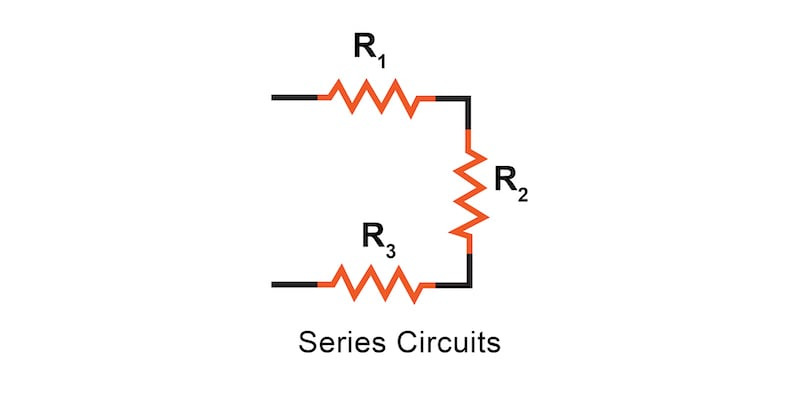
직렬 회로의 전체 저항과 전압은 얼마입니까?
직렬 회로에서 모든 구성 요소는 종단간 연결되어 전류 흐름에 대한 단일 경로를 형성합니다. 직렬 회로의 총 저항은 개별 저항의 합과 같고 총 전압 강하는 해당 저항의 개별 전압 강하의 합과 같습니다.
이 직렬 저항 회로 소개에서는 이해해야 할 세 가지 핵심 원리를 설명합니다.
- 전류: 직렬 회로의 각 구성 요소를 통과하는 전류는 동일합니다.
- 저항: 직렬 회로의 전체 저항은 개별 저항의 합과 같습니다.
- 전압: 직렬 회로의 전체 전압 강하는 개별 전압 강하의 합과 같습니다.
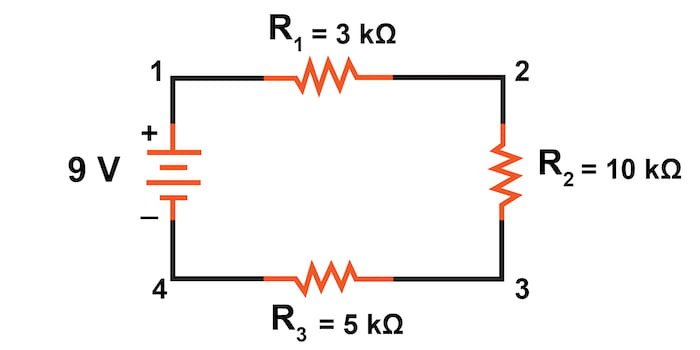
그림 1에서 설명한 것처럼, 3개의 저항과 1개의 배터리로 구성된 직렬 회로를 사용하여 이러한 세 가지 원리를 살펴보겠습니다 .
직렬 회로의 전류
직렬 회로에서 회로의 각 구성 요소를 통해 동일한 양의 전류가 흐릅니다. 이는 전류 흐름에 대한 경로가 하나뿐이기 때문입니다. 전하가 튜브의 구슬과 같은 도체를 통해 흐르기 때문에 특정 시점에서 회로(튜브)의 모든 지점에서 흐름 속도(구슬 속도)는 동일해야 합니다.
옴의 법칙 에 대한 중요한 단서 는 모든 양(전압, 전류, 저항 및 전력)이 회로의 동일한 두 지점에 따라 서로 관련되어야 한다는 것입니다. 그림 1의 더 복잡한 직렬 회로를 살펴보기 전에 단일 저항 회로에 대한 이 개념을 살펴보겠습니다.
단일 저항 회로에서 옴의 법칙 사용
이러한 초기 분석을 위해, 그림 2의 단일 저항 회로에 대한 전류와 전압을 평가할 것입니다.
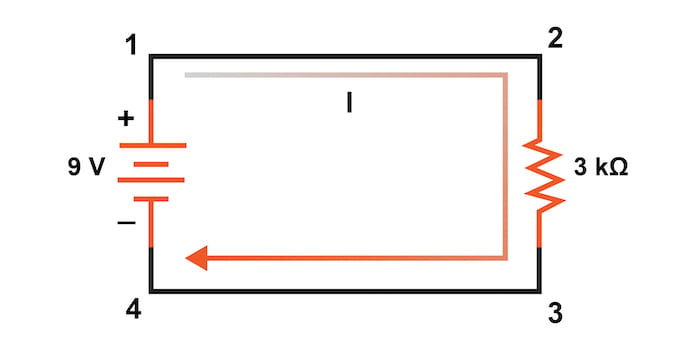
점 1과 2는 저항이 무시할 수 있는 전선으로 연결되어 있고, 점 3과 4도 마찬가지이므로 점 1은 점 2와 전기적으로 공통이고, 점 3은 점 4와 전기적으로 공통이라고 할 수 있습니다.
회로는 1점과 4점(배터리를 가로질러) 사이에 9V의 기전력을 가지고 있으므로, 2점과 3점(저항을 가로질러) 사이에도 9V를 떨어뜨려야 합니다. 이는 키르히호프의 전압 법칙 에 따르면 루프의 모든 전압의 합은 0이어야 하기 때문입니다.
따라서 우리는 저항기 전압(V)과 저항기 저항(R)을 알고 있기 때문에 저항기를 통과하는 전류에 옴의 법칙 (I = V/R)을 적용할 수 있습니다. 모든 항(V, I, R)은 회로의 동일한 두 지점과 해당 저항기에 적용되므로 아무런 예약 없이 옴의 법칙 공식을 사용할 수 있습니다.
I=VR
I=9 V3 kΩ=3 mA
여러 저항기가 있는 직렬 회로에 옴의 법칙 사용
그림 1의 회로로 돌아가면, 9V 배터리의 극성이 다시 전류 I를 발생시키고, 이 전류는 시계 방향으로 1점에서 2점, 3점, 4점으로 흐르고 다시 1점으로 돌아옵니다. 이 개념은 그림 3에 설명되어 있습니다.
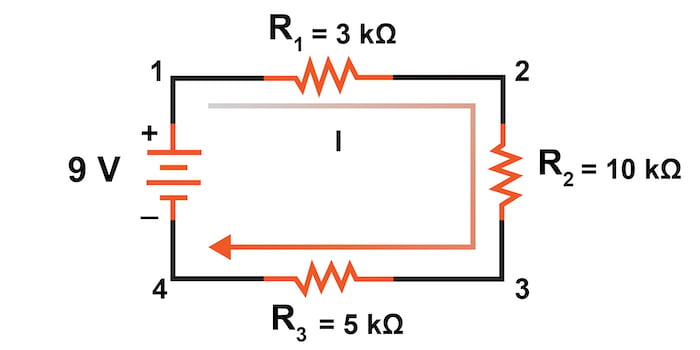
하지만 전압원은 하나이고 저항은 세 개입니다. 거기서 우리는 옴의 법칙을 어떻게 사용하는지 생각해 볼 수 있습니다.
그림 3의 3개 저항 회로 예에서, 우리는 점 1과 4 사이에 9V를 가지고 있는데, 이는 R 1 , R 2 , R 3 의 직렬 조합을 통해 전류를 구동하는 기전력의 양입니다 . 그러나 우리는 9V의 값을 취하고 3kΩ, 10kΩ 또는 5kΩ로 나누어 전류 값을 찾을 수 없습니다. 왜냐하면 우리는 각 저항기 각각에 얼마만큼의 전압이 있는지 알 수 없기 때문입니다.
9V의 전압 값은 전체 회로의 총량인 반면, 3kΩ, 10kΩ 또는 5kΩ의 값은 개별 저항기의 개별적인 양입니다. 개별 저항의 값을 가진 옴의 법칙 방정식에 총 전압의 값을 넣으면 그 결과는 실제 회로의 어떤 양과도 정확하게 연관되지 않습니다.
R 1 의 경우, 옴의 법칙은 R 1 의 저항이 3kΩ 일 때 R 1 에 걸리는 전압의 양과 R 1 에 걸리는 전류 의 양을 연관시킵니다 .
IR1=VR13 kΩ
ER1=IR1⋅3 kΩ
그러나 우리는 R1의 전압을 알지 못하고(3개 저항 직렬 조합에서 배터리가 공급하는 총 전압만) R 1을 통과하는 전류도 모르기 때문에 두 공식으로 계산을 할 수 없습니다. R 2 와 R 3 도 마찬가지입니다. 모든 항이 회로의 같은 두 지점 사이에서 각각의 양을 나타내는 경우에만 옴의 법칙 방정식을 적용할 수 있습니다.
그러면 우리는 무엇을 할 수 있을까요? 우리는 R 1 , R 2 , R 3 의 직렬 조합에 적용되는 소스(9V)의 전압을 알고 있으며 , 각 저항의 저항을 알고 있습니다. 그러나 이러한 양은 동일한 맥락에 있지 않기 때문에 옴의 법칙을 사용하여 회로 전류를 결정할 수 없습니다.
회로의 전체 저항이 무엇인지 알았다면 전체 전압(I = V/R)에 대한 값으로 전체 전류를 계산할 수 있었을 것입니다.
직렬 회로에서 총 저항을 계산하는 방법
여기서 직렬 회로의 두 번째 원리가 나옵니다. 직렬 회로의 전체 저항은 개별 저항의 합과 같습니다.
이는 직관적으로 이해가 될 것입니다. 기본적으로 전류가 흐르도록 직렬로 연결된 저항이 많을수록 전류가 흐르기 어려워집니다.
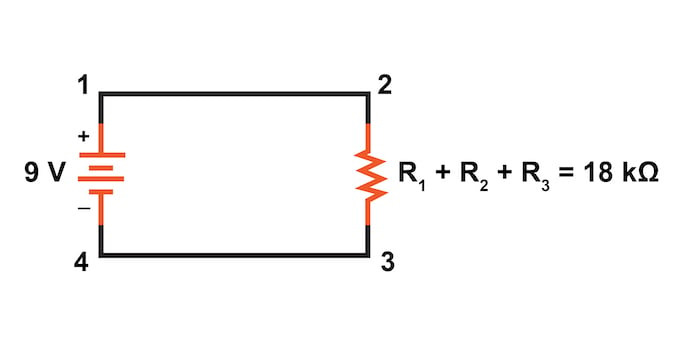
예제 문제에서 우리는 3kΩ, 10kΩ, 5kΩ 저항기를 직렬로 연결하여 총 저항을 18kΩ로 만들었습니다.
Rtotal=R1+R2+R3
Rtotal=3 kΩ+10 kΩ+5 kΩ
Rtotal=18 kΩ
본질적으로, 우리는 R 1 , R 2 , R 3 의 총 등가 저항을 합산했습니다 . 이를 알면, R 1 , R 2 , R 3 의 직렬 조합을 나타내는 단일 등가 저항으로 회로(그림 4)를 다시 그릴 수 있습니다 .
직렬 회로의 회로 전류를 계산하기 위해 옴의 법칙 사용
모든 계산이 완료되면 이제 지점 1과 4 사이의 전압(9V)과 지점 1과 4 사이의 저항(18kΩ)이 있으므로 그림 4의 회로 전류를 계산하는 데 필요한 모든 정보를 갖게 됩니다.
Itotal=VtotalRtotal
Itotal=9 V18 kΩ=500 μA
직렬 회로에서 전압 강하를 계산하는 방법
직렬 회로의 모든 구성 요소를 통과하는 전류가 동일하다는 것을 알고 있고(그리고 우리는 방금 배터리를 통과하는 전류를 결정했습니다) 그림 1의 원래 회로도로 돌아가서 그림 5에 표시된 각 구성 요소를 통과하는 전류를 다음과 같이 기록할 수 있습니다.
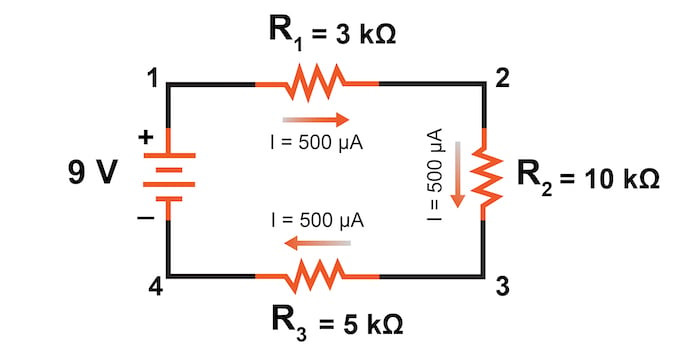
이제 각 저항기를 통과하는 전류량을 알았으므로 옴의 법칙을 사용하여 각 저항기에서의 전압 강하를 결정할 수 있습니다(옴의 법칙을 적절한 맥락에 적용).
VR1=IR1⋅R1=(500 μA)⋅(3 kΩ)=1.5 V
VR2=IR2⋅R2=(500 μA)⋅(10 kΩ)=5.0 V
VR3=IR3⋅R3=(500 μA)⋅(5 kΩ)=2.5 V
전압 강하의 합(1.5 + 5.0 + 2.5 = 9.0V)은 배터리(공급) 전압 9V와 같습니다.
이것이 직렬 회로의 세 번째 원리입니다. 직렬 회로의 전체 전압 강하는 개별 전압 강하의 합과 같습니다.
시리즈 회로 기본 리뷰:
- 직렬 회로의 모든 구성 요소는 동일한 전류를 전달합니다. I total = I 1 = I 2 = . . . I n
- 직렬 회로의 총 등가 저항은 개별 저항의 합과 같습니다. R total = R 1 + R 2 + . . . R n
- 직렬 회로의 총 전압 강하는 개별 전압 강하의 합과 같습니다. V total = V 1 + V 2 + . . . V n