키르히호프의 전류 법칙이란 무엇인가?
키르히호프의 전류 법칙은 종종 KCL로 줄여서 부르는데, "노드로 들어오고 나가는 모든 전류의 대수 합은 0이어야 한다"고 명시합니다.
이 법칙은 전하가 전선의 접속점이나 노드에 어떻게 들어오고 나가는지 설명하는 데 사용됩니다.
이러한 정보를 바탕으로 이제 실제 법률의 예를 살펴보겠습니다. 왜 그것이 중요한지, 그리고 어떻게 도출되었는지 알아보겠습니다.
병렬 회로 검토
마지막 병렬 예제 회로를 자세히 살펴보겠습니다.
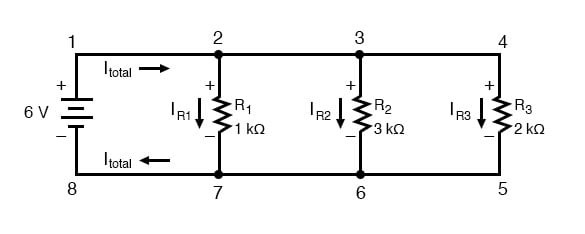
이 회로의 모든 전압과 전류 값을 풀면 다음과 같습니다.

이 시점에서 우리는 각 분기 전류의 값과 회로의 총 전류의 값을 알고 있습니다. 우리는 병렬 회로 의 총 전류가 분기 전류의 합과 같아야 한다는 것을 알고 있지만, 이 회로에는 그 이상의 일이 일어나고 있습니다. 회로의 각 와이어 접합점(노드)에서 전류를 살펴보면 다른 것을 볼 수 있어야 합니다.
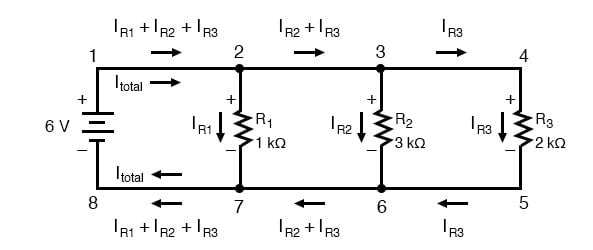
노드에 들어오고 나가는 전류
양의 "레일"(와이어 1-2-3-4)의 각 노드에서 우리는 각 연속적인 분기 저항으로 가는 주 흐름에서 전류가 분리되는 것을 봅니다. 음의 "레일"(와이어 8-7-6-5)의 각 노드에서 우리는 각 연속적인 분기 저항 에서 주 흐름을 형성하기 위해 합쳐지는 전류가 있습니다 . 모든 분기 노드가 "티" 피팅 역할을 하는 수도관 회로 비유를 생각해 보면 이 사실은 상당히 명확할 것입니다. 물 흐름은 물 펌프의 출력에서 리턴 저수조 또는 섬프 쪽으로 이동할 때 주 파이프와 분리되거나 합쳐집니다.
노드 6과 같은 특정 "티" 노드를 자세히 살펴보면 노드에 들어오는 전류의 크기가 노드에서 나가는 전류의 크기와 같음을 알 수 있습니다.
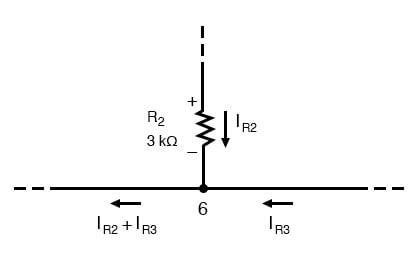
위쪽과 오른쪽에서, 노드 6으로 표시된 와이어 연결에 두 개의 전류가 들어옵니다. 왼쪽에는 노드에서 나가는 단일 전류가 있는데, 그 크기는 들어오는 두 전류의 합과 같습니다. 배관 비유를 참조하자면, 파이프에 누수가 없는 한, 피팅에 들어오는 흐름은 피팅에서도 나가야 합니다. 이는 유입 또는 유출되는 흐름의 수에 관계없이 모든 노드("피팅")에 해당합니다. 수학적으로, 우리는 이 일반적인 관계를 다음과 같이 표현할 수 있습니다.
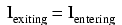
키르히호프의 전류법칙
키르히호프 씨는 이를 약간 다른 형태(수학적으로는 동일하지만)로 표현하기로 결정했으며, 이를 키르히호프 전류 법칙 (KCL)이라고 불렀습니다.

키르히호프의 전류 법칙을 한 구절로 요약하면 다음과 같습니다.
“노드에 들어오고 나가는 모든 전류의 대수 합은 0이어야 합니다.”
즉, 각 전류에 수학적 기호(극성)를 할당하여 노드에 유입(+)되는지 또는 유출(-)되는지를 표시한 다음, 이를 모두 더하면 총 0이 보장됩니다.
예시 노드(번호 6)를 사용하면 해당 전류를 알 수 없는 값으로 하는 KCL 방정식을 설정하여 왼쪽에서 나오는 전류의 크기를 결정할 수 있습니다.

5밀리암페어 값의 음수(-) 기호는 전류가 노드에서 빠져나간다 는 것을 알려주는 반면, 2밀리암페어와 3밀리암페어 전류는 둘 다 양수여야 하며(따라서 노드 로 들어옴 ) 노드에서 들어옴을 의미합니다. 음수나 양수가 전류가 들어오거나 나가는 것을 나타내는지는 전적으로 임의적이며, 반대 방향에 대한 반대 기호이고 표기법을 일관되게 유지하는 한 KCL이 작동합니다.
키르히호프의 전압 및 전류 법칙은 전기 회로를 분석하는 데 유용한 강력한 도구입니다. 그 유용성은 이후의 장(" 네트워크 분석 ")에서 더욱 분명해지겠지만, 이 법칙은 옴의 법칙 만큼이나 전자공학도가 암기해야 할 가치가 있다고만 말씀드리겠습니다 .
검토:
- 키르히호프의 전류 법칙(KCL): "노드에 들어오고 나가는 모든 전류의 대수 합은 0이어야 합니다"