메시 전류 방법을 사용하여 불균형 휘트스톤 브리지 회로 해결
불균형 휘트스톤 브리지 회로의 전류와 전압을 구하는 것은 어려울 수 있습니다. 메시 전류 방법을 사용하여 전류와 전압을 구하는 방법을 알아보세요.
불평형 휘트스톤 브리지는 저항이 복잡한 구성으로 연결되어 있기 때문에 간단한 직렬 및 병렬 회로 분석을 사용하여 해결할 수 없습니다 . 이 섹션에서는 메시 전류 방법 (루프 전류 방법이라고도 함) 을 사용하여 불평형 휘트스톤 브리지를 해결하는 방법을 보여주는 단계별 연습 과정을 제공합니다 .
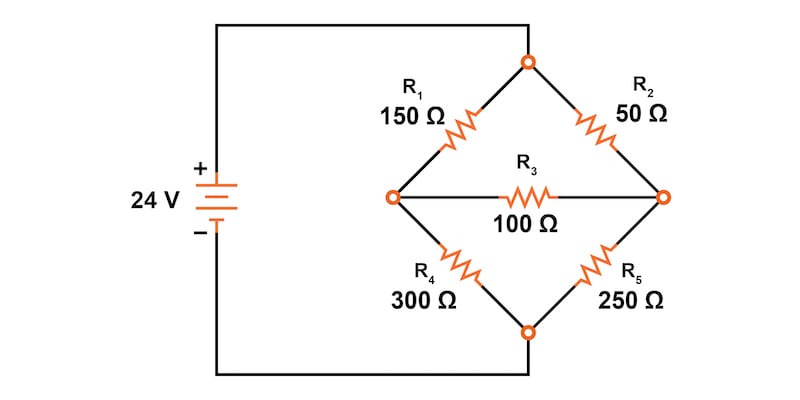
불균형 휘트스톤 브리지
먼저, 그림 1의 불평형 휘트스톤 브리지 회로에 대한 전압과 전류를 결정해 보겠습니다 .
R 1 / R 4 와 R 2 / R 5 의 비율이 같지 않기 때문에 저항기 R 3 에 전압이 걸리고 , 저항을 통과하는 전류가 어느 정도 흐릅니다. 이 장의 시작 부분에서 네트워크 분석 정리 에 대해 논의했듯이 , 이러한 유형의 회로는 일반적인 직렬-병렬 분석 으로는 환원할 수 없으며 다른 방법으로만 분석할 수 있습니다.
우리는 이 회로에 분기 전류법을 적용할 수 있지만 , 6개의 전류(I 1 ~ I 6 )가 필요하여 풀기 위해 많은 동시 방정식이 필요합니다. 반면에 메시 전류법을 사용하면 더 적은 변수로 모든 전류와 전압을 풀 수 있습니다.
메시 전류 방법의 6단계는 다음과 같습니다.
- 현재 루프를 식별하고 레이블을 지정합니다.
- 전압 강하 극성에 라벨을 붙이세요
- 각 루프에 키르히호프의 전압 법칙(KVL)을 적용합니다 .
- 알려지지 않은 전류에 대한 동시 방정식을 풀어보세요
- 메시 전류를 다시 그리며 분기 전류를 결정하십시오.
- 옴의 법칙을 사용하여 전압 강하를 계산합니다.
1단계: 현재 루프 식별 및 레이블 지정
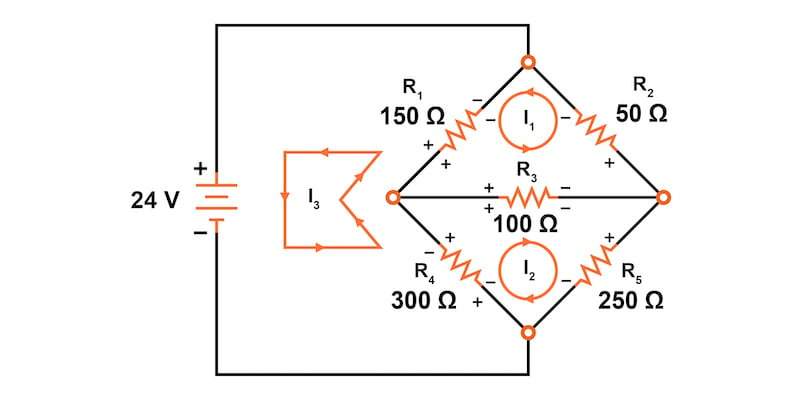
메시 전류 방법의 첫 번째 단계는 회로의 모든 구성 요소를 설명하기에 충분한 메시 전류를 그리는 것입니다. 브리지 회로를 살펴보면 그림 2에 표시된 대로 이러한 전류 루프 두 개를 어디에 배치해야 하는지 분명할 것입니다.
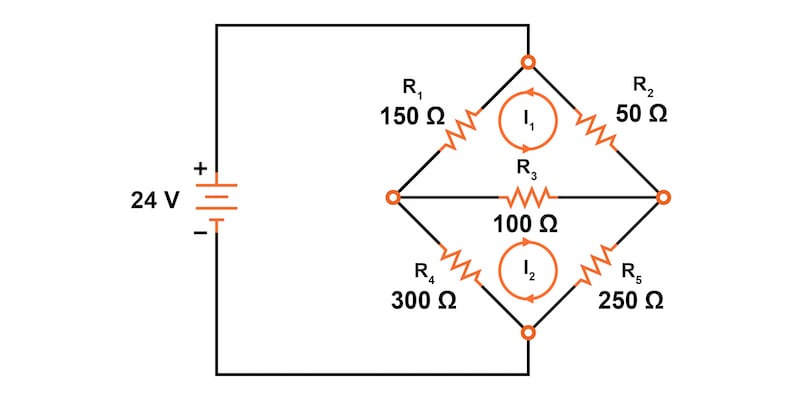
물론 이러한 메시 전류의 방향은 임의적입니다. 그러나 이 회로에서는 두 개의 메시 전류로는 충분하지 않습니다. I 1 도 I 2 도 배터리를 통과하지 않기 때문입니다. 따라서 그림 3에 나와 있듯이 세 번째 메시 전류 I 3 을 추가해야 합니다 .
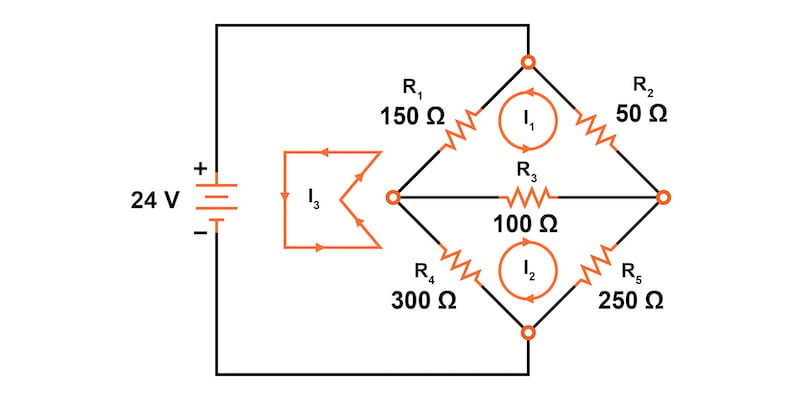
여기서 우리는 배터리의 음극 단자에서 시작하여 R 4를 거쳐 R 1을 거쳐 배터리의 양극 단자로 돌아오는 I 3을 선택했습니다. 이것은 I 3 에 대해 선택할 수 있는 많은 경로 중 하나이지만 이 예가 가장 간단해 보입니다.
2단계: 전압 강하 극성 레이블 지정
이제 각 전류 방향에 따라 저항기 전압 강하 극성을 표시해야 합니다(그림 4).
3단계: 각 루프에 Kirchhoff의 전압 법칙 적용
다음으로, 브리지의 상단 루프에 대한 KVL 방정식을 생성해 보겠습니다. 상단 노드에서 시작하여 시계 방향으로 추적합니다. 그 결과 다음과 같은 방정식이 생성됩니다.
R2I1+R3(I1+I2)+R1(I1−I3)==0 V
50I1+100(I1+I2)+150(I1−I3)=0 V
이 방정식에서 우리는 각 저항기를 통과하는 전류를 루프 전류의 대수 합으로 표현합니다. 예를 들어, 저항기 R 3 의 전압은 위의 KVL 방정식에서 100(I 1 + I 2 ) 라는 식으로 표현됩니다 . 왜냐하면 두 전류 I 1 과 I 2 가 같은 방향으로 R 3을 통과하기 때문입니다. 저항기 R 1 의 전압은 루프 전류 I 1 과 I 3 이 서로 반대이기 때문에 150(I 1 - I 3 ) 으로 표현됩니다 .
유사한 용어를 결합하면 다음과 같이 간소화할 수 있습니다.
300I1+100I2−150I3=0 V
이제, 우리는 같은 과정을 반복하여 휘트스톤 브리지의 하단 루프에 대한 KVL 방정식을 생성할 수 있습니다. 하단에서 시작하여 시계 반대 방향으로 이동해 보겠습니다.
R5I2+R3(I2+I1)+R4(I2+I3)==0 V
유사한 용어를 결합하면 다음과 같은 방정식을 얻습니다.
100I1+650I2+300I3=0 V
방정식의 원래 형태에서 두 번째 항은 저항 R 3 의 값 100 Ω에 I 2 와 I 1 의 합 (I 2 + I 1 )을 곱한 것을 주목하십시오. 이는 해당 전류가 R 3 을 통해 같은 방향으로 흐르기 때문입니다 . 저항 R 4 를 통과하는 전류 I 2 와 I 3 에도 동일하게 적용됩니다 .
그렇게 해서 이제 두 방정식을 처리했습니다. 그러나 세 변수와 세 방정식의 동시 방정식 세트를 완성하려면 세 번째 방정식이 여전히 필요합니다. 이 세 번째 방정식에는 배터리 전압도 포함되어야 하는데, 지금까지는 이전 KVL 방정식 두 개에 나타나지 않았습니다.
이 방정식을 생성하기 위해, 우리는 가상 전압계 로 다시 루프를 추적할 것입니다 . 배터리의 바닥(음극) 단자에서 시작하여 시계 방향으로 스테핑합니다. 다시 말하지만, 우리가 스테핑하는 방향은 임의적이며 해당 루프의 메시 전류 방향과 같을 필요는 없습니다.
24+R1(I3−I1)+R4(I3+I2)==0 V
다시 말해, 유사한 용어를 결합하고 방정식을 단순화하면 다음과 같습니다.
−150I1+300I2+450I3=24 V
4단계: 알려지지 않은 전류에 대한 동시 방정식 풀기
이제 우리는 우리가 선호하는 방법을 사용하여 풀 수 있는 세 개의 동시 방정식이 있습니다.
300I1+100I2−150I3=0 V
KVL of Loop 1
100I1+650I2+300I3=0 V
KVL of Loop 2
−150I1+300I2+450I3=24 V
KVL of Loop 3
우선, 우리는 오픈소스 Matlab 클론인 GNU Octave 를 사용하여 이러한 방정식을 풀 것입니다. 우리는 저항 계수를 행렬 A에 입력할 수 있습니다. 행렬 A는 대괄호로 구분된 열 요소와 세미콜론으로 구분된 행 요소로 구성됩니다.
다음으로, 우리는 전압을 열 벡터 b에 입력할 수 있습니다. 알려지지 않은 전류: I 1 , I 2 , I 3 는 다음 명령으로 계산됩니다: x = A \ b. 이러한 전류는 결과 x-열 벡터에 포함됩니다.
옥타브:1>A = [300,100,150;100,650,-300;-150,300,-450]
아 =
300 100 150
100 650 -300
-150 300 -450
옥타브:2> b = [0;0;-24]
비 =
0
0
-24
옥타브:3> x = A\b
엑스 =
-0.093793
0.077241
0.136092
따라서 루프 전류의 값은 다음과 같습니다.
- I1 = -93.793 mA
- I2 = 77.241 mA
- I3 = -136.092 mA
5단계: 메시 전류를 다시 그리며 분기 전류를 결정합니다.
전류 I 1 및 I 3 에 대한 음수 값은 우리가 가정한 전류 방향이 잘못된 방향임을 나타냅니다. I 3 의 경우 전류가 회로의 유일한 전원에서 흘러나와야 하기 때문에 직관적으로 말이 됩니다.
따라서 실제 루프 전류 방향과 방향 저항은 그림 5에 표시되어 있습니다.
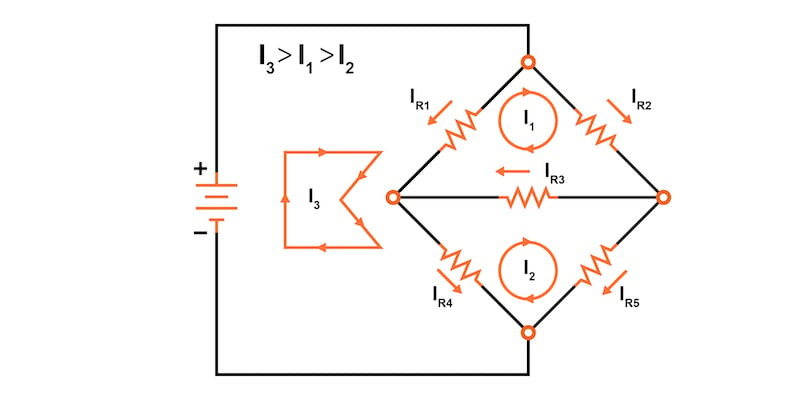
여기에서 분기 저항 전류 값을 계산할 수 있습니다.
$$I_{R1} = I_3 - I_1 = 136.092 - 93.793 = 42.299 \text{ mA}$$
$$I_{R2} = I_1 = 93.793 \text{ mA}$$
$$I_{R3} = I_1 - I_2 = 93.793 - 77.241 = 16.552 \text{ mA}$$
$$I_{R4} = I_3 - I_2 = 136.092 - 77.241 = 58.851 \text{ mA}$$
$$I_{R5} = I_2 = 77.241 \text{ mA}$$
6단계: 전압 강하 계산
마지막으로, 각 저항기에서의 전압 강하를 계산할 수 있습니다.
$$V_{R1} = I_{R1}R_1 = (0.042299) \cdot (150) = 6.3448 \text{ V}$$
$$V_{R2} = I_{R2}R_5 = (0.093793) \cdot (50) = 4.6897 \text{ V}$$
$$V_{R3} = I_{R3}R_5 = (0.016552) \cdot (100) = 1.6552 \text{ V}$$
$$V_{R4} = I_{R4}R_5 = (0.058851) \cdot (300) = 17.6553 \text{ V}$$
$$V_{R5} = I_{R5}R_5 = (0.077241) \cdot (250) = 19.3103 \text{ V}$$
SPICE를 사용하여 전압 계산 확인
다음으로, 전압 계산의 정확성을 확인하기 위해 그림 6의 회로를 사용하여 SPICE 시뮬레이션을 사용할 수 있습니다.
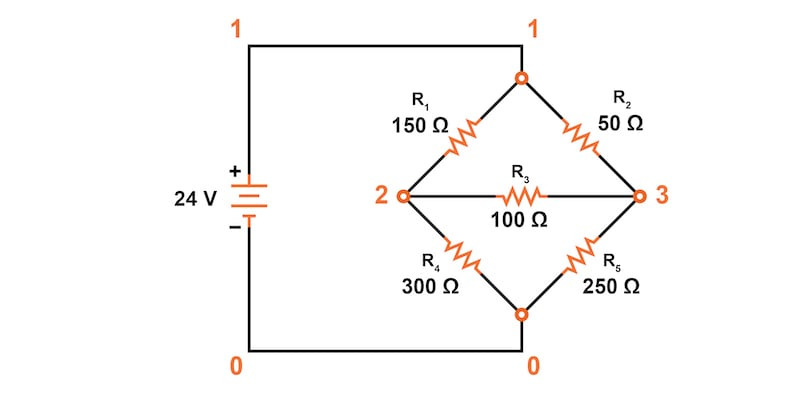
불균형 휘트스톤 브리지
v1 1 0
r1 1 2 150
r2 1 3 50
r3 2 3 100
r4 2 0 300
r5 3 0 250
.dc v1 24 24 1
.print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0)
.끝
v1 v(1,2) v(1,3) v(3,2) v(2) v(3)
2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
불균형 휘트스톤 브리지 검토를 위한 메시 전류 방법
메시 전류법을 사용하여, 우리는 불평형 휘트스톤 브리지의 전류와 전압을 풀 수 있었습니다. 세 개의 알려지지 않은 루프 전류를 가진 세 개의 동시 KVL 방정식은 GNU Octave를 사용하여 풀었습니다. 그런 다음, 우리는 SPICE 회로 시뮬레이션 소프트웨어를 사용하여 결과를 검증했습니다.ㅍ