
DC 네트워크 분석을 위한 노드 전압 방법이란 무엇입니까?
노드 전압법은 키르히호프의 전류 법칙을 구조적으로 적용한 DC 네트워크 분석 기술입니다. 이 방법은 전압원을 전류원으로 변환하고 저항을 등가 전도도로 대체하는 것을 포함합니다.
DC 네트워크 분석 의 노드 전압 방법은 키르히호프 전류 법칙(KCL) 방정식 의 시스템을 기준으로 회로 노드에서 알려지지 않은 전압을 해결합니다 . 이 분석은 전압 소스를 등가 전류 소스로 대체하기 때문에 이상하게 보입니다. 또한 옴 단위의 저항 값은 지멘스(S) 단위의 등가 컨덕턴스(G = 1/R)로 대체됩니다. 노드 전압 방법을 이해하면 다양한 복잡한 회로를 빠르게 해결하는 간단한 기술을 제공할 수 있습니다.
이 교과서 페이지에서는 불평형 휘트스톤 브리지를 포함한 두 회로에 대한 노드 전압 방법을 설명합니다 .
노드 전압 방법 단계
먼저, 그림 1에서 설명한 것과 같은 기존의 전압원을 갖춘 회로부터 살펴보겠습니다.
1단계: 모든 고유 전압 노드에 레이블 지정
공통 노드 V 0 를 참조점으로 선택합니다. 이는 일반적으로 회로의 접지 노드입니다. 그림 1 회로의 다른 알려지지 않은 노드 전압 V 1 과 V 2 는 이 지점과 관련하여 계산됩니다.

2단계: 모든 전압 소스 및 직렬 저항을 전류 소스 및 병렬 저항으로 교체
다음으로, 모든 전압 소스와 관련 직렬 저항을 등가 전류 소스와 병렬 저항 으로 교체해야 합니다 . 전류 소스 값은 다음과 같이 계산됩니다.
나에스영형유아르 자형기음이자형=다섯에스영형유아르 자형기음이자형아르 자형에스이자형아르 자형나이자형에스
그림 1의 전압원 B1 은 전류원 값이 5A인 저항기 R1 과 직렬로 연결됩니다 .
나1=다섯비1아르 자형1=10 다섯2 Ω=5 에이
병렬 저항은 직렬 저항과 같은 값이 됩니다. 전류 소스와 저항 값을 알고 있으면 그림 2와 같이 동등한 병렬 회로를 그릴 수 있습니다.

그림 1의 회로에서 직렬 저항 R5를 사용하여 배터리 B2 에 대해 동일한 전압원을 전류원으로 변환해야 합니다 .
나2=다섯비2아르 자형5=−4 다섯1 Ω=−4 에이
이제 그림 3과 같이 두 개의 전류원과 병렬 저항을 사용하여 회로를 다시 그릴 수 있습니다.

3단계: 저항기 저항(Ω)을 Siemens 전도도(Conductance)로 교체
회로의 모든 저항기 에 대해 이제 저항 값(옴)을 역수 전도도 값(지멘스)으로 대체해야 합니다. 지멘스는 전도도의 단위로, 지금은 쓸모없는 mho(옴의 역수) 단위를 대체했습니다.
G1=1아르 자형1=12 Ω=0.5 에스
G2=1아르 자형2=14 Ω=0.25 에스
G3=1아르 자형3=12.5 Ω=0.4 에스
G4=1아르 자형4=15 Ω=0.2 에스
G5=1아르 자형4=11 Ω=1 에스
우리는 계산된 전도도 값을 이용해 도면을 업데이트할 수 있습니다(그림 4).
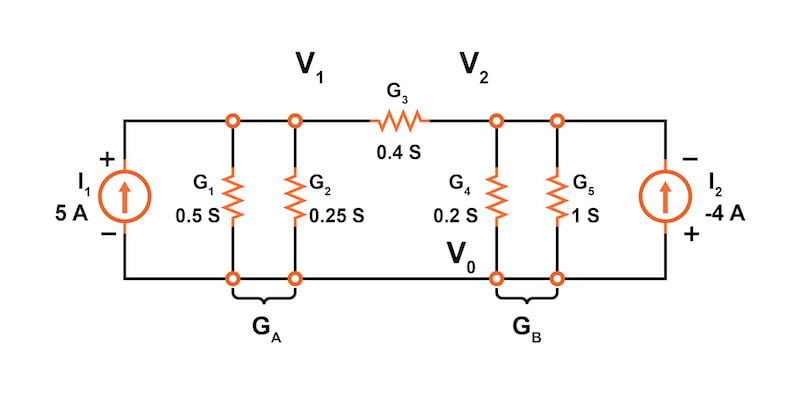
이 지점에서, 우리는 또한 병렬 도체를 결합하여 회로를 단순화할 수 있습니다. 우리는 간단한 추가로 이를 수행합니다. 그림 4의 회로에서, 우리는 두 세트의 병렬 도체를 가지고 있습니다:
G에이=G1+G2=0.5+0.25=0.75 에스
G비=G4+G5=0.2+1=1.2 에스
노드 전압법을 적용할 준비가 된 단순화된 회로가 그림 5에 나와 있습니다.

4단계: 알려지지 않은 각 전압 노드에 대한 KCL 방정식 작성
노드 전압법에 따라 이제 모든 알려지지 않은 전압 노드에 대한 KCL 방정식을 작성합니다. 예제 회로에서 알려지지 않은 노드 전압은 V 1 과 V 2 뿐입니다 .
나1=G에이다섯1+G3(다섯1−다섯2)
방정식 1.
나2=G비다섯2+G3(다섯2−다섯1)
방정식 2.
이 두 방정식을 다시 써서 이러한 방정식을 검토하여 작성하는 패턴을 보여드리겠습니다.
나1=(G에이+G3)다섯1−G3다섯2
방정식 1.
나2=(G비+G3)다섯2−G3다섯1
방정식 2.
이 두 방정식의 유사성에 주목하세요. 첫 번째 KCL 노드에 연결된 컨덕턴스의 합(GA + G3 ) 은 방정식 1에서 해당 노드의 첫 번째 전압( V1 ) 의 양의 계수입니다. 마찬가지로 방정식 2에서 V2 에 대한 해당 KCL 노드에 연결된 컨덕턴스의 합은 방정식 2 의 전압 V2의 양의 계수입니다. 다른 계수는 음수로 다른 비공통 노드 간의 컨덕턴스를 나타냅니다.
두 방정식 모두에서 왼쪽은 노드에 연결된 각각의 전류원과 같습니다. 이 패턴을 사용하면 검사하여 방정식을 빠르게 작성할 수 있습니다. 컨덕턴스를 사용하여 KCL 방정식을 작성하는 이 비교적 간단한 패턴을 배울 수 있다면 노드 전압 방법은 많은 회로를 빠르게 분석하는 데 유용할 수 있습니다.
5단계: 미지 전압에 대한 동시 KCL 방정식 집합 풀기
여기에서, 우리는 두 방정식을 사용하여 회로의 두 개의 알려지지 않은 전압을 풀 수 있습니다. 우리는 알려진 전류와 전도도를 대입하여 유사한 용어로 다시 정렬할 수 있습니다.
나1=5=(0.75+0.4)다섯1−0.4다섯2=1.15다섯1−0.4다섯2
나2=−4=(1.2+0.4)다섯2−0.4다섯1=−0.4다섯1+1.6다섯2
이러한 동시 방정식을 풀면 노드 전압에 대한 다음과 같은 결과를 얻습니다.
다섯1=3.8095 다섯
다섯2=−1.5476 다섯
SPICE를 이용한 노드 전압 방법 검증
그런 다음 전압 소스가 있는 원래의 회로도를 기반으로 SPICE를 사용하여 솔루션을 검증할 수 있습니다. 그러나 전류 소스가 있는 회로도도 시뮬레이션할 수 있었습니다.
* 노드 전압법 회로 시뮬레이션
V1 11 0 DC 10
V2 22 0 DC -4
r1 11 1 2
r2 1 0 4
r3 1 2 2.5
r4 2 0 5
r5 2 22 1
.DC V1 10 10 1 V2 -4 -4 1
.DC V(1) V(2)를 출력하세요
.끝
v(1) v(2)
3.809524e+00 -1.547619e+00
불평형 휘트스톤 브리지에 적용된 노드 전압 방법
노드 전압 방법을 사용한 또 다른 회로 분석 예를 살펴보겠습니다. 그림 6의 회로는 불평형 휘트스톤 브리지라고 하며, 세 개의 알려지지 않은 전압 노드와 공통 전압 노드 V 0 를 갖습니다 .

회로도에 전도도를 나열하지 않는다는 점에 유의하는 것이 중요합니다. 그러나 G 1 = 1/R 1 등입니다.
검사로 방정식을 쓸 노드는 세 개(V 1 , V 2 , V 3 ) 가 있습니다 . 기억하세요, 전도 계수는 우리가 KCL 방정식을 개발하고 있는 노드에 연결된 도체의 경우 양수입니다. 다른 모든 전도 계수는 음수입니다.
다이어그램에 있는 저항기의 전도도를 계산하기에는 너무 게으르기 때문에, 아래 첨자로 표시된 G는 일단 계수로 나열됩니다.
나1=0.136092=(G1+G2)다섯1−G1다섯2−G2다섯3
나2=0=(G1+G3+G4)다섯2−G1다섯1−G3다섯3
나3=0=(G2+G3+G5)다섯3−G2다섯1−G3다섯2
다음으로, 우리는 동시 방정식을 풀기 쉽게 하기 위해 알려지지 않은 전압을 정렬하기 위해 재정렬할 수 있습니다.
0.136092=(G1+G2)다섯1−G1다섯2−G2다섯3
0=−G1다섯1+(G1+G3+G4)다섯2−G3다섯3
0=−G2다섯1−G3다섯2+(G2+G3+G5)
다시 말해서, 우리는 너무 게으르기 때문에 GNU Octave를 사용하여 이 문제를 풀고 상호 저항과 상호 저항의 합을 Octave "A" 행렬에 입력하여 Octave가 "A =" 뒤에 전도도 행렬을 계산하도록 할 것입니다.
초기 입력 라인은 너무 길어서 세 개의 행으로 나뉘었습니다. 입력된 "A" 행렬은 시작 및 종료 대괄호로 구분됩니다. 열 요소는 공백으로 구분됩니다. 행은 "줄바꿈"으로 구분됩니다. 구분 기호로 쉼표와 세미콜론은 필요하지 않습니다. 그러나 "b"의 전류 벡터는 세미콜론으로 구분되어 전류의 열 벡터가 생성됩니다.
옥타브:12> A = [1/150+1/50 -1/150 -1/50
> -1/150 1/150+1/100+1/300 -1/100
> -1/50 -1/100 1/50+1/100+1/250]
아 =
0.0266667 -0.0066667 -0.0200000
-0.0066667 0.0200000 -0.0100000
-0.0200000 -0.0100000 0.0340000
옥타브:13> b = [0.136092;0;0]
비 =
0.13609
0.00000
0.00000
옥타브:14> x=A\b
엑스 =
24.000
17,655명
19.310
"A" 행렬의 대각선 계수는 양수이고 다른 계수는 모두 음수입니다. 이는 노드 전압 방법 방정식을 작성하기 위한 규칙에 따라야 하기 때문입니다.
전압 벡터 솔루션은 "x"에 제공됩니다.
- V1 = 24.000V
- V2 = 17.655V입니다 .
- V3 = 19.310V
이 세 가지 전압은 우리가 불평형 휘트스톤 브리지의 메시 전류 분석과 SPICE 시뮬레이션을 사용하여 얻은 결과와 동일합니다. 이는 우연이 아닙니다. 0.13609 A 전류 소스는 해당 문제에서 전압 소스로 사용된 24V를 산출하기 위해 의도적으로 선택되었습니다.
노드 전압 방법 검토
- 노드 전압법은 모든 전압원을 전류원으로, 저항을 전도도로 대체한 후 키르히호프의 전류 법칙을 구조적으로 적용한 회로 분석 기법입니다.
- 노드 전압 방법은 5단계 프로세스를 따릅니다.
- 1단계: 참조 노드(일반적으로 접지)를 선택한 후 모든 고유 전압 노드에 레이블을 지정합니다.
- 2단계: 모든 전압 소스와 직렬 저항기를 전류 소스와 병렬 저항기로 교체합니다.
- 3단계: 저항기 저항(옴)을 지멘스 전도도(시멘스)로 교체
- 4단계: 알 수 없는 각 전압 노드에 대한 KCL 방정식 작성
- 5단계: 알 수 없는 전압에 대한 동시 KCL 방정식 집합을 풀어보세요.
- 4단계에서 KCL 방정식을 작성할 때, 검토를 통해 이를 작성할 수 있습니다.
- 첫 번째 방정식에서 첫 번째 전압의 양수 계수는 노드에 연결된 전도도의 합입니다. 두 번째 방정식에서 두 번째 전압의 계수는 해당 노드에 연결된 전도도의 합입니다. 세 번째 전압, 세 번째 방정식 및 다른 방정식의 계수에 대해 반복합니다.
- 모든 방정식의 다른 모든 계수는 KCL 평가에 따른 전압 노드에서 다른 모든 노드로의 전도도를 나타내는 음수입니다. 첫 번째 방정식에서 두 번째 계수는 노드 1에서 노드 2까지의 전도도이고, 세 번째 계수는 노드 1에서 노드 3까지의 전도도입니다. 다른 방정식의 경우 음수 계수를 채우십시오.
- KCL 방정식의 다른 측면은 각 노드에 연결된 전류원입니다.