
회로 분석에서 노튼의 정리란 무엇입니까?
노튼의 정리는 모든 선형 회로가 단일 전류원과 부하에 연결된 병렬 저항으로 구성된 등가 회로로 단순화될 수 있다고 말합니다.
이 문서에서는 노턴 등가 회로와 노턴 정리를 결정하는 단계별 프로세스를 설명합니다 . 노턴 정리는 모든 선형 회로를 등가 회로로 단순화할 수 있다는 점에서 테브난 정리 와 유사합니다. 그러나 전압원 과 직렬 저항을 사용하는 대신 노턴 등가 회로는 병렬 저항이 있는 전류원 으로 구성됩니다 . 노턴 정리를 적용하여 네트워크를 단순화하면 가변 부하를 훨씬 더 쉽게 평가할 수 있습니다.
선형 회로에 노튼 정리 적용하기
테브난 정리와 중첩 정리와 마찬가지로, 노튼 정리는 모든 기본 방정식에 지수나 근이 포함되지 않는 선형 회로에서만 사용할 수 있습니다. 회로는 저항기 , 인덕터 , 커패시터 와 같은 표준 수동 구성 요소 만 사용하는 경우 선형입니다 . 게다가 대부분의 전압원, 배터리, 전류원도 선형입니다.
자세히 살펴보면서, 우리가 다른 많은 네트워크 분석 방법을 설명하는 데 사용하는 것과 동일한 예제 회로(그림 1)를 사용하여 노턴의 정리를 설명해보겠습니다. 여기에는 다음이 포함됩니다.
이렇게 하면 다양한 방법을 더 쉽게 비교할 수 있습니다.

노턴 등가 회로란 무엇입니까?
노튼의 정리를 사용하면 그림 1의 원래 회로에서 부하 저항을 일시적으로 제거하고 남은 회로를 단일 전류원과 병렬 저항으로 구성된 등가 회로로 줄일 수 있습니다.
다음으로, 부하 저항을 노턴 등가 회로에 다시 연결하여 전체 네트워크가 간단한 병렬 회로 인 것처럼 계산할 수 있습니다 .
노턴 변환을 거치면 그림 1의 회로는 그림 2의 노턴 등가 회로로 축소됩니다.

전류원이란 일정한 양의 전류를 공급하고, 그 일정한 전류를 유지하는 데 필요한 만큼의 전압을 출력하는 것이 목적인 부품입니다.
노턴 등가 회로 계산 - 노턴 전류 및 노턴 저항
테브난 정리와 마찬가지로 원래 회로에서 부하 저항을 제외한 모든 것이 분석하기 더 간단한 등가 회로로 축소되었습니다. 테브난 정리와 마찬가지로 노턴 정리에서 노턴 소스 전류(I Norton )와 노턴 저항(R Norton )을 계산하는 데 사용되는 단계는 일반적으로 유사합니다.
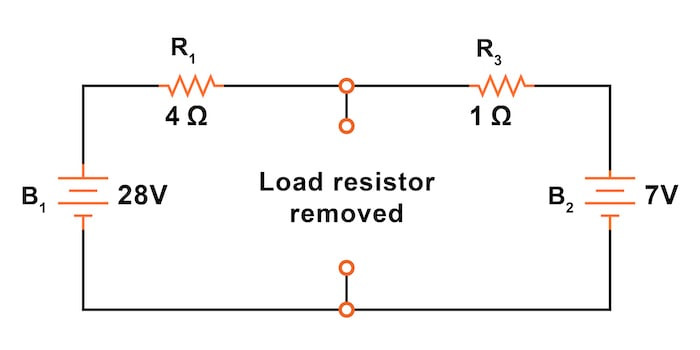
1단계: 부하 저항 제거
첫 번째 단계는 부하 저항을 식별하고 그림 3과 같이 원래 회로에서 제거하는 것입니다.
2단계: Norton Current 계산
노턴 전류(노턴 등가 회로의 전류원)를 구하려면 부하 지점 사이에 직접선(단락 회로) 연결을 하고 합성 전류를 결정합니다(그림 4).

이 단계는 테브난 정리에서 부하 저항을 브레이크(개방 회로)로 대체하여 전압을 계산한 단계와 반대입니다.
그림의 회로에 대한 현재 계산은 R 1 과 R 3 사이의 노드가 이제 두 배터리의 음극 단자에 단락되었기 때문에 비교적 간단합니다. 키르히호프의 전류 법칙(KCL)을 사용하면 다음을 알 수 있습니다.
Ishort=IR1+IR2
이제 각각의 분기 전류에 옴의 법칙을 적용해 보겠습니다.
Ishort=IR1+IR2=V1R1+V2R2
단락 전류를 다음과 같이 풀 수 있습니다.
INorton=Ishort=284+71=7+7=14 A
3단계: 전원 교체
등가 회로의 노턴 저항을 구하기 위해 이제 그림 3의 회로에서 전원을 그림 5와 같이 바꿀 수 있습니다.

전압원은 단락 회로로 대체되고 전류원은 개방 회로로 대체됩니다. 전원 공급 장치를 대체하는 이 프로세스는 중첩 정리와 테브난 정리에 사용된 프로세스와 동일합니다.
4단계: 노탄 저항 계산
두 전압원을 교체한 후, 제거된 부하 위치에서 측정된 총 저항은 그림 6과 같이 병렬로 연결된 R1 과 R3 와 같습니다.

노턴 등가 저항은 다음과 같이 계산됩니다.
RNorton=11R1+1R3=114+11=0.8 Ω
0.8Ω의 값은 노턴 저항(R Norton )입니다.
5단계: 노턴 등가 회로 그리기
그림 7에 표시된 단순화된 노턴 등가 회로는 이제 연결 지점 사이에 연결된 모든 선형 부하 장치를 계산하는 데 사용될 수 있습니다.

이 그림에서는 원래 회로에서 2Ω 부하 저항을 다시 부착했습니다.
노턴 등가 회로 사용
모든 단계를 거친 후, 그림 7에 표시된 노턴 회로를 분석하여 부하 저항을 통과하는 전류와 그에 따른 전압 강하를 결정할 수 있습니다. 이제 이것은 단순히 병렬로 연결된 두 개의 저항이므로 노턴 전류 소스에서 보이는 총 저항을 다음과 같이 결정할 수 있습니다.
RTotal=11RNorton+1RLoad=110.8+12=0.57143 Ω
Table Method를 사용하면 총 저항 값을 Table 1에 넣은 다음 나머지 표에 채울 수 있습니다. 부하 저항의 전류는 4.0A이고 전압 강하는 8V입니다.
표 1. 부하 전류 및 전압 강하 계산
| 8.0 | 8.0 | 8.0 | 다섯 |
| 10.0 | 4.0 | 14.0 | 에이 |
| 0.8 | 2.0 | 0.57143 | Ω |
테브난 등가 회로와 마찬가지로 이 분석에서 유일하게 유용한 정보는 부하 저항 R2의 전압과 전류 값입니다. 나머지 정보는 원래 회로와 관련이 없습니다.
그러나 테브난 정리에서 보이는 동일한 이점이 노튼 정리에도 적용됩니다. 즉, 부하 저항 전압과 전류를 여러 다른 부하 저항 값에 걸쳐 분석하고자 하는 경우 노튼 등가 회로를 반복해서 사용할 수 있으며, 각 시험 부하에서 무슨 일이 일어나는지 확인하기 위해 간단한 병렬 회로 분석보다 더 복잡한 것은 적용하지 않습니다.
노튼 정리와 노튼 등가 회로 검토
노튼의 정리는 모든 선형 회로가 단일 전류원과 부하에 병렬로 연결된 단일 저항을 갖는 등가 회로로 단순화될 수 있다고 말합니다.
- 1단계: 부하 저항을 제거하고 단락 회로로 교체합니다.
- 2단계: 노턴 전류(단락 회로를 통과하는 전류)를 계산합니다.
- 3단계: 전원 교체. 모든 전압원은 단락 회로로 교체하고, 모든 전류원은 개방 회로로 교체합니다.
- 4단계: 노턴 저항을 계산합니다. 노턴 저항은 모든 소스를 제거한 후 개방 회로 연결 지점 간의 총 저항입니다.
- 5단계: Norton 전류원을 Norton 저항과 병렬로 연결하여 Norton 등가 회로를 그립니다. 부하 저항은 등가 회로의 두 개방 지점 사이에 다시 부착됩니다.
- 병렬 회로의 규칙에 따라 부하의 전압과 전류를 분석합니다.