많은 회로 응용 분야에서 우리는 3단자 네트워크를 형성하기 위해 두 가지 방식 중 하나로 연결된 구성 요소를 만납니다. 즉, "델타" 또는 Δ(또한 "파이" 또는 π라고도 함) 구성과 "Y"(또한 "T"라고도 함) 구성입니다.

단자 연결만으로 분석한 것처럼, 한 종류의 네트워크(Δ 또는 Y)를 형성하는 데 필요한 저항기 의 적절한 값을 계산하여 다른 종류와 동일하게 동작하는 것을 확인할 수 있습니다. 즉, 두 개의 별도 저항기 네트워크, 하나는 Δ이고 하나는 Y이고, 각각 저항기가 보이지 않고 테스트를 위해 세 개의 단자(A, B, C)만 노출되어 있다면, 저항기는 두 네트워크에 맞게 크기를 조정하여 한 네트워크를 다른 네트워크와 전기적으로 구별할 방법이 없도록 할 수 있습니다. 즉, 동등한 Δ 및 Y 네트워크는 동일하게 동작합니다.
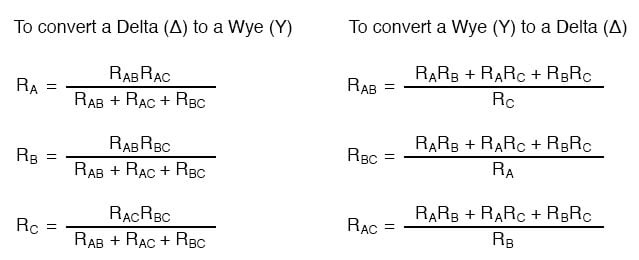
Δ 및 Y 변환 방정식
한 네트워크를 다른 네트워크로 변환하는 데 사용되는 방정식은 여러 가지가 있습니다.
Δ와 Y 네트워크는 3상 AC 전력 시스템(이 책 시리즈의 2권에서 다루는 주제)에서 자주 볼 수 있지만, 그때조차도 보통 균형 네트워크(모든 저항의 값이 같음)이고, 하나에서 다른 하나로 변환하는 데 그렇게 복잡한 계산이 필요하지 않습니다. 언제 일반 기술자가 이런 방정식을 사용해야 할까요?
Δ 및 Y 변환의 응용
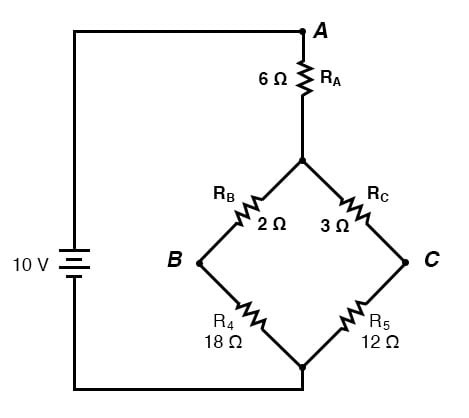
Δ-Y 변환의 주요 응용 분야는 아래와 같은 불균형 브리지 회로의 솔루션입니다.
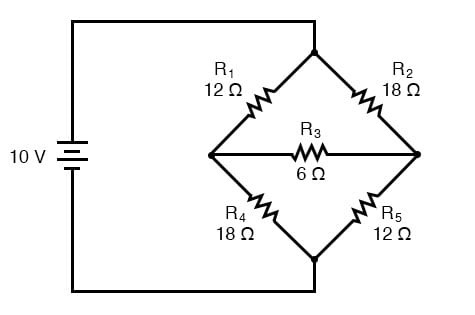
이 회로의 Branch Current 또는 Mesh Current 분석 솔루션은 상당히 복잡하고, 전력 공급원이 하나뿐이기 때문에 Millman 정리나 Superposition 정리는 도움이 되지 않습니다. R 3을 부하로 취급하여 Thevenin 정리나 Norton 정리를 사용할 수 있지만, 그게 무슨 재미가 있겠습니까?
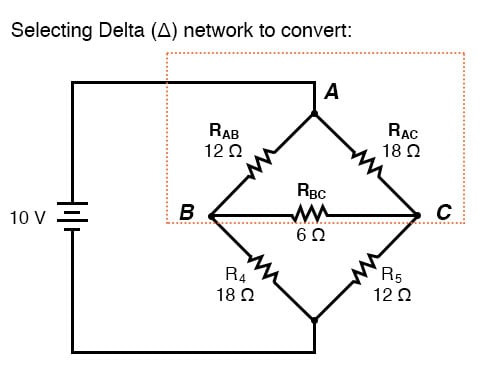
저항기 R 1 , R 2 , R 3 가 Δ 구성(각각 R ab , R ac , R bc )으로 연결되어 있다고 가정 하고 이를 대체하기 위한 동등한 Y 네트워크를 생성한다면 이 브리지 회로를 (더 간단한) 직렬/병렬 조합 회로 로 바꿀 수 있습니다 .
Δ-Y 변환 후...
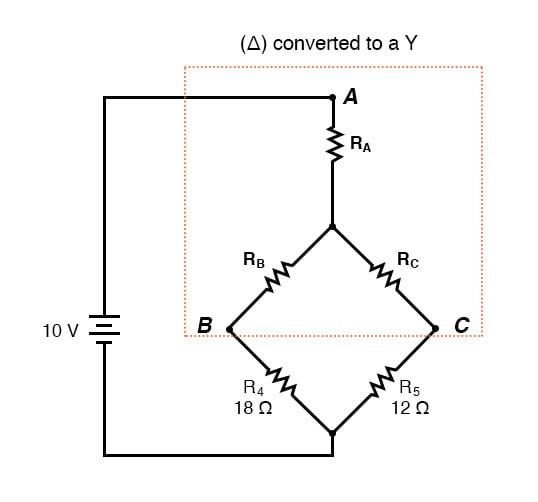
우리가 계산을 올바르게 수행한다면, 변환된 회로에서 A, B, C 지점 간의 전압은 원래 회로와 같을 것이고, 그 값을 원래 브리지 구성으로 다시 옮길 수 있습니다.
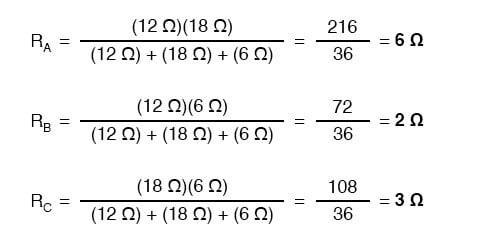
물론 저항기 R 4 와 R 5 는 각각 18 Ω와 12 Ω로 동일하게 유지됩니다. 이제 회로를 직렬/병렬 조합으로 분석하면 다음 그림에 도달합니다.
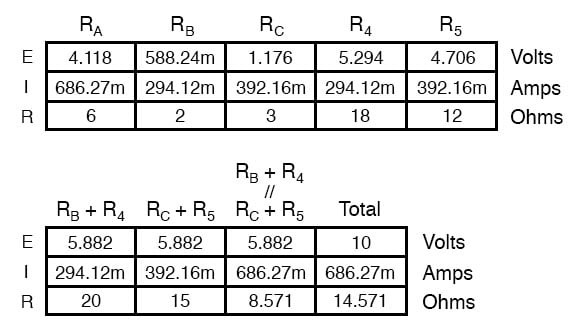
우리는 위 표의 전압 강하 수치를 사용하여 A, B, C 지점 사이의 전압을 결정하고 이들이 어떻게 합산되는지(또는 B와 C 지점 사이의 전압의 경우처럼 빼는지) 확인해야 합니다.
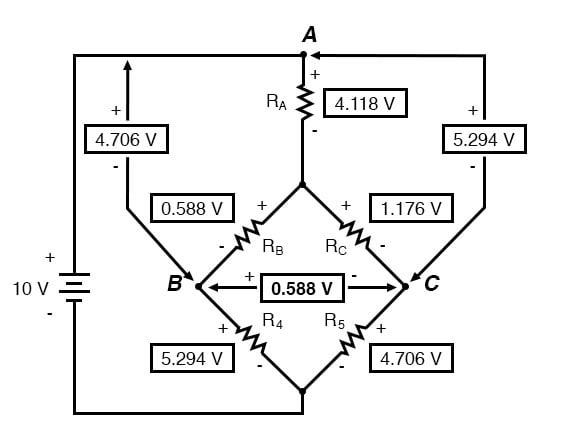

이제 우리는 이러한 전압을 알고 있으므로 이를 원래 브리지 회로의 동일한 지점 A, B, C로 전송할 수 있습니다.
물론, R 4 와 R 5 의 전압 강하는 컨버터 회로에서 발생하는 전압 강하와 정확히 동일합니다.
이 시점에서 우리는 이러한 전압을 취하고 옴의 법칙 (I=E/R)을 반복적으로 사용하여 저항 전류를 결정할 수 있습니다.

SPICE를 이용한 시뮬레이션
SPICE를 사용한 빠른 시뮬레이션은 우리의 작업을 검증하는 데 도움이 될 것입니다.

불평형 브리지 회로
v1 1 0
r1 1 2 12
r2 1 3 18
r3 2 3 6
r4 2 0 18
r5 3 0 12
.dc v1 10 10 1
.print dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0)
.끝
v1 v(1,2) v(1,3) v(2,3) v(2) v(3)
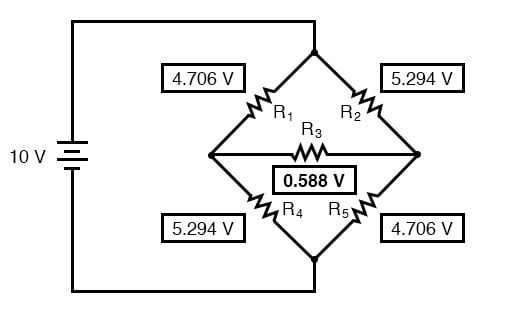
1.000E+01 4.706E+00 5.294E+00 5.882E-01 5.294E+00 4.706E+00
왼쪽에서 오른쪽으로 읽는 전압 수치는 R 1 ~ R 5 의 5개 저항에 걸리는 전압 강하를 나타냅니다 . 전류도 표시할 수 있었지만, 그렇게 하려면 SPICE 넷리스트에 "더미" 전압 소스를 삽입해야 했고, 우리는 주로 옴의 법칙이 아니라 Δ-Y 변환 방정식을 검증하는 데 관심이 있으므로 이것으로 충분합니다.
검토:
- "델타"(Δ) 네트워크는 "파이"(π) 네트워크라고도 합니다.
- "Y" 네트워크는 "T" 네트워크라고도 합니다.
- Δ 및 Y 네트워크는 적절한 저항 방정식을 사용하여 동등한 네트워크로 변환할 수 있습니다. "동등하다"는 말은 두 네트워크가 세 단자(A, B 및 C)에서 측정했을 때 전기적으로 동일하다는 것을 의미합니다.
- 브리지 회로는 절반을 Δ에서 Y 네트워크로 변환하여 직렬/병렬 회로로 단순화할 수 있습니다. 원래 세 연결 지점(A, B, C) 간의 전압 강하를 해결한 후, 해당 전압을 동일한 등가 지점을 통해 원래 브리지 회로로 다시 전송할 수 있습니다.