시간 경과에 따른 무효 DC 회로의 모든 값을 계산하는 확실한 방법이 있습니다.
반응성 DC 회로의 값 계산
첫 번째 단계는 커패시터나 인덕터가 변화에 반대하는 양에 대한 시작 값과 최종 값을 식별하는 것입니다. 즉, 반응성 구성 요소가 일정하게 유지하려고 하는 양입니다. 커패시터 의 경우 이 양은 전압 이고 인덕터 의 경우 이 양은 전류 입니다 . 회로의 스위치가 닫히거나 열리면 반응성 구성 요소는 스위치 전환 전과 동일한 수준으로 해당 양을 유지하려고 하므로 해당 값이 "시작" 값으로 사용됩니다.
이 양의 최종 값은 무한한 시간 후에 그 양이 될 것입니다. 이는 커패시터가 개방 회로인 것처럼 용량성 회로를 분석하고, 인덕터가 단락 회로인 것처럼 유도성 회로를 분석하여 결정할 수 있습니다. 왜냐하면 이러한 구성 요소가 무한한 시간 후에 "완전 충전"에 도달했을 때와 같이 동작하기 때문입니다.
다음 단계는 회로의 시간 상수를 계산하는 것입니다. 시간 상수는 과도 상황에서 전압 또는 전류 값이 시작 값에서 최종 값으로 약 63% 변경되는 데 걸리는 시간입니다.
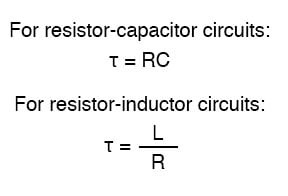
직렬 RC 회로 에서 시간 상수는 총 저항( 옴)에 총 커패시턴스(패럿)를 곱한 값과 같습니다. 직렬 L/R 회로 의 경우 총 인덕턴스(헨리)를 총 저항(옴)으로 나눈 값입니다. 어느 경우든 시간 상수는 초 단위로 표현 되며 그리스 문자 "타우"(τ)로 표시됩니다.
전압 및 전류와 같은 회로 값의 과도에 대한 반응으로의 상승 및 하락은 앞서 언급했듯이 점근적 입니다 . 따라서 값은 과도 직후에 빠르게 변하기 시작하여 시간이 지남에 따라 안정됩니다. 그래프에 표시하면 전압 및 전류의 최종 값에 대한 접근 방식은 지수 곡선을 형성합니다.
앞서 언급했듯이, 한 시간 상수는 이러한 값 중 하나가 시작 값에서 (궁극적인) 최종 값으로 약 63% 변경되는 데 걸리는 시간입니다. 시간 상수가 하나일 때마다 이러한 값은 최종 목표에 (대략) 63% 더 가까워집니다. 정확한 백분율을 결정하는 수학 공식은 매우 간단합니다.
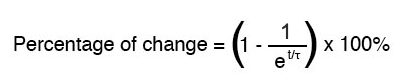
문자 e는 오일러 상수를 의미하며, 약 2.7182818입니다. 이는 회로 값의 점근적 접근 방식을 수학적으로 분석한 후 미적분 기법에서 파생되었습니다. 한 시간 상수의 시간 후, 시작 값에서 최종 값으로의 변화 백분율은 다음과 같습니다.
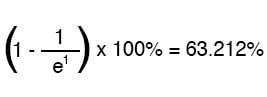
두 개의 시간 상수의 시간이 흐른 후, 시작 값에서 최종 값으로의 변화율은 다음과 같습니다.
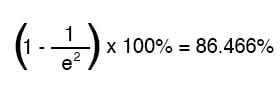
10개의 시간 상수의 시간이 흐른 후 백분율은 다음과 같습니다.
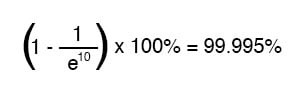
배터리에서 전압이 일시적으로 인가된 이후 시간이 지날수록 분수의 분모 값이 커지며, 이로 인해 전체 분수의 값은 작아지고, 총합(1에서 분수를 뺀 값)은 1 혹은 100%에 가까워집니다.
세계시상수 공식
과도 회로에서 전압과 전류 값을 결정하기 위한 이 공식을 최종 회로 값과 시작 회로 값의 차이로 곱하면 보다 보편적인 공식을 만들 수 있습니다.

이 장의 시작 부분에서 보여준 직렬 저항-커패시터 회로의 전압 상승을 분석해 보겠습니다.
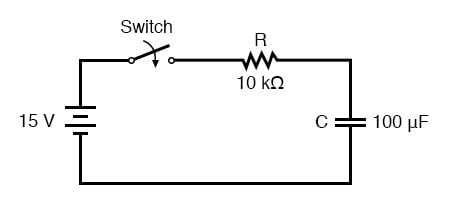
전압을 분석하기로 한 것은 전압이 커패시터가 일정하게 유지하는 경향이 있기 때문입니다. 이 공식은 전류에 대해 꽤 잘 작동하지만, 전류의 시작 및 최종 값은 실제로 커패시터의 전압에서 파생되므로 전압을 계산하는 것이 더 직접적인 방법입니다. 저항은 10kΩ이고 커패시턴스는 100µF(마이크로패럿)입니다. RC 회로의 시간 상수(τ)는 저항과 커패시턴스의 곱이므로 1초라는 값을 얻습니다.

커패시터가 완전히 방전된 상태(0볼트)에서 시작하면, 그 전압 값을 "시작" 값으로 사용할 수 있습니다. 물론 최종 값은 배터리 전압(15볼트)이 됩니다. 이 회로에서 커패시터 전압에 대한 우리의 보편적 공식은 다음과 같습니다.

따라서 닫힌 스위치를 통해 전압을 7.25초 동안 인가하면 커패시터 전압은 다음과 같이 증가합니다.
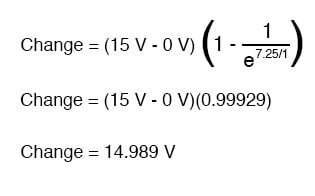
커패시터 전압을 0볼트에서 시작했으므로 14.989볼트가 증가하면 7.25초 후에는 14.989볼트가 됩니다.
같은 공식이 그 회로의 전류를 결정하는 데도 적용됩니다. 방전된 커패시터는 처음에는 단락 회로처럼 작동한다는 것을 알고 있으므로 시작 전류는 가능한 최대치인 15볼트(배터리에서)를 10kΩ(처음에 회로에서 전류에 대한 유일한 반대)로 나눈 값이 됩니다.

또한 최종 전류는 0이 될 것임을 알고 있습니다. 왜냐하면 커패시터는 결국 개방 회로로 작동하여 결국 전자가 회로에 흐르지 않을 것이기 때문입니다. 이제 시작 전류 값과 최종 전류 값을 모두 알았으므로 범용 공식을 사용하여 동일한 RC 회로에서 스위치가 닫힌 후 7.25초가 지난 후의 전류를 결정할 수 있습니다.

변화에 대해 얻은 수치는 양수가 아니라 음수라는 점에 유의하세요! 이는 시간이 지남에 따라 전류가 증가한 것이 아니라 감소했다는 것을 알려줍니다. 1.5mA의 전류에서 시작했기 때문에 이 감소(-1.4989mA)는 7.25초 후에 0.001065mA(1.065µA)가 있음을 의미합니다.
우리는 또한 커패시터 전압(14.989볼트)에서 배터리 전압(15볼트)을 빼서 10kΩ 저항기의 전압 강하를 구한 다음, 옴 의 법칙 (I=E/R)으로 저항기(및 전체 직렬 회로)를 통과하는 전류를 계산하여 시간=7.25초에서의 회로 전류를 결정할 수도 있었습니다. 어느 쪽이든 같은 답을 얻어야 합니다.

유도 회로 분석을 위한 범용 시간 상수 공식 사용
보편적 시간 상수 공식은 유도 회로를 분석하는 데도 잘 작동합니다. 이 장의 시작 부분에 있는 예제 L/R 회로에 적용해 보겠습니다.
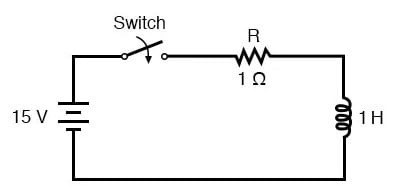
인덕턴스가 1 헨리이고 직렬 저항이 1 Ω일 때 시간 상수는 1초와 같습니다.

이것은 유도 회로이고, 우리는 인덕터가 전류의 변화에 반대한다는 것을 알고 있기 때문에, 우리는 전류의 시작 및 최종 값에 대한 시간 상수 공식을 설정할 것입니다. 스위치를 열린 위치에서 시작하면 전류는 0이 되므로 0이 우리의 시작 전류 값입니다.
스위치를 오랫동안 닫아 두면 전류는 최종 값으로 안정됩니다. 이 값은 전원 전압을 전체 회로 저항으로 나눈 값(I=E/R)과 같으며 이 회로의 경우 15암페어입니다.
3.5초에서의 전류 값을 결정하고자 하는 경우 다음과 같이 보편 시상수 공식을 적용합니다.
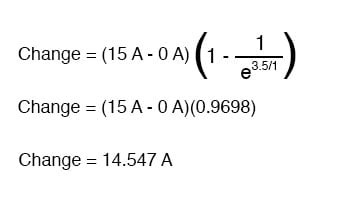
시작 전류가 0이었다는 사실을 고려하면 3.5초 후에 회로 전류는 14.547 암페어가 됩니다.
유도 회로의 전압을 결정하는 가장 좋은 방법은 먼저 회로 전류를 계산한 다음 저항을 통한 전압 강하를 계산하여 인덕터에 남은 전압 강하를 찾는 것입니다. 예제 회로에 저항이 하나뿐(1Ω 값)이므로 이는 매우 쉽습니다.

배터리 전압 15볼트에서 빼면 시간=3.5초에서 인덕터에 걸리는 전압은 0.453볼트입니다.

검토:
- 세계시상수 공식:
- RC 또는 L/R 회로를 분석하려면 다음 단계를 따르세요.
- (1): 회로(RC 또는 L/R)의 시간 상수를 결정합니다.
- (2): 계산할 양을 식별합니다(반응성 부품에 의해 직접적으로 변화가 방해되는 양. 커패시터의 경우 이는 전압이고 인덕터의 경우 이는 전류입니다).
- (3): 해당 수량에 대한 시작 값과 최종 값을 결정합니다.
- (4): 이러한 모든 값(최종, 시작, 시간, 시간 상수)을 범용 시간 상수 공식에 대입하여 수량 변화 를 구합니다.
- (5): 시작 값이 0이면 지정된 시간의 실제 값은 범용 공식에 의해 주어진 계산된 변화와 같습니다. 그렇지 않으면 시작 값에 변화를 추가하여 현재 위치를 파악합니다.