벡터를 그리지 않고 복소수 를 다루려면 먼저 어떤 종류의 표준 수학 표기법이 필요합니다. 복소수 표기법에는 극좌표 와 직교좌표 의 두 가지 기본 형태가 있습니다 .
복소수의 극형
극형은 복소수가 길이 ( 크기 , 절대값 또는 모듈러스 라고도 함 )와 벡터의 각도 (일반적으로 ∠와 같은 각도 기호로 표시)로 표시되는 방식입니다.
지도 비유를 사용하려면 뉴욕에서 샌디에이고까지의 벡터에 대한 극좌표 표기는 "2400마일, 남서쪽"과 같습니다. 벡터와 극좌표 표기의 두 가지 예는 다음과 같습니다.

극좌표 표기법을 사용한 벡터.
AC 회로 계산에서 벡터 각도에 대한 표준 방향은 0°를 오른쪽(수평)으로 정의하여 90° 수직 위로, 180° 왼쪽으로, 270° 수직 아래로 정의합니다. "아래로" 각도가 있는 벡터는 180을 초과하는 양수 또는 180 미만의 음수로 극좌표 형태로 표현된 각도를 가질 수 있습니다.
예를 들어, ∠ 270°(직선 아래) 각도를 가진 벡터는 -90° 각도를 갖는다고도 할 수 있습니다.(아래 그림) 오른쪽 위의 벡터(7.81 ∠ 230.19°)는 7.81 ∠ -129.81°로도 표시할 수 있습니다.
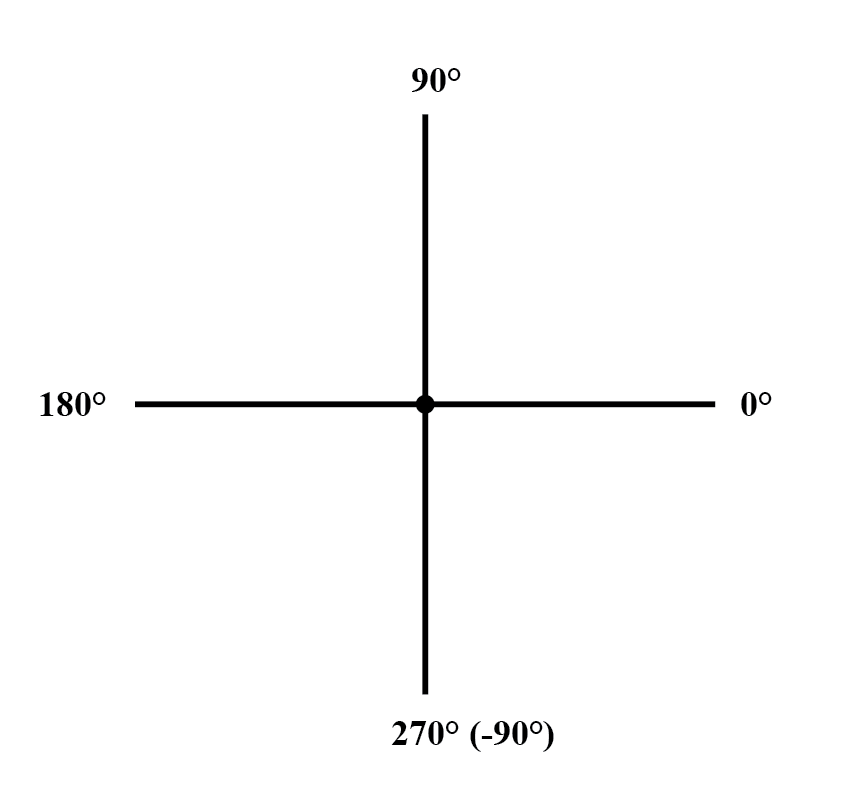
벡터 나침반.
복소수의 직사각형 형태
반면 직사각형 형태는 복소수가 각각의 수평 및 수직 구성 요소로 표시되는 경우입니다. 본질적으로 각진 벡터는 인접한 변과 반대편 변의 길이로 표현되는 직각 삼각형의 빗변으로 간주됩니다.
벡터의 길이와 방향을 크기와 각도로 표현하는 대신, "얼마나 왼쪽/오른쪽으로 떨어져 있는지"와 "얼마나 위/아래로 떨어져 있는지"로 표현합니다.
이러한 2차원 도형(수평 및 수직)은 두 개의 숫자로 표시됩니다. 수평 및 수직 차원을 서로 구별하기 위해 수직은 소문자 "i"(순수 수학의 경우) 또는 "j"(전자의 경우)로 접두사가 붙습니다.
이 소문자는 물리적 변수(즉시 전류, 소문자 "i"로 표시)를 나타내지 않지만, 벡터의 수직 성분과 수평 성분을 구별하는 데 사용되는 수학 연산자 입니다 . 완전한 복소수로서 수평 및 수직 양은 합으로 작성됩니다. (아래 그림)

"직사각형" 형태에서 벡터의 길이와 방향은 수평 및 수직 범위로 표시되며, 첫 번째 숫자는 수평("실수")을 나타내고 두 번째 숫자(접두사 "j" 포함)는 수직("허수") 차원을 나타냅니다.
수평 성분은 실수 성분 이라고 하는데 , 그 차원이 일반적인 스칼라("실수") 숫자와 호환되기 때문입니다. 수직 성분은 허수 성분 이라고 하는데, 그 차원이 실수의 규모와 전혀 다른 방향에 있기 때문입니다. (아래 그림)
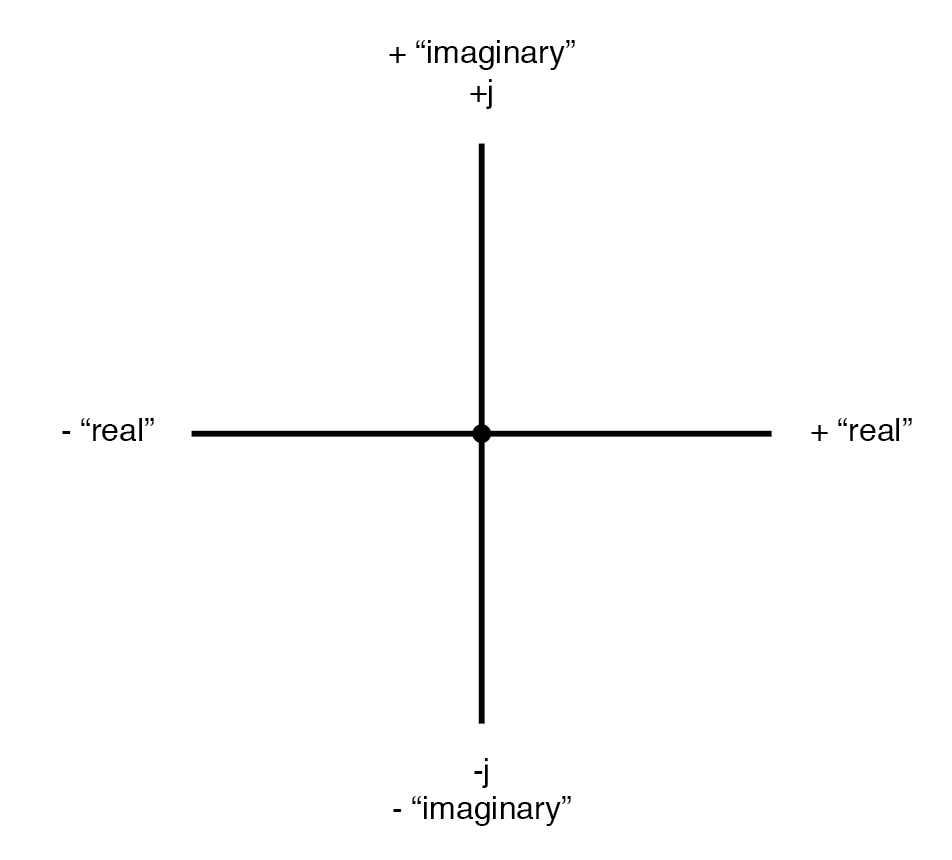
실수축과 허수축을 표시하는 벡터 나침반입니다.
그래프의 "실제" 축은 우리가 이전에 본 친숙한 숫자선에 해당합니다. 즉, 양수와 음수 값이 모두 있는 숫자선입니다. 그래프의 "가상" 축은 "실제" 축과 90° 각도로 위치한 또 다른 숫자선에 해당합니다.
벡터는 2차원적인 것이므로 벡터를 표현하기 위해 2차원 "맵"이 필요합니다. 따라서 서로 수직인 두 개의 숫자선이 필요합니다. (아래 그림)

실수와 허수("j") 숫자선이 있는 벡터 나침반.
극형에서 직사각형 형태로 변환
두 가지 표기법 모두 복소수에 유효합니다. 두 가지 표기법을 사용하는 주된 이유는 손으로 계산하기 쉽기 때문입니다. 직사각형 형태는 덧셈과 뺄셈에 적합하고, 극형 형태는 곱셈과 나눗셈에 적합합니다.
두 표기법 사이의 변환에는 간단한 삼각법이 필요합니다. 극좌표에서 직교좌표로 변환하려면 극좌표 크기에 각도의 코사인을 곱하여 실수 성분을 찾고, 극좌표 크기에 각도의 사인을 곱하여 허수 성분을 찾습니다.
이것은 양을 직각 삼각형의 변으로 그리면 더 쉽게 이해할 수 있습니다. 삼각형의 빗변은 벡터 자체(수평선에 대한 길이와 각도로 극형을 구성함)를 나타내고, 수평 및 수직 변은 각각 "실수" 및 "가상" 직사각형 구성 요소를 나타냅니다(아래 그림).

실수(4) 및 허수(j3) 성분에 따른 크기 벡터입니다.

직사각형 형태에서 극형 형태로 변환
직교 삼각형에서 극좌표로 변환하려면 피타고라스 정리를 사용하여 극좌표 크기를 구합니다 (극좌표 크기는 직각 삼각형의 빗변이고 실수 성분과 허수 성분은 각각 인접한 변과 대향 변입니다). 그리고 허수 성분의 아크탄젠트를 실수 성분으로 나누어 각도를 구합니다.

검토:
- 극좌표 표기법은 시작점으로부터 벡터의 길이와 각 방향으로 복소수를 나타냅니다. 예: 45마일 ∠ 203°(서쪽에서 남서쪽으로) 비행.
- 직사각형 표기법은 수평 및 수직 차원 측면에서 복소수를 나타냅니다. 예: 서쪽으로 41마일을 운전한 다음 방향을 돌려 남쪽으로 18마일을 운전합니다.
- 직사각형 표기법에서 첫 번째 양은 "실수" 성분(벡터의 수평 차원)이고 두 번째 양은 "허수" 성분(벡터의 수직 차원)입니다. 허수 성분 앞에는 소문자 "j"가 오는데, 이를 j 연산자 라고도 합니다 .
- 복소수의 극형 및 직사각형 표기법은 모두 직각 삼각형 형태로 그래픽적으로 연관시킬 수 있는데, 빗변은 벡터 자체를 나타내고(극형: 빗변의 길이 = 크기; 수평 변에 대한 각도 = 각도), 수평 변은 직사각형 "실수" 요소를 나타내고, 수직 변은 직사각형 "허수" 요소를 나타냅니다.