복소수는 스칼라 수와 마찬가지로 합법적인 수학적 개체이므로 다른 종류의 수와 마찬가지로 덧셈, 뺄셈, 곱셈, 나눗셈, 제곱, 반전 등의 연산이 가능합니다.
일부 과학 계산기는 두 개 이상의 복소수에 대해 이러한 연산을 직접 수행하도록 프로그래밍되어 있지만 이러한 연산은 "손으로" 수행할 수도 있습니다. 이 섹션에서는 기본 연산이 수행되는 방식을 보여드립니다.
복소수에서 산술 함수를 쉽게 수행할 수 있는 과학 계산기를 갖추는 것이 좋습니다 . 긴 방법으로 모든 계산을 해야 하는 경우보다 AC 회로에 대한 연구가 훨씬 더 즐거워질 것입니다.
직사각형 형태의 복소수의 덧셈과 뺄셈
직사각형 형태의 복소수에 대한 덧셈과 뺄셈은 쉽습니다. 덧셈의 경우, 복소수의 실수 성분을 더하여 합의 실수 성분을 결정하고, 복소수의 허수 성분을 더하여 합의 허수 성분을 결정합니다.

직사각형 형태의 복소수를 뺄 때, 두 번째 복소수의 실수 성분에서 첫 번째 복소수의 실수 성분을 빼면 차이의 실수 성분이 나오고, 두 번째 복소수의 허수 성분에서 첫 번째 복소수의 허수 성분을 빼면 차이의 허수 성분이 나옵니다.

극형 복소수의 곱셈과 나눗셈
손으로 곱셈과 나눗셈을 할 때는 극좌표가 선호되는 표기법입니다. 복소수를 극좌표 형태로 곱할 때는 복소수의 극좌표 크기를 곱하여 곱의 극좌표 크기를 결정하고 복소수의 각도를 더하여 곱의 각도를 결정합니다.
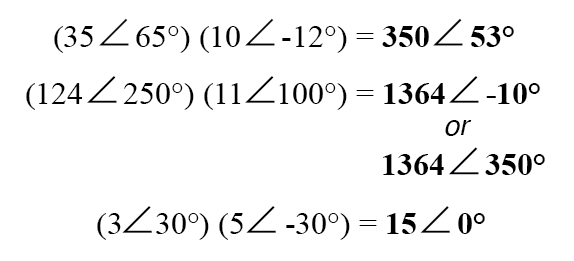
극형 복소수의 나눗셈도 쉽습니다. 첫 번째 복소수의 극형 크기를 두 번째 복소수의 극형 크기로 나누어 몫의 극형 크기를 구하고, 두 번째 복소수의 각도를 첫 번째 복소수의 각도에서 빼면 몫의 각도를 구할 수 있습니다.

복소수의 역수 또는 "반전"(1/x)을 구하려면 단순히 숫자(극형)를 스칼라 값 1로 나누면 됩니다. 이는 허수 성분이 없는(각도 = 0) 복소수에 불과합니다.

이것들은 AC 회로 분석에서 복소수를 조작하기 위해 알아야 할 기본 연산입니다. 그러나 복소수 연산은 단순히 덧셈, 뺄셈, 곱셈, 나눗셈, 역산에 국한되지 않습니다.
스칼라 수로 할 수 있는 거의 모든 산술 연산은 복소수에도 적용할 수 있습니다. 여기에는 거듭제곱, 제곱근, 복소수 계수를 갖는 연립 방정식 풀기, 심지어 삼각 함수도 포함됩니다(다만 이는 삼각법의 완전히 새로운 관점인 쌍곡선 함수 에 관한 것이므로 이 논의의 범위를 훌쩍 넘어섭니다).
덧셈, 뺄셈, 곱셈, 나눗셈, 역산과 같은 기본적인 산술 연산에 익숙해지면 AC 회로 분석 에 별 어려움이 없을 것입니다 .
검토:
- 복소수를 직사각형 형태로 더하려면 실수 성분을 더하고 허수 성분을 더합니다. 뺄셈도 비슷합니다.
- 복소수를 극형으로 곱하려면 크기를 곱하고 각도를 더합니다. 나누려면 크기를 나누고 한 각도에서 다른 각도를 뺍니다.