지난 섹션에서 우리는 저항 전용 및 커패시터 전용 AC 회로에서 어떤 일이 일어나는지 배웠습니다. 이제 두 구성 요소를 직렬 형태로 결합하고 효과를 조사합니다.

직렬 커패시터 회로: 전압은 전류보다 0°~90° 지연됩니다.
임피던스 계산
저항기는 주파수에 관계없이 AC 전류에 대해 5Ω의 저항을 제공하는 반면, 커패시터는 60Hz에서 AC 전류에 대해 26.5258Ω의 리액턴스를 제공합니다.
저항기의 저항은 실수(5 Ω ∠ 0° 또는 5 + j0 Ω)이고 커패시터의 리액턴스는 허수(26.5258 Ω ∠ -90° 또는 0 - j26.5258 Ω)이므로 두 구성 요소의 결합 효과는 두 숫자의 복소수 합의 값과 같은 전류에 대한 반대가 됩니다.
전류에 대한 이 복잡한 반대에 대한 용어는 임피던스 이고 , 기호는 Z이며, 저항 및 리액턴스와 마찬가지로 옴 단위로도 표현됩니다. 위의 예에서 총 회로 임피던스는 다음과 같습니다.

임피던스는 옴의 법칙 의 저항과 비슷한 방식으로 전압과 전류 와 관련됩니다 .

사실, 이것은 DC 전자학에서 가르친 것보다 훨씬 더 포괄적인 형태의 옴의 법칙입니다(E=IR). 임피던스가 전자 흐름에 대한 반대를 단순한 저항보다 훨씬 더 포괄적으로 표현하는 것과 마찬가지입니다. 모든 저항과 모든 리액턴스는 개별적으로 또는 조합(직렬/병렬)되어 단일 임피던스로 표현될 수 있으며 표현되어야 합니다.
현재 계산
위 회로에서 전류를 계산하려면 먼저 전압 소스에 대한 위상각 참조를 제공해야 하는데, 이는 일반적으로 0으로 가정됩니다. (저항성 및 용량성 임피던스의 위상각은 전압 또는 전류에 대한 주어진 위상각과 관계없이 각각 항상 0° 및 -90°입니다.)


순수한 용량성 회로와 마찬가지로 전류파가 전압파(소스)보다 앞서지만 이번에는 그 차이가 90°가 아닌 79.325°입니다.

직렬 RC 회로에서는 전압이 전류보다 지연됩니다(전류는 전압보다 앞서 있습니다).
테이블 방식
AC 인덕턴스 장에서 배웠듯이, 회로 양을 구성하는 "표" 방법은 DC 분석과 마찬가지로 AC 분석에도 매우 유용한 도구입니다. 이 직렬 회로에 대한 알려진 수치를 표에 넣고 이 도구를 사용하여 분석을 계속해 보겠습니다.

직렬 회로의 전류는 모든 구성 요소에 동일하게 공유되므로 전류에 대한 "전체" 열에 배치된 수치는 다른 모든 열에도 분배될 수 있습니다.
분석을 계속하면서 저항기와 커패시터의 전압을 결정하기 위해 옴의 법칙(E=IR)을 수직으로 적용할 수 있습니다.

저항기 양단의 전압이 전류와 정확히 같은 위상각을 가지고 있다는 점에 주목하세요. 이는 E와 I가 동상(저항기에만 해당)임을 알려줍니다. 커패시터 양단의 전압은 -10.675°의 위상각을 가지고 있으며, 회로 전류의 위상각보다 정확히 90° 작습니다 . 이는 커패시터의 전압과 전류가 여전히 서로 90° 위상이 틀렸다는 것을 알려줍니다.
SPICE를 사용한 계산
SPICE로 계산을 확인해 보겠습니다.
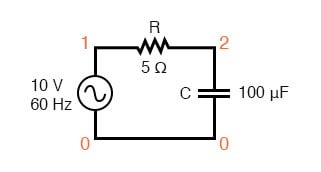
스파이스 회로: RC.
교류 rc 회로
v1 1 0 ac 10 sin
r1 1 2 5
씨1 2 0 100유
.ac 라인 1 60 60
.print ac v(1,2) v(2,0) i(v1)
.print ac vp(1,2) vp(2,0) ip(v1)
.끝
주파수 v(1,2) v(2) i(v1)
6.000E+01 1.852E+00 9.827E+00 3.705E-01
주파수 vp(1,2) vp(2) ip(v1)
6.000E+01 7.933E+01 -1.067E+01 -1.007E+02

SPICE는 다시 한번 혼란스럽게도 현재 위상각을 실수 위상각 더하기 180°(또는 빼기 180°)와 같은 값으로 인쇄합니다.
하지만 이 수치를 수정하고 우리의 작업이 올바른지 확인하는 것은 간단한 문제입니다. 이 경우, 현재 위상각에 대한 SPICE의 -100.7° 출력은 양의 79.3°와 같으며, 이는 이전에 계산한 수치인 79.325°와 일치합니다.
다시 한번 강조하지만, 실제 전압 및 전류 측정값에 해당하는 계산된 수치는 직사각형 형태가 아닌 극좌표 형태라는 점을 강조해야 합니다!
예를 들어, 실제로 이 직렬 저항기-커패시터 회로를 만들고 저항기 양단의 전압을 측정한다면, 전압계는 343.11 밀리볼트(실제 직사각형)나 1.8203볼트(가상 직사각형)가 아닌 1.8523볼트를 나타낼 것입니다.
실제 회로에 연결된 실제 계측기는 계산된 수치의 벡터 길이(크기)에 해당하는 표시를 제공합니다. 복소수 표기법의 직사각형 형태는 덧셈과 뺄셈을 수행하는 데 유용하지만, 극좌표보다 더 추상적인 표기법이며, 극좌표만 실제 측정과 직접 대응합니다.
직렬 RC 회로의 임피던스(Z)는 저항(R)과 용량성 리액턴스(X C )를 고려하여 계산할 수 있습니다. E=IR, E=IX C , E=IZ 이므로 저항, 리액턴스, 임피던스는 각각 전압에 비례합니다. 따라서 전압 위상 다이어그램을 유사한 임피던스 다이어그램으로 대체할 수 있습니다.
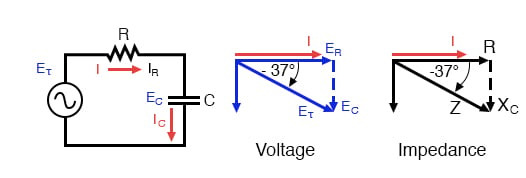
시리즈: RC 회로 임피던스 위상도.
예: 주어진 것: 88.42 마이크로패럿 커패시터와 직렬로 연결된 40Ω 저항기. 60Hz에서 임피던스를 찾으세요.
XC = 1/(2πfC)
XC = 1/(2π·60·88.42×10-6)
XC = 30Ω
Z = R - jXC
Z = 40 - j30
|Z| = sqrt(402 + (-30)2) = 50Ω
∠Z = 아크탄젠트(-30/40) = -36.87°
Z = 40 - j30 = 50∠-36.87°
검토:
- 임피던스는 전류에 대한 저항의 총 척도이며, (실수) 저항과 (가상) 리액턴스의 복소수(벡터) 합입니다.
- 임피던스(Z)는 직렬 회로 분석에서 저항(R)과 마찬가지로 관리됩니다. 직렬 임피던스는 합쳐져서 총 임피던스를 형성합니다. 모든 계산을 복소수(스칼라가 아님) 형태로 수행해야 합니다! Z Total1 + Z 2 + . . . Z n
- 임피던스는 임피던스를 구성하는 구성 요소의 유형에 관계없이 항상 직렬로 추가됩니다. 즉, 저항 임피던스, 유도 임피던스 및 용량 임피던스는 수학적으로 동일한 방식으로 처리해야 합니다.
- 순수 저항 임피던스는 항상 정확히 0°의 위상각을 갖습니다(Z R = R Ω ∠ 0°).
- 순수 용량성 임피던스는 항상 정확히 -90°의 위상각을 갖습니다(Z C = X C Ω ∠ -90°).
- 교류 회로에 대한 옴의 법칙: E = IZ ; I = E/Z ; Z = E/I
- 저항기와 커패시터가 회로에 섞여 있을 경우 전체 임피던스는 0°와 -90° 사이의 위상각을 갖게 됩니다.