무한 길이의 평행선
하지만 무한한 길이 의 평행선 세트가 있고 끝에 램프가 없다고 가정해 보자. 스위치를 닫으면 어떻게 될까? 전선 끝에 더 이상 부하가 없으므로 이 회로는 열려 있다. 전류가 전혀 없을까? (아래 그림)

무한한 전송선을 구동합니다.
이 "사고 실험"에서 초전도체를 사용하여 와이어 저항을 피할 수 있음에도 불구하고 와이어 길이를 따라 커패시턴스를 제거할 수는 없습니다. 절연 매체로 분리된 모든 도체 쌍은 해당 도체 사이에 커패시턴스를 생성합니다. (아래 그림)
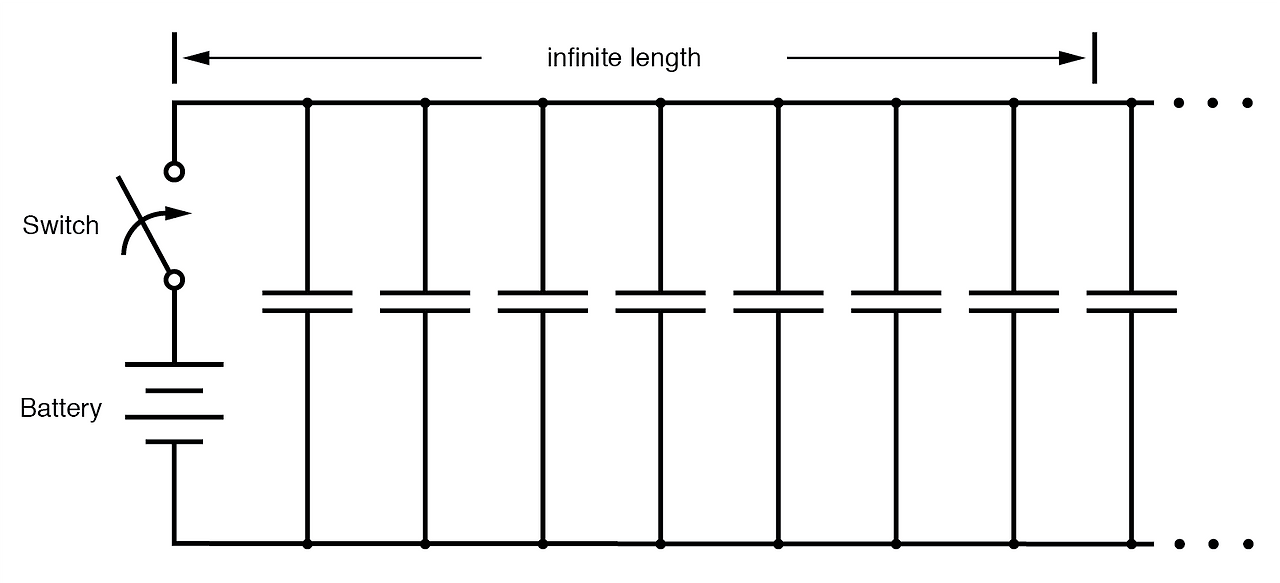
도체 사이의 부유 전기 용량을 보여주는 등가 회로.
두 도체 사이에 인가된 전압은 그 도체 사이에 전기장을 생성합니다 . 에너지는 이 전기장에 저장되고, 이 에너지 저장은 전압 변화에 대한 반대를 초래합니다. 전압 변화에 대한 커패시턴스의 반응은 i = C(de/dt) 방정식으로 설명되며, 이는 전류가 시간에 따른 전압의 변화율에 비례하여 인출된다는 것을 알려줍니다. 따라서 스위치가 닫히면 도체 사이의 커패시턴스는 충전되고 소스에서 전류를 인출하여 갑작스러운 전압 증가에 반응합니다. 방정식에 따르면, 완벽한 스위치 폐쇄로 인해 생성된 인가 전압의 순간적인 상승은 무한한 충전 전류를 발생시킵니다.
정전용량과 인덕턴스
그러나 평행한 한 쌍의 전선이 끌어낸 전류는 무한하지 않을 것입니다. 인덕턴스로 인해 전선을 따라 일련의 임피던스가 존재하기 때문입니다. (아래 그림) 모든 도체를 통과하는 전류는 비례 크기의 자기장을 발생 시킨다는 것을 기억하세요. 에너지는 이 자기장에 저장되고(아래 그림) 이 에너지 저장은 전류 변화에 대한 반대를 초래합니다. 각 전선은 전선 사이의 커패시턴스에 대한 충전 전류를 전달하면서 자기장을 발생시키고, 그렇게 하면서 인덕턴스 방정식 e = L(di/dt)에 따라 전압을 떨어뜨립니다. 이 전압 강하는 분산된 커패시턴스에서 전압 변화율을 제한하여 전류가 무한 크기에 도달하는 것을 방지합니다.

부유 용량과 인덕턴스를 보여주는 등가 회로.

전압은 정전용량을 전하시키고, 전류는 인덕턴스를 전하시킨다.
두 전선의 전하 캐리어가 거의 빛의 속도로 서로에게 움직임을 전달하고 서로에게서 전달하기 때문에 전압과 전류 변화의 "파면"은 같은 속도로 전선의 길이를 따라 전파되어 분포된 커패시턴스와 인덕턴스가 각각 다음과 같이 전체 전압과 전체 전류로 점진적으로 충전됩니다.

충전되지 않은 송전선.

파동 전파를 시작합니다.

파동의 전파를 계속합니다.

빛의 속도로 전파됩니다.
전송선
이러한 상호작용의 최종 결과는 배터리 소스를 통한 제한된 크기의 일정한 전류입니다. 전선이 무한히 길기 때문에 분포된 커패시턴스는 결코 소스 전압까지 완전히 충전되지 않으며 분포된 인덕턴스는 결코 무제한 충전 전류를 허용하지 않습니다. 다시 말해, 이 한 쌍의 전선은 스위치가 닫혀 있는 한 소스에서 전류를 끌어와 일정한 부하로 작동합니다. 더 이상 전선은 단순히 전류의 도체이자 전압의 캐리어가 아니라 고유한 특성을 가진 그 자체로 회로 구성 요소를 구성합니다. 더 이상 두 전선은 단순한 한 쌍의 도체가 아니라 전송선이 됩니다 .
일정한 부하로서, 전송선의 인가 전압에 대한 응답은 순수하게 인덕턴스와 커패시턴스로 구성되어 있음에도 불구하고(저항이 0인 초전도선이라고 가정) 반응성이 아니라 저항성입니다. 배터리 관점에서 볼 때 저항기가 에너지를 영원히 소산하는 것과 무한 전송선이 에너지를 영원히 흡수하는 것 사이에 차이가 없기 때문에 이렇게 말할 수 있습니다. 이 선의 임피던스(저항)를 옴으로 표시한 것을 특성 임피던스 라고 하며 , 두 도체의 기하 구조에 의해 고정됩니다. 공기 절연이 있는 평행선 선의 경우 특성 임피던스는 다음과 같이 계산할 수 있습니다.

전송선이 동축 구조로 구성된 경우 특성 임피던스는 다른 방정식을 따릅니다.

두 방정식 모두 분수의 두 항 모두에 동일한 측정 단위를 사용해야 합니다. 절연 재료가 공기(또는 진공)가 아닌 경우 특성 임피던스와 전파 속도가 모두 영향을 받습니다. 전송선의 실제 전파 속도와 진공에서의 빛의 속도의 비율을 해당 선의 속도 계수 라고 합니다.
속도 계수는 절연 재료의 상대 유전율( 유전 상수 라고도 함 )의 순전히 계수이며, 재료의 전기장 유전율과 순수 진공의 유전율의 비율로 정의됩니다. 동축이든 아니든 모든 케이블 유형의 속도 계수는 다음 공식으로 매우 간단하게 계산할 수 있습니다.

자연 임피던스
특성 임피던스는 자연 임피던스 라고도 하며 , 전압과 전류 "파동"이 빛의 속도의 상당 부분에 해당하는 전파 속도로 길이를 따라 전파될 때 분포된 커패시턴스와 인덕턴스로 인해 전송선이 무한히 길어졌을 때의 등가 저항을 말합니다.
첫 번째 두 방정식에서 전송선의 특성 임피던스(Z 0 )는 도체 간격이 증가함에 따라 증가한다는 것을 알 수 있습니다. 도체가 서로 멀어지면 분포 커패시턴스가 감소하고(커패시터 "플레이트" 사이의 간격이 커짐) 분포 인덕턴스가 증가합니다(두 개의 반대 자기장의 상쇄가 감소). 병렬 커패시턴스가 적고 직렬 인덕턴스가 클수록 주어진 양의 인가 전압에 대해 선이 끌어내는 전류가 작아지며, 이는 정의에 따라 더 큰 임피던스입니다. 반대로 두 도체를 더 가깝게 가져오면 병렬 커패시턴스가 증가하고 직렬 인덕턴스가 감소합니다. 두 가지 변화 모두 주어진 인가 전압에 대해 끌어내는 전류가 커져 임피던스가 낮아집니다.
유전체 "누설" 및 도체 저항과 같은 소산 효과가 없다면 전송선의 특성 임피던스는 단위 길이당 회선 인덕턴스를 단위 길이당 회선 커패시턴스로 나눈 비율의 제곱근과 같습니다.

검토:
- 전송선 은 길이를 따라 분포된 정전용량과 인덕턴스로 인해 특정한 특성을 나타내는 한 쌍의 병렬 도체입니다.
- 전송선의 한쪽 끝에 전압이 갑자기 인가되면 전압 '파동'과 전류 '파동'이 모두 거의 빛의 속도로 선을 따라 전파됩니다.
- 무한히 긴 전송선의 한쪽 끝에 직류 전압을 인가하면, 그 전송선은 마치 일정한 저항인 것처럼 직류 전원에서 전류를 끌어옵니다.
- 전송선의 특성 임피던스 (Z 0 )는 길이가 무한하다면 나타나는 저항입니다. 이는 두 도체를 분리하는 유전체의 누설 저항 및 전선 자체의 금속 저항과 완전히 다릅니다. 특성 임피던스는 순전히 선의 길이를 따라 분포된 커패시턴스와 인덕턴스의 함수이며 유전체가 완벽하고(무한 병렬 저항) 전선이 초전도성(직렬 저항이 0)이더라도 존재합니다.
- 속도 계수 는 진공에서 빛의 속도에 대한 전송선의 전파 속도와 관련된 분수 값입니다. 일반적인 2선 라인과 동축 케이블의 경우 값 범위는 0.66~0.80입니다. 모든 케이블 유형의 경우 케이블 절연의 상대 유전율 제곱근의 역수(1/x)와 같습니다.