
키르히호프의 전류 법칙
키르히호프 전류 법칙(KCL)은 교차점에 들어오고 나가는 전하 보존을 다루는 키르히호프의 첫 번째 법칙입니다.
전기 또는 전자 회로 주위에 흐르는 전류의 양이나 크기를 결정하려면 이러한 전류를 방정식의 형태로 기록할 수 있는 특정 법칙이나 규칙을 사용해야 합니다. 사용된 네트워크 방정식은 키르히호프의 법칙에 따른 방정식이며, 회로 전류를 다루면서 키르히호프의 전류 법칙(KCL)을 살펴보겠습니다.
구스타프 키르히호프(Gustav Kirchhoff)의 전류 법칙은 회로 분석에 사용되는 기본 법칙 중 하나입니다. 그의 전류법칙에 따르면 병렬 경로의 경우 회로 접합으로 들어가는 총 전류는 동일한 접합에서 나가는 총 전류와 정확히 동일합니다 . 요금이 손실되지 않아 더 이상 갈 곳이 없기 때문입니다.
즉, 접합점에 들어오고 나가는 모든 전류의 대수적 합은 다음과 같이 0과 같아야 합니다. Σ I IN = Σ I OUT .
Kirchhoff의 이 아이디어는 전류 손실 없이 접합부 주변에서 전류가 보존되기 때문에 일반적으로 전하 보존 으로 알려져 있습니다 . 단일 접합에 적용되는 키르히호프의 전류 법칙(KCL)의 간단한 예를 살펴보겠습니다.
단일 접합

이 간단한 단일 접합의 예에서 접합을 떠나는 전류 IT 는 동일한 접합으로 들어가는 두 전류 I 1 과 I 2 의 대수적 합입니다. 즉 I T = I 1 + I 2 입니다 .
이것을 I T – (I 1 + I 2 ) = 0 의 대수적 합으로 올바르게 작성할 수도 있습니다 .
따라서 I 1 이 3암페어이고 I 2가 2암페어인 경우 접합을 떠나는 총 전류 I T는 3 + 2 = 5 암페어가 되며 이 기본 법칙을 임의 개수의 접합 또는 노드에 대해 다음과 같이 사용할 수 있습니다. 들어오고 나가는 전류의 합은 동일합니다.
또한 전류의 방향을 바꾸더라도 결과 방정식은 I 1 또는 I 2 에 대해 여전히 유효합니다 . I 1 = I T – I 2 = 5 – 2 = 3암페어, I 2 = I T – I 1 = 5 – 3 = 2암페어. 따라서 접합으로 들어가는 전류는 양(+)으로, 접합에서 나가는 전류는 음(-)으로 생각할 수 있습니다.
그러면 우리는 접합점에 들어오거나 나가는 전류의 수학적 합이 어떤 방향으로든 항상 0과 같다는 것을 알 수 있으며, 이는 일반적으로 키르히호프 전류 법 (KCL) 으로 알려진 키르히호프 접합 법칙의 기초를 형성합니다. .
병렬 저항기
해당 분기의 저항이 같거나 같지 않은지 여부에 관계없이 병렬로 저항에 키르히호프의 전류 법칙을 적용할 수 있는 방법을 살펴보겠습니다. 다음 회로도를 고려하십시오.

이 간단한 병렬 저항기 예에는 전류에 대한 두 개의 서로 다른 접합이 있습니다. 접합점 1은 노드 B에서 발생하고 접합점 2는 노드 E에서 발생합니다. 따라서 우리는 이 두 개의 서로 다른 접합점 모두의 전류, 접합점으로 들어가는 전류 및 접합점을 떠나 흐르는 전류에 대해 키르히호프의 접합 규칙을 사용할 수 있습니다.
시작하려면 모든 전류 I T가 24V 공급 장치를 떠나 지점 A에 도달하고 거기에서 노드 B로 들어갑니다. 노드 B는 이제 전류가 두 개의 서로 다른 방향으로 분할될 수 있고 일부 전류가 아래로 흐를 수 있으므로 접합점입니다. 그리고 저항 R 1을 통해 나머지는 노드 C를 통해 저항 R 2 를 통해 계속됩니다 . 노드 지점으로 들어오고 나가는 전류를 일반적으로 분기 전류라고 합니다.
옴의 법칙을 사용하여 각 저항을 통과하는 개별 분기 전류를 다음과 같이 결정할 수 있습니다. I = V/R, 따라서:
저항 R 1 을 통해 전류 분기 B에서 E로의 경우

저항 R 2 를 통해 전류 분기 C에서 D로

위에서 우리는 키르히호프의 전류법칙에 따라 접합점으로 들어가는 전류의 합은 접합점을 떠나는 전류의 합과 같아야 하며 위의 간단한 예에서는 노드 B의 접합점으로 들어가는 하나의 전류 I T 가 있음을 알 수 있습니다. 그리고 접합점을 떠나는 두 개의 전류 I 1 과 I 2 .
이제 계산을 통해 노드 B의 접합점을 떠나는 전류가 I 1 은 3A이고 I 2 는 2A라는 것을 알았으므로 노드 B의 접합점으로 들어가는 전류의 합은 3 + 2 = 5A와 같아야 합니다. 따라서 Σ IN = I T = 5A입니다.
이 예에서는 노드 B와 노드 E에 두 개의 서로 다른 접합이 있으므로 두 전류가 노드 E에서 다시 재결합함에 따라 I T 에 대한 이 값을 확인할 수 있습니다 . 따라서 키르히호프의 접합 규칙이 참이 되도록 하려면 전류의 합은 F 지점으로의 전류는 노드 E의 접합부에서 흐르는 전류의 합과 같아야 합니다.
접점 E로 들어가는 두 전류는 각각 3암페어와 2암페어이므로 지점 F로 들어가는 전류의 합은 3 + 2 = 5암페어입니다. 따라서 Σ IN = I T = 5 암페어이므로 Kirchhoff의 전류 법칙은 현재 출발 지점 A와 동일한 값이므로 적용됩니다.
더 복잡한 회로에 KCL을 적용합니다.
키르히호프의 전류법칙을 사용하여 보다 복잡한 회로 주위에 흐르는 전류를 찾을 수 있습니다. 우리는 이제 노드(접합점)의 모든 전류의 대수적 합이 0과 같다는 것을 알고 있으며 이 아이디어를 염두에 두고 노드에 들어가는 전류와 노드에서 나가는 전류를 결정하는 간단한 경우입니다. 아래 회로를 고려하십시오.
키르히호프의 현행법 예 No1

이 예에는 노드 A, C, E 및 노드 F에서 전류가 분리되거나 병합되는 4개의 개별 접합이 있습니다. 공급 전류 I T 는 저항 R 1 및 R 2 를 통해 흐르는 노드 A에서 분리되고 이전 노드 C에서 재결합됩니다. 저항 R3, R4 및 R5를 통해 다시 분리되고 마지막 으로 노드 F 에서 다시 한 번 재결합됩니다.
그러나 각 저항 분기를 통해 흐르는 개별 전류를 계산하기 전에 먼저 회로의 총 전류 I T 를 계산해야 합니다 . 옴의 법칙에 따르면 I = V/R이며 V의 값인 132V를 알고 있으므로 다음과 같이 회로 저항을 계산해야 합니다.
회로 저항 R AC

따라서 노드 A와 C 사이의 등가 회로 저항은 1Ω으로 계산됩니다.
회로 저항 R CF

따라서 노드 C와 F 사이의 등가 회로 저항은 10Ω으로 계산됩니다. 그러면 총 회로 전류 IT는 다음 과 같이 주어진다.

다음과 같은 등가 회로를 제공합니다.
키르히호프의 전류법칙 등가회로
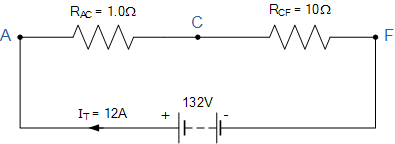
따라서 V = 132V, R AC = 1Ω, R CF = 10Ω, I T = 12A입니다.
등가 병렬 저항과 공급 전류를 설정한 후 이제 개별 분기 전류를 계산하고 다음과 같이 Kirchhoff의 접합 규칙을 사용하여 확인할 수 있습니다.

따라서 I 1 = 5A, I 2 = 7A, I 3 = 2A, I 4 = 6A, I 5 = 4A입니다.
접합점에 들어오고 나가는 전류를 계산하기 위해 노드 C를 기준점으로 사용하여 Kirchoff의 전류 법칙이 회로 주변에서 적용된다는 것을 확인할 수 있습니다.

또한 접합점으로 들어가는 전류는 양수이고 접합점을 떠나는 전류는 음수이므로 Kirchhoff의 전류 법칙이 참인지 다시 확인할 수 있습니다. 따라서 대수적 합은 다음과 같습니다. I 1 + I 2 – I 3 – I 4 – I 5 = 0은 5 + 7 – 2 – 6 – 4 = 0과 같습니다.
따라서 우리는 회로 네트워크의 접합점에서 전류의 대수적 합이 항상 0이라는 키르히호프의 전류 법칙(KCL)이 이 예에서 참이고 정확하다는 것을 분석을 통해 확인할 수 있습니다.
키르히호프의 현행법 예 No2
키르히호프의 전류법칙만을 이용하여 다음 회로 주위에 흐르는 전류를 찾아보세요.
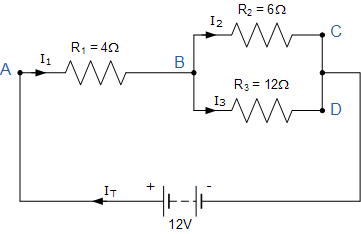
I T 는 12V 공급 전압에 의해 구동되는 회로 주위에 흐르는 총 전류입니다. 지점 A에서 I 1 은 IT 와 동일하므로 저항기 R 1 에 걸쳐 I 1 *R 전압 강하가 발생합니다 .
회로에는 2개의 분기, 3개의 노드(B, C 및 D) 및 2개의 독립 루프가 있으므로 두 루프 주변의 I*R 전압 강하는 다음과 같습니다.
- 루프 ABC ⇒ 12 = 4I 1 + 6I 2
- 루프 ABD ⇒ 12 = 4I 1 + 12I 3
키르히호프의 전류법칙에 따르면 노드 B에서 I 1 = I 2 + I 3 이므로 다음 루프 방정식 모두에서 전류 I 1을 (I 2 + I 3 )로 대체하고 단순화할 수 있습니다 .
키르히호프의 루프 방정식
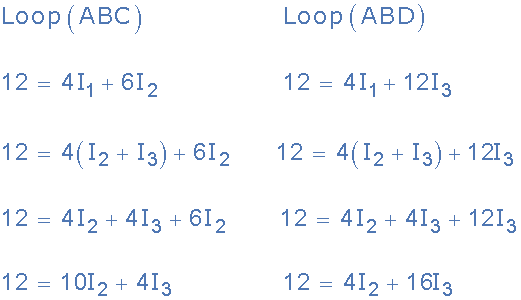
이제 회로 주위에 흐르는 전류와 관련된 두 가지 연립 방정식이 있습니다.
방정식. 아니오 1 : 12 = 10I 2 + 4I 3
방정식. 아니오 2 : 12 = 4I 2 + 16I 3
첫 번째 방정식(Loop ABC)에 4를 곱하고 Loop ABC에서 Loop ABD를 빼면 두 방정식을 모두 줄여 I 2 및 I 3 값을 얻을 수 있습니다.
방정식. 아니오 1: 12 = 10I 2 + 4I 3 ( x4 ) ⇒ 48 = 40I 2 + 16I 3
방정식. 아니오 2: 12 = 4I 2 + 16I 3 ( x1 ) ⇒ 12 = 4I 2 + 16I 3
방정식. 1번 – 방정식. 아니오 2 ⇒ 36 = 36I 2 + 0
I 2 를 I 3 으로 대체 하면 I 2 의 값이 1.0A가 됩니다 .
이제 첫 번째 방정식(Loop ABC)에 4를 곱하고 두 번째 방정식(Loop ABD)에 10을 곱하여 동일한 절차를 수행하여 I 3 의 값을 찾을 수 있습니다 . 다시 Loop ABD에서 Loop ABC를 빼면 두 방정식을 모두 줄일 수 있습니다. I 2 와 I 3 값을 제공하는 방정식
방정식. 아니오 1: 12 = 10I 2 + 4I 3 ( x4 ) ⇒ 48 = 40I 2 + 16I 3
방정식. 아니오 2: 12 = 4I 2 + 16I 3 ( x10 ) ⇒ 120 = 40I 2 + 160I 3
방정식. 아니오 2 – 방정식. 아니오 1 ⇒ 72 = 0 + 144I 3
따라서 I 2 를 I 3 으로 대체 하면 I 3 의 값이 0.5A가 됩니다 .
Kirchhoff의 접합 규칙에 따르면 I 1 = I 2 + I 3
저항 R1 을 통해 흐르는 공급 전류는 다음과 같이 주어진다: 1.0 + 0.5 = 1.5 Amps
따라서 I 1 = I T = 1.5 Amps , I 2 = 1.0 Amps 및 I 3 = 0.5 Amps 이며 해당 정보를 통해 장치 전체와 회로 주변의 다양한 지점(노드)에서 I*R 전압 강하를 계산할 수 있습니다.
예제 2의 회로는 옴의 법칙을 사용하여 간단하고 쉽게 풀 수 있었지만 여기서는 단순히 옴의 법칙을 적용할 수 없을 때 더 복잡한 회로를 풀 수 있는 방법을 보여주기 위해 키르히호프의 전류 법칙을 사용했습니다.