자기
전자기력은 전선이나 케이블과 같은 단순한 도체를 통해 전류가 흐를 때 생성되는 힘입니다.
자석은 주로 금속과 같은 다른 물질을 끌어당기거나 밀어내는 강자성 물질로 만들 수 있습니다. 자력은 자석이 서로 끌어당기거나 밀어낼 때 자석이 가하는 힘입니다. 도체를 통해 흐르는 전류의 방향에 따라 "북극" 및 "남극"에 대한 이 자기장의 방향이 결정되는 작은 자기장이 도체 주위에 생성됩니다.
자기가 없으면 릴레이 , 솔레노이드, 인덕터, 초크, 코일, 확성기, 모터, 발전기, 변압기 및 전기 계량기와 같은 구성 요소가 작동하지 않기 때문에 자기는 전기 전자 공학에서 중요한 역할을 합니다.
그러면 모든 와이어 코일은 전류가 흐를 때 전자기 효과를 사용합니다. 하지만 자성 , 특히 전자기학을 더 자세히 살펴보기 전에 물리학 수업에서 자석과 자성이 어떻게 작동하는지 기억해야 합니다.
자기의 본질
자석은 자성 광석의 형태로 자연 상태에서 발견될 수 있으며, 두 가지 주요 유형은 "산화철"이라고도 불리는 자철석 (FE 3 O 4 )과 "선도석"이라고도 불리는 Lodestone 입니다. 이 두 개의 천연 자석이 끈 조각에 매달려 있으면 항상 북쪽을 가리키는 지구 자기장과 일직선을 이루는 위치를 차지하게 됩니다.
이 효과의 좋은 예는 나침반 바늘입니다. 대부분의 실제 적용에서 이러한 자연 발생 자석은 자성이 매우 낮고 오늘날 인공 인공 자석이 다양한 모양, 크기 및 자기 강도로 생산될 수 있기 때문에 무시될 수 있습니다.
자력에는 기본적으로 "영구자석"과 "임시자석"의 두 가지 형태가 있으며, 용도에 따라 사용되는 유형이 다릅니다. 철, 니켈, 니켈 합금, 크롬 및 코발트와 같이 자석을 만드는 데 사용할 수 있는 다양한 유형의 재료가 있으며 자연 상태에서 니켈 및 코발트와 같은 일부 원소는 그 자체로 매우 낮은 자기량을 나타냅니다.
그러나 철이나 과산화알루미늄과 같은 다른 물질과 함께 혼합되거나 "합금"되면 "alcomax", "hycomax", "alni" 및 "alnico"와 같은 특이한 이름을 생성하는 매우 강한 자석이 됩니다.
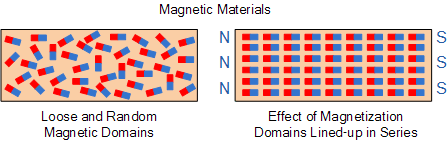
비자성 상태의 자성 물질은 느슨한 자기 사슬 형태 또는 무작위 패턴으로 느슨하게 배열된 개별 작은 자석 형태의 분자 구조를 갖습니다. 이러한 유형의 배열의 전반적인 효과는 각 분자 자석의 우연한 배열이 이웃을 중화시키는 경향이 있기 때문에 자성이 0이거나 매우 약한 결과를 낳습니다.
물질이 자화 되면 분자의 무작위 배열이 변경되고 작은 정렬되지 않은 무작위 분자 자석이 일련의 자기 배열을 생성하는 방식으로 "일렬로 정렬"됩니다. 강자성 물질의 분자 배열에 대한 이러한 아이디어는 웨버의 이론 으로 알려져 있으며 아래에 설명되어 있습니다.
철 조각과 자석의 자기 분자 배열

Weber의 이론은 원자 전자의 회전 작용으로 인해 모든 원자가 자기 특성을 갖는다는 사실에 기초합니다. 원자 그룹은 서로 결합하여 자기장이 모두 같은 방향으로 회전합니다. 자성 물질은 원자 주위의 분자 수준에서 작은 자석 그룹으로 구성되며, 자화된 물질은 대부분의 작은 자석이 한 방향으로만 정렬되어 한 방향으로는 북극을, 다른 방향으로는 남극을 생성합니다. .
마찬가지로 모든 방향을 가리키는 작은 분자 자석을 가진 물질은 이웃 자석에 의해 분자 자석이 중화되어 자기 효과가 중화됩니다. 이러한 분자 자석 영역을 "도메인"이라고 합니다.
모든 자성 물질은 궤도 및 회전 전자에 의해 설정된 물질의 자구 정렬 정도에 따라 자기장 자체를 생성합니다. 이 정렬 정도는 자화 M 으로 알려진 양으로 지정될 수 있습니다 .
자화되지 않은 재료에서는 M = 0 이지만 자기장이 제거되면 도메인 중 일부는 재료의 작은 영역에 정렬된 상태로 유지됩니다. 재료에 자화력을 가하는 효과는 일부 영역을 정렬하여 0이 아닌 자화 값을 생성하는 것입니다.
일단 자화력이 제거되면, 재료 내의 자성은 사용되는 자성 재료에 따라 빠르게 유지되거나 조용히 소멸됩니다. 자성을 유지하는 재료의 이러한 능력을 보유성( Retentivity) 이라고 합니다 .
자성을 유지해야 하는 재료는 유지력이 매우 높아 영구 자석을 만드는 데 사용되는 반면, 릴레이 및 솔레노이드 용 연철 코어와 같이 자성을 빨리 잃어야 하는 재료는 유지력이 매우 낮습니다.
자속
모든 자석은 모양에 관계없이 자기 회로 내부와 주변 모두에서 자기 주위에 보이지 않는 선속 선의 조직적이고 균형 잡힌 패턴의 명확한 체인을 생성하는 자기력을 갖는 자극이라고 불리는 두 개의 영역을 가지고 있습니다. 이러한 자속선을 집합적으로 자석의 "자기장"이라고 합니다. 이 자기장의 모양은 일부 부분에서 다른 부분보다 더 강하며, 가장 큰 자성을 갖는 자석 영역을 "극"이라고 합니다. 자석의 양쪽 끝에는 극이 있습니다.
이러한 플럭스 선(벡터장이라고 함)은 육안으로는 볼 수 없지만 종이 위에 철제 충전물을 뿌리거나 작은 나침반을 사용하여 추적하면 시각적으로 볼 수 있습니다. 자극은 항상 쌍으로 존재하며, 항상 북극 이라고 불리는 자석 영역이 있고 항상 남극 이라고 불리는 반대 영역이 있습니다 .
자기장은 항상 자속선이 더 조밀하고 집중된 물질의 각 끝 부분에 명확한 극을 제공하는 힘의 선으로 시각적으로 표시됩니다. 방향과 강도를 나타내는 자기장을 구성하는 선은 힘의 선 또는 보다 일반적으로 "자속" 이라고 하며 아래와 같이 그리스 기호 파이 ( Φ )로 표시됩니다.
막대자석 자기장의 힘선
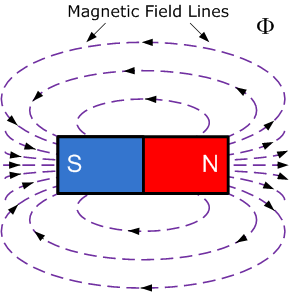
위에 표시된 것처럼 자기장은 자속선의 간격이 더 가까울수록 자석의 극 근처에서 가장 강합니다. 자속 흐름의 일반적인 방향은 북극 ( N ) 에서 남 ( S )극으로 향합니다. 또한, 이러한 자기선은 자석의 북극에서 출발하여 남극으로 들어가는 폐쇄 루프를 형성합니다. 자극은 항상 쌍으로 되어 있습니다.
그러나 자속은 자기력이 존재하는 자석 주변의 정적 영역이므로 실제로 자속은 북극에서 남극으로 흐르거나 아무데나 흐르지 않습니다. 즉, 자속은 흐르거나 움직이지 않고 단지 그 자리에 있으며 중력의 영향을 받지 않습니다. 힘의 선을 그릴 때 몇 가지 중요한 사실이 드러납니다.
- 힘의 선은 절대 교차하지 않습니다.
- 힘의 선은 연속적 입니다 .
- 자력선은 항상 자석 주위에 개별 폐쇄 루프를 형성합니다.
- 병력선은 북쪽에서 남쪽으로 명확한 방향을 가지고 있습니다.
- 서로 가까이 있는 자력선은 강한 자기장을 나타냅니다.
- 더 멀리 떨어져 있는 자력선은 약한 자기장이 있음을 나타냅니다.
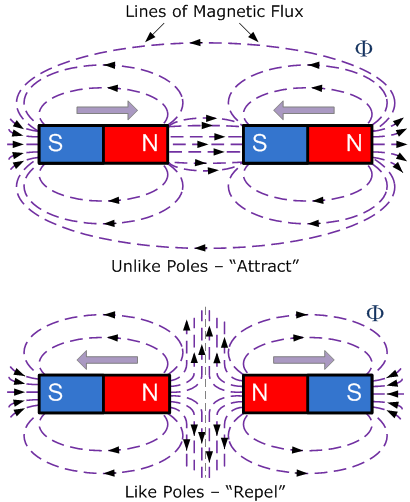
자기력은 전기력처럼 끌어당기고 밀어냅니다. 두 개의 힘선이 서로 가까워지면 두 자기장 사이의 상호 작용으로 인해 다음 두 가지 중 하나가 발생합니다.
- 1. – 인접한 극이 동일할 때(북-북 또는 남-남) 서로 밀어냅니다 .
- 2. – 인접한 극이 동일하지 않은 경우(북-남 또는 남-북) 서로 끌어당깁니다 .
이 효과는 "반대 부분이 서로 끌어당긴다"는 유명한 표현으로 쉽게 기억되며, 이러한 자기장의 상호 작용은 자석 주위에 자력선을 표시하기 위해 철 충전재를 사용하여 쉽게 설명할 수 있습니다. 유사한 극은 밀어내고 다른 극은 끌어당기는 등 다양한 극 조합이 자기장에 미치는 영향을 아래에서 볼 수 있습니다.
같은 극과 다른 극의 자기장
나침반을 사용하여 자기장선을 그릴 때 자력선이 북극을 떠나 자석의 각 끝에서 명확한 극을 제공하는 방식으로 자력선이 생성되어 북극으로 다시 들어가는 것을 볼 수 있습니다. 남극. 자성은 자성체를 가열하거나 망치로 두드려서 파괴할 수 있지만 단순히 자석을 두 조각으로 부수는 것만으로는 파괴되거나 분리될 수 없습니다.
따라서 일반 막대 자석을 두 조각으로 쪼개면 자석의 두 부분이 있는 것이 아니라 깨진 각 조각마다 고유한 북극과 남극이 있게 됩니다. 그 조각 중 하나를 가져다가 다시 두 개로 나누면 각각의 작은 조각에는 북극과 남극 등이 있게 됩니다. 자석 조각이 아무리 작아도 각 조각에는 여전히 북극과 남극이 있을 것입니다.
그런 다음 전기 또는 전자 계산에서 자기를 활용하려면 자기의 다양한 측면이 무엇인지 정의해야 합니다.
자기력의 크기
이제 우리는 자성 물질 주위의 자력선 또는 더 일반적으로 자속이 그리스 기호 Phi ( Φ )로 표시되고 플럭스 단위는 Wilhelm Eduard Weber의 이름을 따서 Weber ( Wb )라는 것을 알고 있습니다. 그러나 주어진 단위 면적 내의 힘선의 수를 "자속 밀도"라고 하며 자속( Φ )은 ( Wb ) 단위 로 측정되고 면적( A )은 제곱미터( m 2 ) 단위로 측정되므로 자속 밀도가 측정됩니다. Webers /Metre 2 또는 ( Wb/m 2 )이며 기호 B 로 표시됩니다 .
그러나 자기학에서 자속밀도를 언급할 때 자속밀도는 니콜라 테슬라 다음에 테슬라 의 단위를 부여하므로 1Wb/m 2 는 1 테슬라와 같으므로 1Wb/m 2 = 1T 입니다 . 자속 밀도는 힘의 선에 비례하고 면적에 반비례하므로 자속 밀도를 다음과 같이 정의할 수 있습니다.
자속밀도
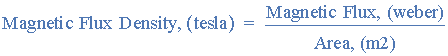
자속밀도의 기호는 B 이고 자속밀도의 단위는 Tesla, T 이다 .
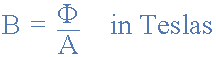
자속 밀도에 대한 모든 계산은 동일한 단위(예: 웨버의 자속, m2의 면적, 테슬라의 자속 밀도)로 수행된다는 점을 기억하는 것이 중요합니다.
자기 예제 No1
둥근 자기 막대에 존재하는 자속의 양은 0.013 웨버로 측정되었습니다. 재료의 직경이 12cm인 경우 자속 밀도를 계산하십시오.
자성체의 단면적(m2)은 다음과 같습니다.
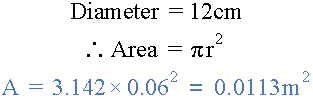
자속은 0.013 웨버로 주어지므로 자속 밀도는 다음과 같이 계산할 수 있습니다.
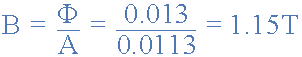
따라서 자속 밀도는 1.15 Tesla로 계산됩니다.
전기 회로의 자성을 다룰 때 1테슬라는 자기장에 직각으로 1암페어를 전달하는 도체가 1뉴턴 미터 길이의 힘을 받는 자기장의 밀도라는 것을 기억해야 합니다. 전자기학에 대한 다음 튜토리얼에서 설명하겠습니다.
'전자일기' 카테고리의 다른 글
| 전자석 (0) | 2024.02.05 |
|---|---|
| 전자기학 (0) | 2024.02.05 |
| 쇼트키 다이오드 (1) | 2024.02.05 |
| 다이오드 클리핑 회로 (0) | 2024.02.05 |
| 태양광 패널의 바이패스 다이오드 (0) | 2024.02.05 |