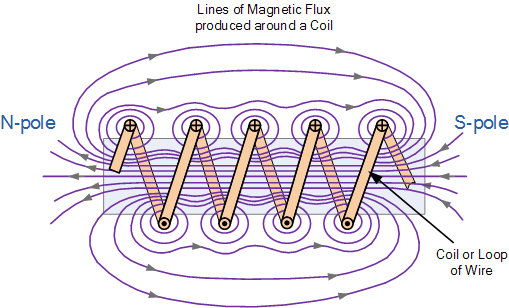
전자석
큰 못과 같은 연철 코어 주위에 와이어 코일을 감으면 간단한 전자석을 만들 수 있습니다.
전자석은 전류에 의해 자기장이 생성되는 임시자석의 일종으로, 자기장을 집중시키기 위해 전자석의 선을 코일로 감은 형태이다.
이제 우리는 이전 튜토리얼을 통해 직선 전류가 흐르는 도체가 길이를 따라 모든 지점에서 자신 주위에 원형 자기장을 생성하고 이 자기장의 회전 방향이 도체를 통과하는 전류 흐름 방향(왼손)에 따라 달라진다는 것을 알고 있습니다 . 규칙 .
전자기학에 대한 마지막 튜토리얼에서 우리는 도체를 단일 루프로 구부리면 전류가 시계 방향 필드와 시계 반대 방향 필드를 생성하는 루프를 통해 반대 방향으로 흐르게 된다는 것을 보았습니다. 전자석 은 여러 개의 개별 루프를 자기적으로 결합하여 단일 코일을 생성함으로써 이 원리를 사용합니다.
전자석은 기본적으로 전류가 코일을 통과할 때 뚜렷한 북극과 남극이 있는 막대 자석처럼 동작하는 와이어 코일입니다. 각 개별 코일 루프에 의해 생성된 정적 자기장은 코일 중심의 마지막 튜토리얼에서 살펴본 단일 와이어 루프처럼 집중된 결합 자기장을 사용하여 이웃 코일과 합산됩니다. 한쪽 끝에 N극이 있고 다른 쪽 끝에 S극이 있는 결과적인 정자장은 균일하며 외부 주변보다 코일 중앙에서 훨씬 더 강합니다.
전자석 주위의 힘선
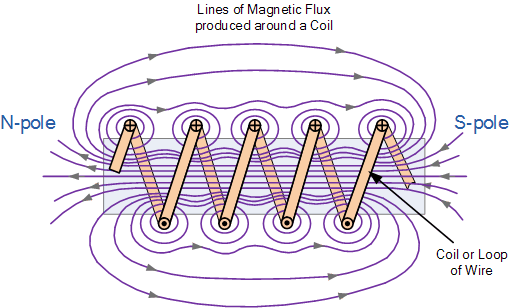
이것이 생성하는 자기장은 막대 자석 형태로 뻗어 있어 코일에 흐르는 전류의 양에 비례하는 플럭스와 함께 독특한 북극과 남극을 제공합니다. 동일한 전류가 흐르는 동일한 코일에 추가 와이어 층을 감으면 자기장의 강도가 증가합니다.
따라서 주어진 자기 회로에서 사용할 수 있는 자속의 양은 이를 통해 흐르는 전류와 코일 내 와이어의 회전 수에 정비례한다는 것을 알 수 있습니다. 이 관계를 Magneto Motive Force ( mmf) 라고 하며 다음과 같이 정의됩니다.

자기 원동력은 N 턴 의 코일을 통해 흐르는 전류 I 로 표현됩니다 . 따라서 전자석의 자기장 세기는 코일의 암페어 회전수 에 의해 결정되며 , 코일에 도선을 많이 감으면 자기장의 세기도 커집니다.
전자석의 자기 강도
이제 우리는 인접한 두 도체에 전류가 흐르고 전류 흐름 방향에 따라 자기장이 형성된다는 것을 알고 있습니다. 결과적으로 두 필드의 상호 작용으로 인해 두 도체가 기계적 힘을 경험하게 됩니다.
전류가 같은 방향(코일의 같은 쪽)으로 흐르면 두 도체 사이의 자기장이 약해 위와 같이 인력이 발생합니다. 마찬가지로, 전류가 반대 방향으로 흐르면 이들 사이의 자기장이 강화되고 도체는 반발됩니다.
도체 주변의 이 필드의 강도는 도체 옆에 가장 강한 지점이 있고 도체에서 멀어질수록 점차 약해지는 점과 거리에 비례합니다. 단일 직선 도체의 경우 흐르는 전류와 그로부터의 거리가 필드의 강도를 결정하는 요소입니다.
따라서 긴 직선 전류가 흐르는 도체의 "자기장 강도", H를 "자기력"이라고도 하는 계산 공식은 도체를 통해 흐르는 전류와 도체로부터의 거리에서 파생됩니다.
전자석의 자기장 강도

- 어디:
- H – 자기장의 강도(암페어 턴/미터, At/m) 입니다.
- N - 코일의 회전 수입니다.
- 나는 – 코일을 통해 흐르는 전류(암페어, A) 입니다.
- L – 코일의 길이(미터), m
요약하자면, 코일 자기장의 강도는 다음 요소에 따라 달라집니다.
- 코일 내 와이어의 회전 수입니다.
- 코일에 흐르는 전류의 양.
- 핵심 재료의 유형.
전자석의 자기장 강도는 코어의 주요 목적이 잘 정의되고 예측 가능한 경로에 자속을 집중시키는 것이므로 사용되는 코어 재료의 유형에 따라 달라집니다. 지금까지는 공기 코어(중공) 코일만 고려되었지만 코어(코일의 중심)에 다른 재료를 도입하면 자기장의 강도에 매우 큰 제어 효과가 있습니다.
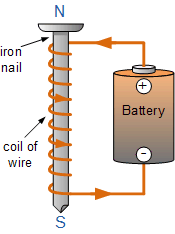
못을 이용한 전자석
예를 들어 목재와 같이 재료가 비자성인 경우 투자율 값이 매우 낮으므로 계산 목적으로 자유 공간으로 간주할 수 있습니다. 그러나 코어 재료가 철, 니켈, 코발트 또는 이들 합금의 혼합물과 같은 강자성 재료로 만들어진 경우 코일 주변의 자속 밀도에 상당한 차이가 관찰됩니다.
강자성 물질은 자화될 수 있고 일반적으로 연철, 강철 또는 다양한 니켈 합금으로 만들어집니다. 이러한 유형의 재료를 자기 회로에 도입하면 자속을 집중시켜 밀도를 높이고 코일의 전류에 의해 생성된 자기장을 증폭시키는 효과가 있습니다.
그림과 같이 큰 연철 못 주위에 와이어 코일을 감고 이를 배터리에 연결하여 이를 증명할 수 있습니다. 이 간단한 교실 실험을 통해 우리는 많은 양의 클립이나 핀을 집어들 수 있고 코일에 더 많은 회전을 추가하여 전자석을 더 강하게 만들 수 있습니다. 속이 빈 공기 코어 또는 코어에 강자성 물질을 도입함으로써 발생하는 자기장의 강도 정도를 자기 투자율(Magnetic Permeability) 이라고 합니다 .
전자석의 투자율
물리적 크기가 동일한 서로 다른 재료의 코어가 전자석에 사용되는 경우 자석의 강도는 사용되는 코어 재료에 따라 달라집니다. 자기 강도의 이러한 변화는 중앙 코어를 통과하는 자속선의 수로 인해 발생합니다. 자성 재료의 투자율이 높으면 자속선이 쉽게 생성되어 중앙 코어를 통과할 수 있으며 투자율(μ)은 코어가 자화될 수 있는 용이성을 나타내는 척도입니다.
진공의 투자율에 대해 주어진 수치 상수는 다음과 같이 제공됩니다. μ o = 4.π.10 -7 H/m 자유 공간(진공)의 상대 투자율은 일반적으로 1의 값으로 제공됩니다. 투과성을 다루는 모든 계산에서 기준으로 사용되는 것은 이 값이며, 모든 재료에는 고유한 투과성 값이 있습니다.
다양한 철, 강철 또는 합금 코어의 투자율만 사용하는 경우의 문제점은 관련된 계산이 매우 커질 수 있으므로 상대 투자율로 재료를 정의하는 것이 더 편리하다는 것입니다.
상대 투자율 , 기호 μr 은 μ (절대 투자율 )와 μo 자유 공간 투자율의 곱으로 다음과 같이 표현됩니다 .
상대 투자율

물, 구리, 은, 금과 같이 투자율이 자유 공간(진공)보다 약간 낮고 자기장에 대해 약한 음의 민감성을 갖는 물질을 반자성이라고 합니다 . 가스, 마그네슘, 탄탈륨과 같이 투자율이 자유 공간보다 약간 크고 자기장에 의해 약간만 끌어당기는 물질을 상자성이라고 합니다 .
전자석 예 No1
연철 코어의 절대 투자율은 80밀리헨리/m(80.10 -3 )로 제공됩니다. 등가 상대 투자율 값을 계산합니다.

강자성 물질이 코어에 사용되는 경우 상대 투자율을 사용하여 자기장 강도를 정의하면 사용되는 다양한 유형의 재료에 대한 자기장의 강도에 대한 더 나은 아이디어를 얻을 수 있습니다. 예를 들어, 진공과 공기의 상대 투자율은 1이고 철심의 경우 약 500입니다. 따라서 철심의 전계 강도는 동등한 중공 공기 코일보다 500배 더 강하다고 말할 수 있으며 이 관계는 훨씬 더 큽니다. 0.628×10 -3 H/m, ( 500.4.π.10 -7 ) 보다 이해하기 쉽습니다 .