
파형의 파고율
파고율은 순수 사인파의 파고율이 1.414인 경우 피크 값과 RMS 값의 비율로 파형의 모양을 설명합니다.
파고율 ( C F )은 다양한 유형의 주기적인 파형을 분석하는 데 사용할 수 있는 또 다른 수학적 관계입니다. 피크 인자(Peak Factor ) 또는 진폭 인자(Amplitude Factor) 라고도 하는 파고율(Crest Factor) 은 주기적인 파형이 다양한 모양을 가질 수 있으므로 특정 주기적인 파형의 품질을 정의하는 데 사용됩니다.
파형 피크 인자는 AC 회로에 적용되는 최대 전압을 나타낼 수 있으므로 매우 중요합니다. 예를 들어, 커패시터나 전기 케이블의 절연 파괴 전압은 사용되는 교류 전압의 최대 전압에 따라 달라집니다. 따라서 모든 AC 구성 요소는 적용된 전압의 RMS 값이 아닌 파고 전압을 견딜 수 있어야 합니다.
전기전자 공학에서 사용하는 가장 일반적인 주기 파형은 사인파형 입니다 . 전압 또는 전류의 교류 사인파는 표시된 대로 최대값 , 평균값 및 RMS( 근평균 제곱근 ) 값으로 정의할 수 있습니다.
정현파형

모든 파형의 최대 진폭, A max는 일반적으로 피크 또는 최대 값 이라고 합니다 . 모든 정현파의 경우 최대 양수 값 또는 양수 피크 값은 축을 따라 90 ° 의 회전 각도에서 도달됩니다. 최대 음수 값 또는 음수 피크 값은 전체 사이클 1회에 걸쳐 270° 각도 에서 도달됩니다 . 따라서 순수 사인파에는 두 개의 동일하지만 반대되는 최대 피크 값, 즉 양의 피크인 +A max 와 음의 피크인 -A max가 있습니다 .
교번 파형은 시간에 따라 주기적으로 변하므로 일정하거나 안정된 상태 값을 갖지 않습니다. 저항기에서 동일한 I 2 R 가열 효과를 생성하는 등가 DC 값은 Root-Mean-Square 또는 RMS 값으로 알려져 있습니다.
교류파의 RMS 값은 하나 의 전체 사이클에 걸쳐 계산된 파동의 유효 값이며 다음과 같이 제공됩니다.
A rms = A 최대 / √ 2 = (1/√ 2 )A 최대 = 0.7071×A 최대
그러면 최대 피크 값 과 파고율 로 표현될 수 있는 교번 파형의 rms 값 사이에 직접적인 관계가 있음을 알 수 있습니다 . 따라서 모든 파형의 파고율은 다음과 같이 정의됩니다.
기본 파고율 공식

따라서 순수 사인파의 파고율은 다음과 같이 정의됩니다.

따라서 파고율은 주기적인 파형의 피크 값을 rms 값으로 나눈 비율로 정의된다는 것을 알 수 있습니다. 따라서 구형파를 포함한 모든 교류 신호의 경우 파고율 값은 항상 1(단위)보다 크고 정점이 높아질수록 파고율도 증가합니다.
사인파가 완전 정현파인 경우 파고율은 피크 값에 관계없이 항상 1.414 , (√ 2 )와 같습니다.
파고율 예 No1
정현파의 최대 피크 값은 232V입니다. 파고율을 계산합니다.

예상대로 사인파형 입니다 .
파고율 예 No2
교류 전압의 최대 피크 값은 96V이고 파고율은 1.5입니다. rms 값을 계산합니다.

위의 설명에서는 파형이 순전히 정현파라고 가정하지만, 주파수, 주기 및 피크 값은 모두 동일한 의미를 가지므로 구형파와 같은 기타 비정현파 반복 파형에 대해 파고율을 계산할 수 있습니다.
이는 기본 주파수를 기준으로 서로 다른 홀수 고조파 주파수에서 합산된 무한한 수의 사인파로부터 구형파를 생성할 수도 있기 때문입니다.
구형파 파고율
사각형 모양의 주기파는 접지를 중심으로 두 개의 고정 값이 순간적으로 번갈아 나타나는 또 다른 유형의 주기파로 분류될 수 있습니다. 시간의 최대값 지속 시간은 최소값의 지속 시간과 같습니다. 그러면 구형파는 듀티 사이클이 50%이고 기간이 동일한 특수한 형태의 직사각형 파형이므로 파고율 값을 계속 찾을 수 있습니다.
사각파(양극) 파형

주기적인 파형의 평균 DC 값은 전체 기간(T) 동안의 모든 영역의 평균과 같습니다. 그러나 구형파의 양의 절반에 대한 총 면적은 동일한 구형파의 음의 절반의 면적과 정확히 동일하므로 순 면적은 0입니다. 즉, 음의 절반이 양의 절반을 상쇄하므로 대칭 구형파의 한 전체 주기(주기)에 대한 평균 값은 0이 됩니다.
그러나 파형의 양의 절반 또는 음의 절반의 평균값만으로는 0이 아닙니다. 따라서 이를 사용하여 사인파와 마찬가지로 반주기 동안만 구형파의 평균 값을 계산할 수 있습니다.
대칭 구형파의 양의 반주기에 대한 평균 전압 값 V ave 는 반 주기 동안 DC 전압을 효과적으로 나타내기 때문에 피크 또는 최대값 V max 와 같아야 합니다. 따라서: V ave = V max . 반파 정류 전압과 같은 비대칭 파형의 경우 평균값은 일반적으로 하나의 전체 사이클에 대해 사용됩니다.
또한 대칭 구형파의 순간 값은 항상 양의 피크 값인 +V p 또는 음의 피크 값인 -V p 와 같으므로 이 값의 제곱은 일정해야 합니다. 예를 들어, 임의의 시점에서 구형파의 순간 값을 취하면 크기가 항상 피크 값과 동일합니다. 따라서 이 값의 제곱은 다음과 같습니다: (Vp) 2 .
따라서 제곱평균제곱근 부분이 참이 되려면 전압 제곱의 평균(평균) 부분은 Vp 2 와 같습니다 . 따라서 이 평균값의 제곱근은 단순히 √ Vp 2 = V p 입니다 . 이는 대칭 구형파의 경우 피크 진폭과 RMS 값이 정확히 동일하므로 V rms = V p 입니다 .
따라서 피크(최대) 진폭, 평균값 및 RMS 값이 모두 동일한 경우 대칭 구형파의 파고율 (피크 대 평균 비율)은 간단히 다음과 같이 제공됩니다.

그러면 여기에서 대칭형 구형파의 파고율이 "1.0"(일치)이고 평평한 구형파 형태로 인해 피크, 평균 및 제곱 값이 동일하므로 단일 파고율을 기대할 수 있다는 것을 알 수 있습니다. . 그러나 펄스열과 같은 비대칭 구형파는 어떻습니까? 이들의 파고율을 어떻게 계산합니까?
펄스열 파고율
직사각형 펄스의 주기적인 시퀀스에 대한 파고율은 마크 대 공간 비율 이라고도 알려진 듀티 사이클로 정의됩니다 . 우리가 알고 있듯이, 하나의 전체 주기를 완료하는 데 걸리는 시간을 주기 시간 T 라고 합니다 .
일련의 펄스(펄스 트레인)의 경우 듀티 사이클은 일반적으로 백분율로 표시되는 전체 기간( T ON + T OFF )에 대한 온타임 T ON 의 비율입니다. 즉, 듀티 사이클은 주기에 대한 펄스 폭의 비율입니다. 그림과 같이 주기 = T = T ON + T OFF입니다 .
듀티 사이클 파형

예를 들어, 펄스의 온 타임이 12mS이고 주기가 60mS인 경우 듀티 사이클은 D = 12/60 = 0.2 또는 20% 입니다 . 마찬가지로 D = 45/60 = 0.75 또는 75% 듀티 사이클입니다. 즉, 펄스는 사이클 시간의 3/4 동안 "ON" 상태입니다.
확실히, 온 타임이 오프 타임과 같을 경우 ( T ON = T OFF ) 듀티 사이클은 0.5/1 = 0.5 또는 50%(1) 이므로 구형파 형태를 나타내는 50%가 됩니다 .
T ON 과 T OFF 의 비율 값이 서로 다르면 표시 대 공간 비율이 1이 아닌 결과가 됩니다. 그러면 펄스열의 듀티 사이클에 대한 일반화된 표현은 다음과 같습니다.

정현파의 파고율은 피크 값을 rms 값으로 나눈 값( V p /V rms )으로 제공되므로 듀티 사이클이 다양한 일련의 펄스에 대한 파고율은 다음과 같이 지정됩니다.
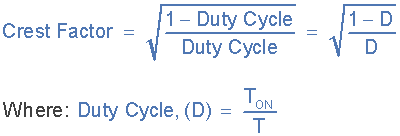
펄스열은 일정한 진폭을 가지므로 파고율 값에 가장 큰 영향을 미치는 것은 듀티 사이클입니다. 예를 들어, 그림과 같이 듀티 사이클 비율이 10%(0.1), 50%(0.5) 및 90%(0.9)라고 가정합니다.
펄스열 파고율

그러면 펄스열의 듀티 사이클이 10%에서 90%로 증가함에 따라 파고율이 3.0에서 0.33으로 감소하는 것을 볼 수 있습니다. 이는 10% 듀티 사이클에서 펄스 트레인이 일련의 매우 뾰족한 스파이크와 유사하기 때문입니다. 90%의 듀티 사이클은 플랫탑 상수 DC 공급의 듀티 사이클과 매우 유사합니다.
파고율 요약
이 튜토리얼에서 파고율은 RMS 값에 대한 파동 최대값 또는 피크 값의 비율이라는 것을 살펴보았습니다 . "파고율"이라는 용어는 전파의 특성과 완벽한 정현파와 얼마나 유사한지에 대한 정보를 제공하는 전파의 모양이나 구조를 나타냅니다. 연결된 부하가 전력 시스템에서 더 효율적으로 전력을 끌어오기 때문에 파고율 값이 낮을수록 더 좋습니다.
예를 들어, 전압 파고율 값은 전원 공급 장치의 전기 회로 부하를 나타냅니다. 전류 파고율 값은 부하가 전원 공급 장치의 전류를 소비하는 방식을 나타냅니다. 즉, 파고율 값이 높으면 큰 시스템 손실이 발생할 수 있으므로 파고율을 사용하여 연결된 부하 및/또는 무효 구성 요소가 전원 공급 네트워크의 전력 처리 기능에 어떤 영향을 미치는지 보여줄 수 있습니다.
앞서 살펴보았듯이 다양한 유형의 전기 파형은 정점에 따라 고유한 파고율 값을 가지며 정점이 높아질수록 파고율도 높아집니다. 대칭 구형파의 경우 파고율은 폼 팩터를 찾는 것과 동일한 RMS 및 피크 값을 갖기 때문에 "1"(단위)입니다 . 순수 사인파의 경우 파고율은 항상 1.414와 같습니다.
아래 표에는 위에서 설명한 다양한 종류의 파형에 대한 폼 팩터 공식과 값을 정의하는 표가 있습니다.
| 파형 유형 | 파고율 공식 | 값 |
| 사인파 | √ 2 | 1.414 |
| 반파 정류 사인파 | 2 | 2.0 |
| 전파 정류 사인파 | √ 2 | 1.414 |
| 삼각파형 | √ 3 | 1.732 |
| 톱니파형 | √ 3 | 1.732 |
| 대칭 구형파 | 1 | 1.0 |
'전자일기' 카테고리의 다른 글
| AC-DC 변환기 (0) | 2024.04.29 |
|---|---|
| 부울 대수학 단순화 (0) | 2024.04.29 |
| 555 회로 파트 2 (0) | 2024.04.02 |
| 555 회로 파트 1 (0) | 2024.04.02 |
| 555 발진기 튜토리얼 (0) | 2024.04.02 |