부울 대수학 단순화
부울 대수 단순화 및 변수, 리터럴 및 용어에 적용되는 몇 가지 기본 규칙을 사용하여 부울 대수 표현식을 단순화하는 방법
부울 대수학 단순화는 " + " 및 " 의 기호 또는 기호의 사용을 인식하면 이해하기 어렵지 않습니다 . ”는 논리 함수의 동작을 나타냅니다.
논리 함수는 조건 또는 상태가 TRUE 또는 FALSE 인지 여부를 테스트 하지만 동시에 둘 다는 아닙니다. 따라서 해당 테스트 결과에 따라 디지털 회로는 한 가지 작업 또는 다른 작업을 수행하기로 결정할 수 있습니다.
부울 대수의 법칙 튜토리얼 에서 보았듯이 부울 대수는 논리의 수학이며 다양한 전환 이론 규칙을 적용하면 길거나 복잡한 전환 대수 표기법을 단순화할 수 있으며 논리 게이트 및 논리 게이트에도 적용할 수 있습니다. 기본 디지털 회로.
그러나 부울 대수학이 보다 복잡한 스위칭 네트워크를 단순화하는 데 어떻게 도움이 될 수 있는지 알아보기 전에 먼저 AND , OR 및 NOT 의 세 가지 주요 기능과 관련된 몇 가지 기본 기호, 의미 및 법칙을 상기해 보겠습니다 .
논리 AND 연산
AND 연산자에 대해 제공된 논리 또는 부울 표현식은 논리 곱셈 또는 A와 B 의 부울 표현식이 A*B 와 동일한 부울 곱 에 대한 것입니다 . AND 연산자는 일반적으로 단일 점 또는 마침표 기호( . )로 표시됩니다. 이는 AB 또는 단순 AB 의 부울 표현식을 제공합니다 .
2입력 논리 AND 게이트

예를 들어, 입력 A, B, C가 있는 AND 게이트의 출력은 A x B x C(또는 ABC)로 작성되고 부울 곱 ABC는 "A 및 B 및 C"로 읽혀집니다.
그러나 ABC의 부울 곱은 CBA, A(BC) 또는 AB(C) 등으로 쓸 수도 있습니다. 이는 부울의 곱셈 결합 법칙을 따르는 것과 정확히 동일합니다.
그러면 두 개 이상의 입력 조건을 비교하고 모든 조건이 함께 발생하는 경우에만 TRUE를 반환하는 데 논리 AND 함수가 사용된다는 것이 분명합니다. 곱셈의 논리적 AND 연산은 직렬 연결된 스위치의 수에 관계없이 확장할 수 있으므로 스위치가 직렬로 연결되는 순서가 중요하지 않은 직렬 연결을 나타냅니다. 따라서 ABC의 부울 표현식은 대수 전환에서 다음과 같이 표시될 수 있습니다.
직렬(AND) 스위칭 표현

열린 스위치 조건을 "0"을 생성하는 비이벤트로 정의하고 스위치 폐쇄를 "1"을 생성하는 이벤트로 정의한다는 것을 기억하십시오. 또한 부울 표기법의 경우 두 개 이상의 유사한 용어를 "AND-ing"하면 부울의 멱등 법칙 에 따라 하나의 단일 용어가 생성됩니다 . 예: AA = A 또는 AAAA = A
논리 OR 연산
OR 연산자에 대해 제공된 논리 또는 부울 표현식은 A 또는 B 의 부울 표현식이 A+B 와 동일한 논리 합 또는 논리 합 에 대한 것입니다 . OR 연산자는 일반적으로 더하기 기호( + )로 표시되며 A+B 의 부울 표현식을 제공합니다 .
2입력 논리 OR 게이트
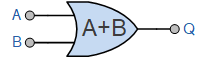
논리 OR 연산의 경우 세 개의 입력 A, B, C가 있는 경우 출력은 A + B + C로 작성되어 입력이 서로 추가되는 것을 보여줍니다. 부울 합계 A+B+C는 "A 또는 B 또는 C"로 읽히고 C+B+A 또는 B+A+C 또는 A+C+B 등으로 쓸 수도 있습니다. 이는 Boole의 덧셈 결합법칙을 따르는 것과 동일합니다.
그렇다면 논리 OR 함수는 두 개 이상의 입력 조건을 비교하는 데 사용되며 조건 중 하나가 발생하는 경우에만 TRUE를 반환한다는 것이 분명합니다. 추가의 논리적 OR 연산은 병렬 연결된 스위치의 수에 관계없이 확장할 수 있으므로 스위치가 병렬로 연결된 순서가 중요하지 않은 병렬 연결을 나타냅니다. 따라서 A+B+C의 부울 표현식은 대수 전환에서 다음과 같이 표시될 수 있습니다.
병렬(OR) 스위칭 표현
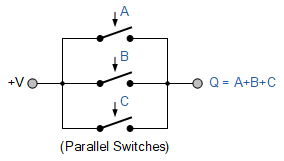
부울 표기법의 경우 두 개 이상의 유사한 용어를 "OR-ing"하면 다시 하나의 단일 용어가 생성됩니다. 이것이 바로 부울의 멱등 법칙 입니다 . 예: A+A = A 또는 A+A+A+A = A
논리 NOT 연산
논리적 NOT 연산은 단순히 부울 값의 반전 또는 보완 함수이며 별도의 변수로 간주되지 않습니다. NOT 함수는 출력 상태가 입력 상태와 "NOT"이고 일반적으로 반전 연산을 나타내는 기호 위에 막대 또는 윗줄( )로 표시되는 부울 표현식을 사용하여 그렇게 불립니다. 따라서 이름은 인버터입니다. .
즉, 스위치 A가 열려 있으면 A는 스위치가 닫혀 있다는 의미입니다. 즉, NOT 함수에 대한 부울 표현식은 입력이 "1"이면 출력이 "0"이고 입력이 "0"이면 출력이 "1"입니다.
부울 형식에서 반전은 보수 또는 반대 형식을 나타내는 A -bar 로 읽혀집니다. 또한 "이중 반전"( ̿ )은 두 개의 보완을 함께 나타냅니다. 이는 표현식을 변경하지 않고 표현식의 보수의 보수를 나타내기 때문에 A = A 입니다 . 이것이 원래의 표현(A)이다. 스위칭 회로에서 이 부정은 그림과 같이 일반적으로 닫힌 스위치로 표현될 수 있습니다.
표현이 아님
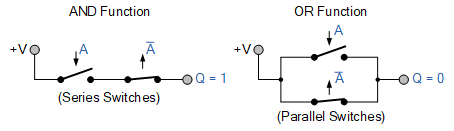
이중 반전 A , A 에 유의하세요 . A 와 A + A는 모두 부울의 보수 법칙을 나타냅니다 .
또한 부울 대수학에 관한 일부 책에서는 부울 값의 반전 또는 보완이 다음과 같이 표현됩니다. A' . 따라서 A 와 A'는 변수의 보수를 나타내기 위해 상호 교환적으로 사용될 수 있습니다.
부울 대수학 단순화
AND , OR 및 NOT 기능 의 전환 작업을 설정했습니다 . 이제 최소한의 항을 갖는 최종 표현식을 얻기 위해 몇 가지 기본 부울 대수 표현식을 단순화하는 방법을 살펴볼 수 있습니다.
먼저 다음과 같은 간단한 것부터 시작해 보겠습니다.
불리언 표현식: A.(A + B)
대괄호를 곱하면 다음과 같습니다.
| A.(A+B) | 시작 | |
| 곱하다: | AA + AB | 분배법칙 |
| 하지만: | AA = A | 멱등법칙 |
| 그 다음에: | A + AB | 절감 |
| 따라서: | A.(1 + B) | 무효화법 |
| 다음과 같습니다: | ㅏ | 흡수 법칙 |
그러면 A.(A + B)의 부울 표현이 부울의 흡수 법칙을 따르는 "A"로 축소될 수 있음을 알 수 있습니다 .
예시 2
이번에는 세 가지 부울 용어 A, B, C를 사용하고 이전과 동일한 부울 대수 단순화 규칙을 사용합니다.
부울 표현식: (A + B)(A + C)
다시, 괄호를 곱하면 다음과 같습니다.
| (A + B)(A + C) | 시작 | |
| 곱하다: | AA + AC + AB + BC | 분배법칙 |
| 하지만: | AA = A | 멱등법칙 |
| 그 다음에: | A + AC + AB + BC | 절감 |
| 하지만: | A + AC = A | 흡수 법칙 |
| 따라서: | A + AB + 기원전 | 분배법칙 |
| 다시: | A + AB = A | 흡수 법칙 |
| 따라서: | A + 기원전 | 결과 |
그런 다음 (A + B)(A + C)의 부울 표현은 다양한 부울 대수 법칙을 사용하여 "A + BC"로 축소될 수 있습니다.
부울 대수 단순화 예 No3
이번에는 A, B, C의 동일한 세 가지 부울 항을 다시 사용하지만 항 중 하나에 NOT 함수를 도입합니다.
불리언 표현: AB( B C + AC)
| AB( B C+AC) | 시작 | |
| 곱하다 | AB B .C + ABAC | 분배법칙 |
| 다시: | AA = A | 멱등법칙 |
| 그 다음에: | AB B .C + ABC | 절감 |
| 하지만: | B. B = 0 | 보완법 |
| 그래서: | A.0.C + ABC | 절감 |
| 다음과 같이 됩니다: | 0 + ABC | 절감 |
| 처럼: | 0 + ABC = ABC | 신원법 |
| 따라서: | 알파벳 | 결과 |
그런 다음 AB( B C+AC) 의 부울 표현은 "ABC"로 축소됩니다.
부울 대수 단순화 예 No4
이제 대수 표현을 가장 간단한 형태로 줄이기 위해 몇 가지 기본 부울 대수 법칙을 사용하여 부울 대수 용어를 단순화하는 방법에 대한 기본 아이디어를 갖게 되었습니다. 따라서 다음과 같은 마지막 부울 대수 단순화 예제 에서 모든 것을 하나로 묶습니다 .
불리언 표현식: (A + B + C )(A + B + C)(A + B + C )
다시 한번, 첫 번째 괄호를 곱하는 것부터 시작하겠습니다.
| (A+ B + C )(A+ B +C)(A+B+ C ) |
| A(A+ B +C)(A+B+ C ) + B (A+ B +C)(A+B+ C ) + C (A+ B +C)(A+B+ C ) |
| (AA+A B +AC)(AA+AB+A C ) + (A B + B B + B C )(A B +B B + B C ) + (A C + B C +C C )(A C +B C + C C ) |
| AA = A(멱등법칙) |
| B B = C C = 0 (보완법칙) |
| (A+A B +AC)(A+AB+A C ) + (A B + B + B C )(A B +0+ B C ) + (A C + B C +0)(A C +B 씨 + 씨 ) |
| A + AB = A (흡수 법칙) |
| A + AC = A (흡수 법칙) |
| A + 0 = A (동일성 법칙) |
| (A+AC)(A+AB+A C ) + (A B + B + B C )(A B + B C ) + (A C + B C )(A C +B C + C ) |
| A(A+AB+A C ) + ( B + B C )(A B + B C ) + (A C + B C )(B C + C ) |
| A(A+A C ) + B (A B + B C ) + C (A C + B C ) |
| AA + (A B + B B C ) + (A C C + B C C ) |
| A + (A B + B C ) + (A C + B C ) |
| A + (A B ) + ( B C ) + (A C ) |
| A + ( B C ) + ( A C ) |
| A + ( BC ) |
따라서 (A + B + C )(A + B + C)(A + B + C ) 의 복잡한 부울 표현식은 다음과 같은 더 작은 표현식으로 축소되었습니다. A + ( BC )
부울 대수 단순화 요약
우리는 이 부울 대수 단순화 튜토리얼에서 부울 대수 표현식을 단순화하는 목적이 최소 항 수를 갖는 최종 논리 표현식을 얻는 것임을 확인했습니다. 부울 함수는 AND, OR 및 NOT 연산자를 사용하여 형성된 대수식입니다.
A, B 및 C의 부울 변수는 함수의 리터럴 로 알려져 있으며 이 튜토리얼에서는 대문자 A, B 및 C를 사용했지만 리터럴은 기호 값을 가질 수 있습니다. 예를 들어 X,Y,Z 또는 a, b, c입니다. 따라서 모든 기호는 1 또는 0의 값을 가질 수 있는 논리 변수를 나타내는 데 사용될 수 있습니다.
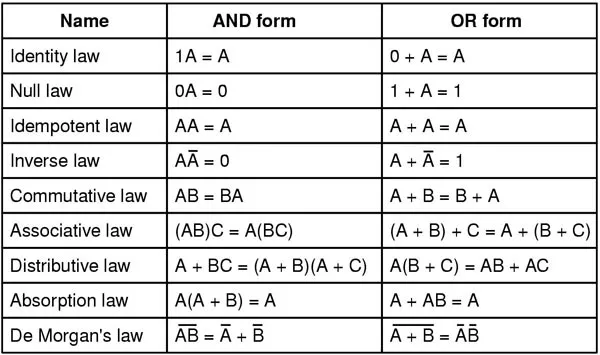
다음 부울 대수 단순화 표에 제시된 가장 일반적인 법칙을 사용하여 길거나 복잡한 표현 또는 조합 논리 회로를 훨씬 더 작은 회로로 줄이는 수단을 제공하는 여러 가지 부울 대수 법칙, 규칙 및 정리가 있습니다.
부울 대수 단순화 표
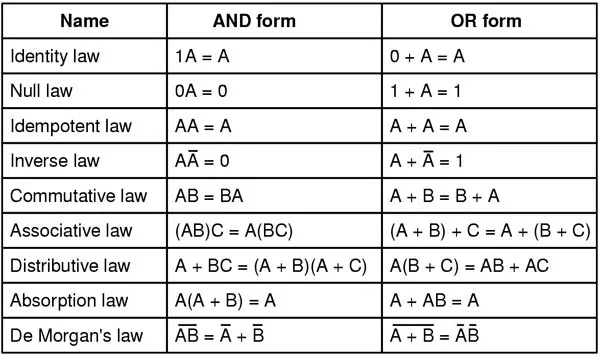
이러한 법률과 규칙 중 일부는 자명해 보일 수도 있고 그렇지 않은 경우도 있습니다. 조합 논리 회로 축소 또는 단순화 작업을 수행할 때 이들과 그 응용을 배우고 이해하는 것이 중요합니다.
그런 다음 부울 대수를 사용하여 모든 논리 회로를 원래 회로와 동일하게 기능하는 간단한 등가 회로로 줄일 수 있으며, 원래의 부울 표현식과 최종 부울 표현식의 동등성을 증명하기 위해 각각에 대해 비교할 진리표를 만들 수 있습니다. 진리표가 일치하면 최종 축소식이 올바른 것입니다.
'전자일기' 카테고리의 다른 글
| I 2 C 전압 레벨 변환기 (0) | 2024.04.30 |
|---|---|
| AC-DC 변환기 (0) | 2024.04.29 |
| 파형의 파고율 (0) | 2024.04.25 |
| 555 회로 파트 2 (0) | 2024.04.02 |
| 555 회로 파트 1 (0) | 2024.04.02 |