이진 분수
이진 분수는 각 이진수가 밑이 2인 숫자 체계를 사용한다는 점을 제외하면 십진수와 동일한 가중치 부여 원리를 사용합니다.
우리는 십진수(또는 디너리 ) 숫자가 십진수의 각 숫자가 0에서 9까지의 범위에서 가능한 10개의 값 중 하나를 취할 수 있는 10진수(10진수) 숫자 체계를 사용한다는 것을 알고 있습니다. 따라서 오른쪽에서 왼쪽으로 이동합니다. 십진수를 따라 각 숫자는 바로 오른쪽에 있는 숫자보다 10배 더 큰 값을 갖습니다.
그러나 오른쪽에서 왼쪽으로 움직일 때 각 숫자는 이전 숫자보다 10배 더 커질 뿐만 아니라, 왼쪽에서 오른쪽으로 반대 방향으로 움직일 때 각 숫자는 인접한 숫자보다 10배 더 작을 수도 있습니다. .
그러나 영(0)과 소수점에 도달하면 그냥 멈출 필요가 없으며 일반적으로 분수라고 불리는 숫자를 생성하는 숫자를 따라 왼쪽에서 오른쪽으로 계속 이동할 수 있습니다 .
일반적인 분수

이 십진수(또는 디너리) 숫자 예에서 소수점 바로 오른쪽에 있는 숫자(숫자 5)는 소수점 바로 왼쪽에 있는 숫자(숫자 4)의 10분의 1(1/10 또는 0.1)의 가치가 있습니다. ) 이는 1의 곱셈 값입니다.
따라서 숫자를 왼쪽에서 오른쪽으로 이동하면 이후의 각 숫자는 즉시 왼쪽 위치까지 숫자 값의 10분의 1이 됩니다.
그런 다음 십진수 체계에서는 위치 표기법을 생성하는 위치 또는 상대 가중치 개념을 사용합니다. 여기서 각 자릿수는 소수점 양쪽을 차지하는 위치에 따라 다른 가중치 값을 나타냅니다.
따라서 수학적으로 표준 디나리 숫자 체계에서 이러한 값은 일반적으로 위의 예에서 소수점 왼쪽의 각 위치에 대해 4 0 , 3 1 , 2 2 , 1 3 으로 작성됩니다. 마찬가지로, 소수점 오른쪽에 있는 분수의 경우 숫자의 가중치가 더 음수가 되어 5 -1 , 6 -2 , 7 -3 등이 됩니다.
따라서 표준 십진법의 각 숫자는 숫자 내에서 해당 숫자의 크기 또는 무게를 나타냅니다. 그러면 임의의 십진수의 값은 해당 자릿수에 해당 가중치를 곱한 값과 같게 됩니다. 따라서 위의 예에서는 N = 1234.567 10 가중 십진 형식에서 이 값도 동일합니다.
1000 + 200 + 30 + 4 + 0.5 + 0.06 + 0.007 = 1234.56710
또는 각 데너리 숫자의 가중치를 반영하도록 작성할 수도 있습니다.
(1×1000) + (2×100) + (3×10) + (4×1) + (5×0.1) + (6×0.01) + (7×0.001) = 1234.56710
또는 다음과 같은 다항식 형태로도 가능합니다.
(1×103) + (2×102) + (3×101) + (4×100) + (5×10-1) + (6×10-2) + (7×10-3) = 1234.56710
또한 각 숫자가 이진수 체계에서 차지하는 위치에 따라 서로 다른 가중치 값을 나타내는 위치 표기법 아이디어를 사용할 수도 있습니다. 이번에 차이점은 이진수 시스템(또는 간단히 이진수)이 위치 시스템이라는 것입니다. 여기서 숫자의 서로 다른 가중치 위치는 10이 아닌 2(밑 2)의 거듭제곱입니다.
이진 분수
이진수 체계는 "0" 또는 "1"의 두 자리 숫자만 포함하는 2진수 체계입니다. 따라서 이진수의 각 자릿수는 "0" 또는 "1" 값을 가질 수 있으며 0 또는 1의 위치는 해당 값 또는 가중치를 나타냅니다. 그러나 1보다 작은 값에 대해 이진 가중치를 적용하여 부호 없는 분수 이진수를 생성할 수도 있습니다.
소수 분수와 유사하게, 이진수는 소수점 오른쪽에 이진수를 배치하여 부호 없는 분수(이 경우에는 이진수)로 표시할 수도 있습니다. 따라서 이진수 오른쪽에 있는 모든 소수 자릿수는 2의 음의 거듭제곱인 각각의 가중치를 가지며 이진수를 생성합니다. 즉, 2의 거듭제곱은 음수입니다.
따라서 이진수 오른쪽에 있는 분수 이진수의 경우 각 숫자의 가중치는 표시된 대로 2 -1 , 2 -2 , 2 -3 , 2 -4 등으로 음수가 됩니다.
이진 분수

기타 등등
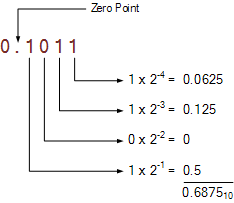
따라서 0.1011 2 의 이진 분수를 취하면 각 숫자의 위치 가중치가 고려되어 다음과 같은 십진수를 제공합니다.

이 예에서 이진수 0.1011 2 의 소수 변환은 0.6875 10 입니다 .
이진 분수 예 No1
이제 다음과 같은 이진수 1101.0111 2 가 있다고 가정해 보겠습니다 . 이에 해당하는 십진수는 얼마입니까?
1101.0111 = (1×23) + (1×22) + (0×21) + (1×20) + (0×2-1) + (1×2-2) + (1×2-3) + (1×2-4)
= 8 + 4 + 0 + 1 + 0 + 1/4 + 1/8 + 1/16
= 8 + 4 + 0 + 1 + 0 + 0.25 + 0.125 + 0.0625 = 13.437510
따라서 1101.0111 2 의 십진수는 다음과 같이 주어진다: 13.4375 10
따라서 우리는 분수 이진수, 즉 가중치가 1(2 0 ) 보다 작은 이진수는 이진수 가중치 인자를 각 감소에 대해 2의 값으로 연속적으로 나누어 해당 십진수로 변환할 수 있음을 알 수 있습니다. 2의 거듭제곱, 2 0은 0이 아니라 1과 같다는 것을 기억하세요.
기타 이진 분수의 예
0.11 = (1×2-1) + (1×2-2) = 0.5 + 0.25 = 0.7510
11.001 = (1×21) + (1×20) + (1×2-3) = 2 + 1 + 0.125 = 3.12510
1011.111 = (1×23) + (1×21) + (1×20) (1×2-1) + (1×2-2) + (1×2-3)
= 8 + 2 + 1 + 0.5 + 0.25 + 0.125 = 11.87510
소수를 이진 분수로 변환하기
소수를 이진 분수로 변환하는 것은 정수에 사용한 것과 유사한 방법을 사용하여 수행됩니다. 그러나 이 시간 곱셈은 소수의 소수 부분에 해당하는 이진수인 캐리 숫자를 사용하는 나머지 대신 정수로 나누는 대신 사용됩니다.
십진수에서 이진수로 변환할 때 십진수의 정수(오른쪽에서 왼쪽으로 양수) 부분과 분수(왼쪽에서 오른쪽으로 음수) 부분이 별도로 계산됩니다.
숫자의 정수 부분에 대해 해당 이진수는 소수의 정수 부분을 반복적으로 2(2)로 연속적으로 나누어(연속 나눗셈이라고 함) 구하며, 나머지는 최하위 비트(LSB)에서 역순으로 표시됩니다. )를 최상위 비트(MSB)로 변환하여 값이 "0"이 되어 해당 이진수를 생성합니다.
따라서 십진 정수에 해당하는 이진수를 찾으려면: 118 10
118 (2로 나누기) = 59 + 나머지 0 (LSB)
59 (2로 나누기) = 29 + 나머지 1 (↑)
29 (2로 나누기) = 14 + 나머지 1 (↑)
14 (2로 나누기) = 7 + 나머지 0 (↑)
7 (2로 나누기) = 3 + 나머지 1 (↑)
3 (2로 나누기) = 1 더하기 나머지 1 (↑)
1 (2로 나누기) = 0 + 나머지 1 (MSB)
그러면 118 10 에 해당하는 이진수는 다음과 같습니다. 1110110 2 ← (LSB)
숫자의 분수 부분은 소수의 주어진 분수 부분에 2(×2)를 반복적으로 곱하여(연속 곱셈으로 알려짐) 값이 이진수를 생성하는 "0"이 될 때까지 정방향 순서로 전달된다는 점에 유의하여 구합니다. 동등한.
따라서 곱셈 과정에서 1보다 큰 결과가 나오면 캐리는 "1"이 되고, 곱셈 과정에서 "1"보다 작은 결과가 나오면 캐리는 "0"이 됩니다.
또한 연속적인 곱셈 과정이 최종 0을 향하지 않는 것처럼 보이면 분수의 길이는 무한하거나 동등한 비트 수(예: 8비트)를 얻을 때까지 유지됩니다. 또는 16비트 등 필요한 정확도에 따라 달라집니다.
따라서 소수 분수에 해당하는 이진 분수를 찾으려면: 0.8125 10
0.8125 (2 곱하기) = 1 .625 = 0.625 캐리 1 (MSB)
0.625 (2 곱하기) = 1 .25 = 0.25 캐리 1 (↓)
0.25 (2 곱하기) = 0 .50 = 0.5 캐리 0 (↓)
0.5 (2 곱하기) = 1 .00 = 0.0 캐리 1 (LSB)
따라서 0.8125 10 에 해당하는 이진수는 다음과 같습니다. 0.1101 2 ← (LSB)
위 절차를 사용하여 이진 분수를 해당하는 십진수로 변환하면 이 답을 다시 확인할 수 있습니다. 0.1101 = 0.5 + 0.25 + 0.0625 = 0.8125 10
이진 분수 예 No2
다음 십진수에 해당하는 이진 분수를 찾으십시오: 54.6875
먼저 위에서 연속적인 나눗셈을 사용하여 일반적인 방법으로 정수 54를 이진수로 변환합니다.
54 (2로 나누기) = 27 나머지 0 (LSB)
27 (2로 나누기) = 13 나머지 1 (↑)
13 (2로 나누기) = 6 나머지 1 (↑)
6 (2로 나누기) = 3 나머지 0 (↑)
3 (2로 나누기) = 1 나머지 1 (↑)
1 (2로 나누기) = 0 나머지 1 (MSB)
따라서 54 10 에 해당하는 이진수는 다음과 같습니다. 110110 2
다음으로 연속 곱셈을 사용하여 소수 0.6875를 이진 분수로 변환합니다.
0.6875 (2 곱하기) = 1 .375 = 0.375 캐리 1 (MSB)
0.375 (2 곱하기) = 0 .75 = 0.75 캐리 0 (↓)
0.75 (2 곱하기) = 1 .50 = 0.5 캐리 1 (↓)
0.5 (2 곱하기) = 1 .00 = 0.0 캐리 1 (LSB)
따라서 0.6875 10 에 해당하는 이진수는 다음과 같습니다. 0.1011 2 ← (LSB)
따라서 십진수에 해당하는 이진수: 54.6875 10은 110110.1011 2 입니다 .
이진 분수 요약
우리는 이진 분수 에 대한 이 튜토리얼에서 소수 분수를 동등한 이진 분수로 변환하려면 소수 분수 부분과 소수 분수 부분만 2를 곱하고 이진수 왼쪽에 나타나는 숫자를 기록해야 한다는 것을 보았습니다. 가리키다. 캐리 숫자인 이 이진수는 항상 "0" 또는 "1"입니다.
그런 다음 나머지 소수 부분에 2를 다시 곱해야 하며, 분수가 0으로 줄어들거나 반복되는 이진 분수에 대해 필요한 양의 이진 비트가 완료될 때까지 연속적인 곱셈을 사용하여 위의 시퀀스를 다시 반복해야 합니다. 분수는 2의 음의 거듭제곱으로 표현됩니다.
혼합 십진수의 경우 두 가지 별도의 작업을 수행해야 합니다. 소수점 왼쪽의 정수부분은 연속적인 나눗셈, 소수점 오른쪽의 소수부분은 연속적인 곱셈을 합니다.
혼합 십진수의 정수 부분은 항상 정확한 이진수와 동일하지만 소수 부분은 그렇지 않을 수도 있습니다. 왜냐하면 소수 부분을 정확하게 표현하려는 경우 무한한 수의 이진수가 생성되는 반복 분수를 얻을 수 있기 때문입니다. .
'전자일기' 카테고리의 다른 글
| AC 회로의 전원 (0) | 2024.01.11 |
|---|---|
| 이진 코드 십진수 (1) | 2024.01.11 |
| AC 회로의 수동 부품 (0) | 2024.01.05 |
| harmonics/고조파/배음 아라보자 (1) | 2024.01.03 |
| 반응성 (3) | 2024.01.02 |