
AC 회로의 전원
AC 회로의 저항에 의해 소비되는 전력은 리액턴스가 에너지를 소비하지 않기 때문에 리액턴스에 의해 소비되는 전력과 다릅니다.
DC 회로에서 소비되는 전력은 단순히 DC 전압과 DC 전류를 곱한 값(와트 단위)입니다. 그러나 무효 부품이 있는 AC 회로의 경우 소비 전력을 다르게 계산해야 합니다.
전력은 회로에서 에너지가 소비되는 "비율"이므로 모든 전기, 전자 부품 및 장치는 안전하게 처리할 수 있는 전력량에 제한이 있습니다. 예를 들어 1/4와트 저항기 또는 20와트 증폭기입니다.
전력은 DC량 또는 AC량으로 시간에 따라 변할 수 있습니다. 임의의 순간에 회로의 전력량을 순간 전력 이라고 하며 전력은 볼트 곱하기 암페어(P = V*I)라는 잘 알려진 관계에 의해 제공됩니다. 따라서 1와트(초당 1줄의 에너지 소비율)는 1볼트에 1암페어를 곱한 것과 같습니다.
그러면 회로 요소에 의해 흡수되거나 공급되는 전력은 요소 전체의 전압 V와 회로 요소를 통해 흐르는 전류 I의 곱입니다. 따라서 저항이 "R" 옴인 DC 회로가 있는 경우 저항에 의해 소비되는 전력(와트)은 다음 일반 공식으로 제공됩니다.
전력

여기서 V 는 DC 전압, I 는 DC 전류, R 은 저항 값입니다.
따라서 전기 회로 내의 전력은 전압과 전류가 모두 존재할 때만 존재하며, 이는 개방 회로 또는 폐쇄 회로 조건이 아닙니다. 표준 저항성 DC 회로의 다음과 같은 간단한 예를 고려하십시오.
DC 저항 회로

AC 회로의 전력
DC 회로에서 전압과 전류는 일반적으로 일정하며, 이는 공급과 관련된 정현파 파형이 없기 때문에 시간에 따라 변하지 않습니다. 그러나 AC 회로의 전력의 경우 전압, 전류 및 그에 따른 전력의 순간 값은 공급 장치의 영향을 받아 지속적으로 변합니다. 따라서 DC 회로에서와 같은 방식으로 AC 회로의 전력을 계산할 수는 없지만 전력(p)은 전압(v)에 암페어(i)를 곱한 것과 같다고 말할 수 있습니다.
또 다른 중요한 점은 AC 회로에 리액턴스가 포함되어 있으므로 구성 요소에 의해 생성된 자기장 및/또는 전기장의 결과로 전력 구성 요소가 있다는 것입니다. 결과적으로 순수 저항성 구성 요소와 달리 이 전력은 저장되었다가 정현파 파형이 하나의 완전한 주기 주기를 통과할 때 전원으로 다시 반환됩니다.
따라서 회로에 의해 흡수되는 평균 전력은 저장된 전력과 완전한 한 사이클 동안 반환되는 전력의 합입니다. 따라서 회로의 평균 전력 소비는 순간 전력( p )과 순간 전압( v) 과 순간 전류( i ) 의 곱으로 정의되는 한 전체 사이클에 대한 순간 전력의 평균이 됩니다 . 사인 함수는 주기적이고 연속적이므로 전체 시간 동안 주어진 평균 전력은 단일 사이클 동안 주어진 평균 전력과 정확히 동일합니다.
전압과 전류의 파형이 모두 정현파라고 가정하면 다음을 기억할 수 있습니다.
정현파 전압 파형

AC 회로의 순간 전력은 특정 순간의 전력이므로 다음과 같습니다.

삼각함수 곱-합 항등식을 적용하면 다음과 같습니다.

θ = θ v – θ i (전압과 전류 파형 사이의 위상차)를 위의 방정식에 대입하면 다음과 같습니다 .

여기서 V 와 I 는 각각 정현파 파형 v 와 i 의 rms(평균 제곱근) 값 이고 θ는 두 파형 간의 위상차입니다. 따라서 AC 회로의 순간 전력은 다음과 같이 표현할 수 있습니다.
순간 방정식

이 방정식은 AC 회로의 순간 전력이 서로 다른 두 부분으로 구성되어 있으므로 이 두 항의 합이라는 것을 보여줍니다. 두 번째 항은 항의 2Ω 부분으로 인해 주파수가 공급 장치의 각 주파수의 두 배와 동일한 시변 정현파입니다. 그러나 첫 번째 항은 전압(V)과 전류(I) 사이의 위상차 θ에만 값이 의존하는 상수입니다.
AC 회로의 순간 전력은 시간이 지남에 따라 정현파의 프로파일에 따라 지속적으로 변하기 때문에 측정이 어렵습니다. 따라서 검정력의 평균 또는 평균값을 사용하는 것이 수학적으로 더 편리하고 쉽습니다. 따라서 고정된 수의 사이클에 걸쳐 정현파의 순간 전력의 평균값은 다음과 같이 간단하게 제공됩니다.

여기서 V 와 I 는 정현파 rms 값이고 θ (Theta)는 전압과 전류 사이의 위상각입니다. 전력의 단위는 와트(W)입니다.
AC 회로에서 소산된 전력은 그림과 같이 회로를 통해 흐르는 전압 V rms 또는 전류 I rms를 사용하여 회로의 임피던스(Z)에서도 찾을 수 있습니다.

튜토리얼 예제 No1
50Hz 정현파 공급 장치의 전압 및 전류 값은 각각 v t = 240 sin(Ωt +60 o )Volts 및 i t = 5 sin(Ωt -10 o )Amps로 지정됩니다. 순시 전력의 값과 회로가 흡수하는 평균 전력의 값을 구합니다.
위에서 회로에 의해 흡수되는 순간 전력은 다음과 같이 주어진다.

위의 삼각 항등 규칙을 적용하면 다음이 제공됩니다.

그러면 평균 전력은 다음과 같이 계산됩니다.
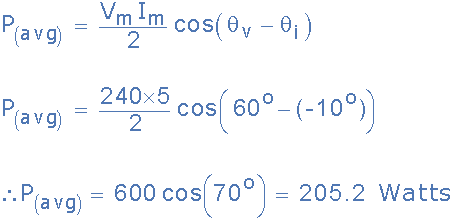
205.2와트의 평균 전력 값은 순간 전력 p (t) 의 첫 번째 항 값이기도 합니다. 이 첫 번째 항 상수 값은 소스와 부하 사이의 평균 또는 평균 에너지 변화율이기 때문입니다.
순수 저항성 회로
지금까지 우리는 DC 회로에서 전력은 전압과 전류의 곱과 동일하며 이 관계는 순수 저항성 AC 회로에도 적용된다는 것을 살펴보았습니다. 저항기는 에너지를 소비하는 전기 장치이며 저항기의 전력은 p = VI = I 2 R = V 2 /R로 지정됩니다. 이 힘은 언제나 긍정적이다.
그림과 같이 저항이 AC 공급 장치에 연결된 다음 순수 저항성(즉, 무한 커패시턴스, C = 및 0 인덕턴스, L = 0) 회로를 고려하십시오.
순수 저항성 회로
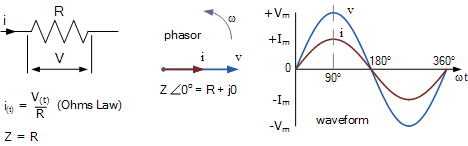
순수 저항기가 정현파 전압 공급 장치에 연결되면 저항기를 통해 흐르는 전류는 공급 전압에 비례하여 달라집니다. 즉, 전압과 전류 파형이 서로 "동위상"입니다. 전압 파형과 전류 파형의 위상차는 0o이므로 cos 0o가 되는 위상각은 1이 됩니다.
그러면 저항이 소비하는 전력은 다음과 같이 주어진다.
순수 저항기의 전력
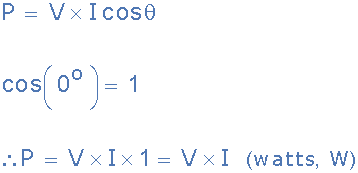
전압과 전류 파형이 동위상이므로, 즉 두 파형이 동시에 피크 값에 도달하고 동시에 0을 통과하므로 위의 전력 방정식은 V*I로 줄어듭니다. 따라서 두 파형을 곱하여 볼트-암페어 곱을 제공함으로써 특정 순간의 전력을 찾을 수 있습니다. 이를 "실제 전력"이라고 하며, ( P )는 와트(W), 킬로와트(kW), 메가와트(MW) 등으로 측정됩니다.
순수 저항기의 AC 파형
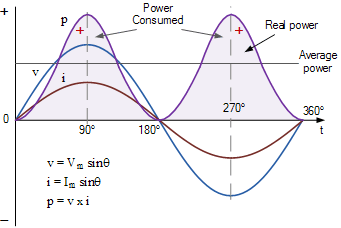
다이어그램은 전압, 전류 및 해당 전력 파형을 보여줍니다. 전압과 전류 파형이 모두 동위상이므로 양의 반주기 동안 전압이 양일 때 전류도 양이므로 양의 곱하기 양의 값은 양의 값과 같으므로 전력도 양의 값을 가집니다. 음의 반주기 동안 전압은 음이므로 전류는 음의 곱이 양의 값과 같으므로 양의 전력이 됩니다.
그런 다음 순수 저항성 회로에서는 전류가 저항기를 통해 흐르는 동안 항상 전력이 소비되며 다음과 같이 계산됩니다. P = V*I = I 2 R 와트. V와 I는 모두 rms 값일 수 있습니다. 여기서 V = I*R 및 I = V/R
AC 순수 유도 회로
L Henries의 순수 유도성(무한 커패시턴스, C = 및 저항 0, R = 0) 회로에서 전압 및 전류 파형은 동상이 아닙니다. 순수 유도성 코일에 변화하는 전압이 적용될 때마다 자체 인덕턴스로 인해 코일에 의해 "역" EMF가 생성됩니다. 이 자체 인덕턴스는 코일에 흐르는 전류의 모든 변화에 반대하고 제한합니다.
이 역기전력의 효과는 전류가 인가된 전압과 동위상인 코일을 통해 즉시 증가할 수 없기 때문에 전류 파형이 전압보다 어느 정도 시간이 지난 후 최고치 또는 최대값에 도달하게 된다는 것입니다. 결과적으로 순수 유도성 회로에서 전류는 표시된 것처럼 항상 전압보다 90o(π/2) 만큼 "지연"(ELI)됩니다.
순수 유도성 회로
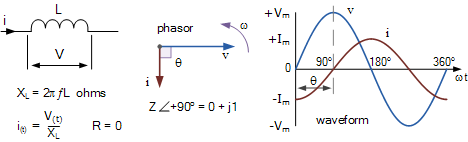
위의 파형은 순수 유도 코일 전체의 순간 전압과 순간 전류를 시간의 함수로 보여줍니다. 최대 전류, Imax 는 전압의 최대(피크) 값 이후 사이클의 1/4(90 ° )에서 발생합니다. 여기에서 전류는 전압 사이클 시작 시 음의 최대값으로 표시되고 전압 파형이 90o에서 최대값에 있을 때 0을 통과하여 양의 최대값으로 증가 합니다 .
따라서 전압 및 전류 파형은 더 이상 함께 상승 및 하강하지 않고 대신 90o(π/2)의 위상 변이가 코일 에 도입되므로 전압 및 전류 파형은 각각 "위상이 다릅니다". 다른 하나는 전압이 전류를 90o 앞서기 때문 입니다 . 전압 파형과 전류 파형의 위상차가 90o이므로 위상 각은 cos 90o = 0이 됩니다.
따라서 순수 인덕터에 의해 저장된 전력 QL은 다음 과 같이 주어진다.
순수 인덕터의 실제 전력
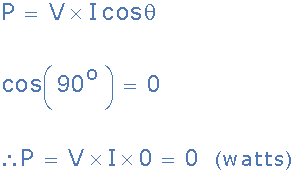
그렇다면 순수 인덕터는 실제 또는 실제 전력을 소비하거나 소비하지 않지만 전압과 전류가 모두 있으므로 다음 식에서 cos(θ)를 사용합니다. 순수 인덕터의 경우 P = V*I*cos(θ) 더 이상 유효하지 않습니다. 이 경우 전류와 전압의 곱은 일반적으로 "무효 전력"이라고 불리는 가상 전력이며, ( Q )는 반응 볼트 암페어(VAr), 킬로 볼트 암페어 반응(KVAr) 등으로 측정됩니다.
볼탐페레스 반응성 VAr을 실제 전력에 사용되는 와트(W)와 혼동해서는 안 됩니다. VAr은 서로 90 도 위상이 다른 볼트와 암페어의 곱을 나타냅니다 . 무효 평균 전력을 수학적으로 식별하기 위해 사인 함수가 사용됩니다. 그러면 인덕터의 평균 무효 전력 방정식은 다음과 같습니다.
순수 인덕터의 무효 전력
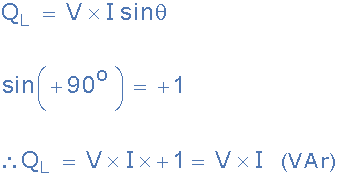
실제 전력(P)과 마찬가지로 무효 전력(Q)도 전압과 전류뿐 아니라 이들 사이의 위상각에 따라 달라집니다. 따라서 이는 적용된 전압과 표시된 대로 전압과 90o 위상차가 있는 전류의 구성 부분을 곱한 것 입니다 .
순수 인덕터의 AC 파형
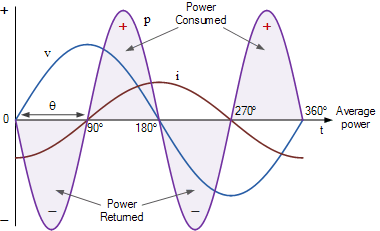
0 ° 와 90 ° 사이의 전압 파형의 양의 절반에서 인덕터 전류는 음이고 공급 전압은 양입니다. 따라서 볼트와 암페어 곱은 음의 곱과 양의 값이 음의 값과 같으므로 음의 전력을 제공합니다. 90o 와 180o 사이 에서 전류와 전압 파형 모두 값이 양수이므로 양의 전력이 발생합니다. 이 양의 전력은 코일이 공급 장치의 전기 에너지를 소비하고 있음을 나타냅니다.
180o 와 270o 사이 의 전압 파형의 음의 절반에는 음의 전압과 음의 전력을 나타내는 양의 전류가 있습니다. 이 음의 전력은 코일이 저장된 전기 에너지를 공급 장치로 다시 반환하고 있음을 나타냅니다. 270o 와 360o 사이 에서 인덕터 전류와 공급 전압은 모두 음이므로 양의 전력 기간이 발생합니다.
그런 다음 전압 파형의 한 전체 주기 동안 평균값이 0인 두 개의 동일한 양수 및 음수 전력 펄스가 있으므로 전력이 소스로 교대로 흐르기 때문에 실제 전력이 소모되지 않습니다. 이는 한 번의 전체 사이클 동안 순수 인덕터가 차지하는 총 전력이 0이므로 인덕터 무효 전력이 실제 작업을 수행하지 않음을 의미합니다.
순수 용량성 회로
C 패럿의 순수 용량성(즉, 인덕턴스가 0, L = 0이고 무한 저항, R = ) 회로는 전압 변화를 지연시키는 특성을 갖습니다. 커패시터는 유전체 내에 전기장의 형태로 전기 에너지를 저장하므로 순수 커패시터는 에너지를 낭비하지 않고 대신 저장합니다.
순수 용량성 회로에서는 커패시터 플레이트를 먼저 "충전"해야 하므로 전압은 전류와 동위상으로 증가할 수 없습니다. 이로 인해 전압 파형은 전류보다 일정 시간 후에 피크 또는 최대값에 도달하게 됩니다. 결과적으로 순수 용량성 회로에서는 전류가 항상 전압보다 90o(Ω/2) 앞서게 됩니다(ICE ) .
순수 용량성 회로
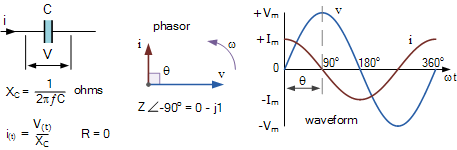
파형은 순수 커패시터의 전압과 전류를 시간의 함수로 보여줍니다. 최대 전류, Im은 전압의 최대(피크) 값 이전에 사이클의 1/4(90o ) 에서 발생합니다. 여기에서 전류는 전압 사이클 시작 시 양의 최대값으로 표시되고 0을 통과하며 전압 파형이 90 ° 에서 최대값에 있을 때 음의 최대값으로 감소합니다 . 순수 유도 회로로 반대 위상 이동.
따라서 순수 용량성 회로의 경우 위상각 θ = -90o 이고 커패시터의 평균 무효 전력 방정식은 다음과 같습니다.
순수 커패시터의 무효 전력
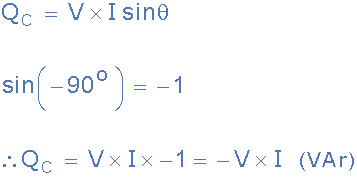
여기서 –V*I*sin(θ)는 음의 사인파입니다. 또한 용량성 무효 전력의 기호는 인덕터와 동일한 측정 단위인 VAR(볼트 암페어 무효 전력)을 사용하는 Q C 입니다. 그러면 위의 순수 유도성 회로와 마찬가지로 순수 커패시터는 실제 또는 유효 전력 P를 소비하거나 소모하지 않는다는 것을 알 수 있습니다.
순수 커패시터의 AC 파형
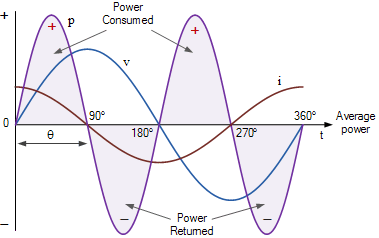
0 ° 와 90 ° 사이의 전압 파형의 양의 절반에서는 전류와 전압 파형 모두 양의 값을 가지므로 양의 전력이 소비됩니다. 90o 와 180o 사이 에서 커패시터 전류는 음이고 공급 전압은 여전히 양입니다. 따라서 볼트 암페어 곱은 음수 곱하기 양수가 음수와 같으므로 음의 전력을 제공합니다. 이 음의 전력은 코일이 저장된 전기 에너지를 다시 공급 장치로 되돌리고 있음을 나타냅니다.
180o 와 270o 사이 의 전압 파형의 음의 절반에서 커패시터 전류와 공급 전압 모두 값이 음수이므로 양의 전력 기간이 발생합니다. 이 양의 전력 기간은 코일이 공급 장치의 전기 에너지를 소비하고 있음을 나타냅니다. 270o 와 360o 사이 에는 다시 한번 음의 전력을 나타내는 음의 전압과 양의 전류가 있습니다.
그런 다음 전압 파형의 한 전체 주기 동안 평균 값이 0인 두 개의 동일한 양극 및 음극 전력 펄스가 있다는 점에서 순수 유도 회로의 경우와 동일한 상황이 존재합니다. 따라서 소스에서 커패시터로 전달되는 전력은 커패시터에 의해 소스로 반환되는 전력과 정확히 동일하므로 전력이 소스로 교대로 흐르기 때문에 실제 전력이 소모되지 않습니다. 이는 한 번의 전체 사이클 동안 순수 커패시터가 차지하는 총 전력이 0이므로 커패시터 무효 전력이 실제 작업을 수행하지 않음을 의미합니다.
튜토리얼 예제 No2
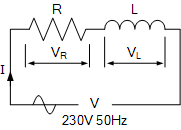
저항이 30Ω이고 인덕턴스가 200mH인 솔레노이드 코일은 230VAC, 50Hz 전원에 연결됩니다. 계산: (a) 솔레노이드 임피던스, (b) 솔레노이드에 의해 소비되는 전류, (c) 전류와인가 전압 사이의 위상각, (d) 솔레노이드에 의해 소비되는 평균 전력.
주어진 데이터: R = 30Ω, L = 200mH, V = 230V 및 f = 50Hz.
(a) 솔레노이드 코일의 임피던스(Z):
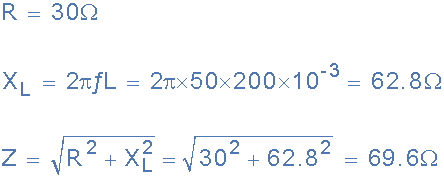
(b) 솔레노이드 코일이 소비하는 전류(I):
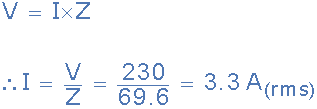
(c) 위상각, θ:
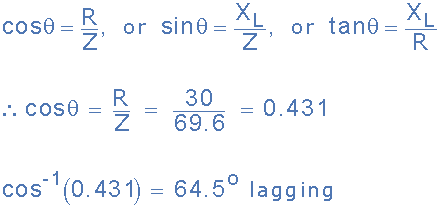
(d) 솔레노이드 코일이 소비하는 평균 AC 전력:
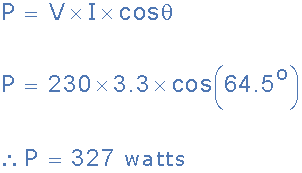
AC 전력 요약
우리는 여기서 AC 회로에서 순수 수동 회로에 흐르는 전압과 전류가 일반적으로 위상이 다르며 결과적으로 실제 작업을 수행하는 데 사용할 수 없음을 확인했습니다. 또한 직류(DC) 회로에서 전력은 전압에 전류를 곱한 것과 같거나 P = V*I와 같지만 필요에 따라 AC 회로와 동일한 방식으로 계산할 수는 없습니다. 위상차를 고려하십시오.
순수 저항성 회로에서 전류와 전압은 모두 동위상이며 모든 전력은 일반적으로 열의 형태로 저항에 의해 소비됩니다. 결과적으로 어떤 전력도 소스 공급 장치나 회로로 다시 반환되지 않습니다.
그러나 리액턴스를 포함하는 순수 유도성 또는 순수 용량성 회로에서는 (X) 전류가 전압을 정확히 90 ° (위상 각도)만큼 앞서거나 뒤처지므로 전력이 저장되고 다시 소스로 반환됩니다. 따라서 하나의 전체 주기 주기에 걸쳐 계산된 평균 전력은 0이 됩니다.
저항에 의해 소비되는 전력(R)은 실제 전력 또는 실제 전력이라고 하며 rms 전압과 rms 전류를 곱하여 간단히 얻습니다. 리액턴스(X)에 의해 저장된 전력을 무효 전력이라고 하며, 전압, 전류 및 이들 사이의 위상각의 사인을 곱하여 얻습니다.
위상각에 대한 기호는 θ(Theta)이며 이는 회로의 전류 흐름에 반대되는 총 무효 임피던스(Z)와 관련하여 AC 회로의 비효율성을 나타냅니다.
'전자일기' 카테고리의 다른 글
| 역률 보정 (0) | 2024.01.11 |
|---|---|
| 전력 삼각관계 및 역률 (0) | 2024.01.11 |
| 이진 코드 십진수 (1) | 2024.01.11 |
| 이진 분수 (1) | 2024.01.10 |
| AC 회로의 수동 부품 (0) | 2024.01.05 |