두 도시 사이의 거리를 설명해야 한다면 마일이나 킬로미터나 다른 선형 측정 단위로 된 단일 숫자로 답을 제공할 수 있습니다.
그러나 한 도시에서 다른 도시로 여행하는 방법을 설명하려면 두 도시 간의 거리뿐만 아니라 여행 방향 에 대한 정보도 제공해야 합니다 .
선형 거리와 같은 단일 차원을 표현하는 정보의 종류를 수학에서는 스칼라 양이라고 합니다. 스칼라 수는 지금까지 대부분의 수학적 응용 프로그램에서 사용한 종류의 숫자입니다.
예를 들어 배터리에서 생성되는 전압은 스칼라 양입니다. 전선의 저항 (옴)이나 전선을 통과하는 전류(암페어)도 마찬가지입니다.
그러나 교류 회로를 분석하기 시작하면 전압, 전류, 심지어 저항 ( 교류에서는 임피던스 라고 함 )의 양이 우리가 직류 회로에서 측정하던 익숙한 1차원 양이 아니라는 것을 알게 됩니다 .
오히려 이러한 양은 동적(방향과 진폭이 번갈아 가며)이기 때문에 고려해야 할 다른 차원을 가지고 있습니다. 주파수와 위상 변화는 이러한 차원 중 두 가지로 작용합니다.
단일 주파수만 다루는 비교적 간단한 AC 회로의 경우에도 진폭 외에도 위상 변화라는 차원을 고려해야 합니다.
AC 회로를 성공적으로 분석하려면 다차원 양을 표현할 수 있는 수학적 객체와 기술을 사용해야 합니다.
여기서 우리는 스칼라 수를 포기하고 더 적합한 것, 즉 복소수를 사용해야 합니다 . 한 도시에서 다른 도시로 가는 길을 알려주는 예와 마찬가지로, 단일 주파수 회로의 AC 양은 진폭(비유: 거리)과 위상 이동 (비유: 방향)을 모두 갖습니다.
복소수는 진폭과 위상 변화의 두 차원을 동시에 표현할 수 있는 단일한 수학적 양입니다.
복소수의 그래픽 표현
복소수는 그래픽으로 표현하면 이해하기가 더 쉽습니다. 특정 길이(크기)와 각도(방향)로 선을 그리면, 물리학에서 일반적으로 벡터 로 알려진 복소수의 그래픽 표현이 생깁니다 . (아래 그림)
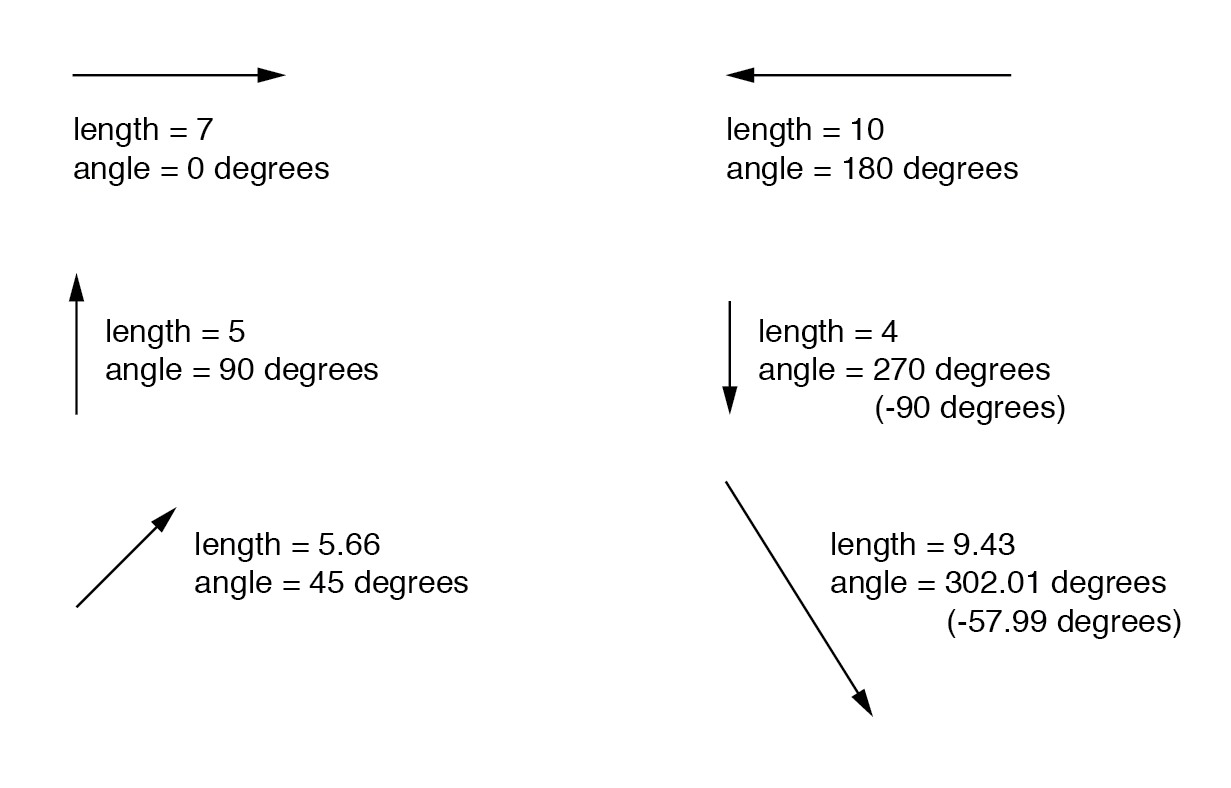
지도에서 거리와 방향처럼 각도 수치가 어떤 의미를 갖기 위해서는 공통된 기준 프레임이 있어야 합니다. 이 경우, 직각은 0 o 로 간주되고 각도는 시계 반대 방향으로 양의 방향으로 계산됩니다. (아래 그림)

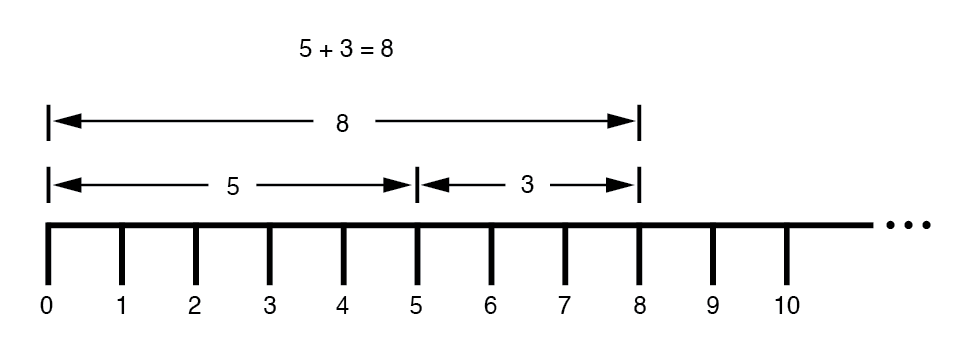
숫자를 그래픽 형태로 표현하는 아이디어는 새로운 것이 아닙니다. 우리 모두는 초등학교에서 "숫자선"으로 이것을 배웠습니다. (아래 그림)

우리는 길이(크기)가 어떻게 쌓여 최종 답을 얻는지 보면서 덧셈과 뺄셈이 어떻게 작동하는지 배웠습니다. (아래 그림)
나중에, 우리는 선에 표시된 정수 사이의 값을 지정하는 방법이 있다는 것을 알게 되었습니다 . 이는 분수 또는 소수 양이었습니다. (아래 그림)

초등학교에서 배우는 이러한 숫자 필드(전체, 정수, 유리수, 무리수, 실수 등)는 공통적인 특성을 공유합니다. 모두 1차원 입니다 . 숫자선의 직선성은 이를 그래픽으로 보여줍니다.
숫자선을 따라 위아래로 움직일 수 있지만, 해당 선을 따라 움직이는 모든 "움직임"은 단일 축(수평)으로 제한됩니다.
1차원 스칼라 수는 구슬을 세거나, 무게를 나타내거나, DC 배터리 전압을 측정하는 데는 적합하지만, 두 도시 간의 거리 와 방향, AC 파형의 진폭 과 위상 과 같이 더 복잡한 것을 나타내기에는 부족합니다 .
이런 종류의 양을 표현하려면 다차원 표현이 필요합니다. 다시 말해, 서로 다른 방향을 가리킬 수 있는 숫자선이 필요하고, 그것이 바로 벡터입니다.
검토:
- 스칼라 수란 사람들이 일상생활에서 사용하는 수학적 객체의 한 유형입니다. 즉, 온도, 길이, 무게 등과 같은 1차원 양입니다 .
- 복소수 는 크기와 방향의 두 차원을 나타내는 수학적 양입니다.
- 벡터 는 복소수의 그래픽 표현입니다. 시작점, 팁, 명확한 길이, 명확한 방향이 있는 화살표처럼 보입니다. 때때로 위상수라는 단어는 벡터의 각도가 파형 간의 위상 변화를 나타내는 전기 응용 분야에서 사용됩니다.