전자일기

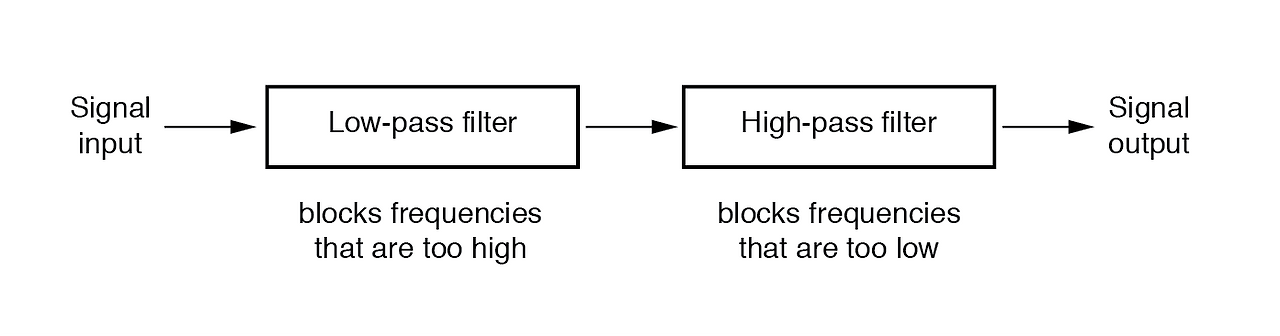
지금까지 우리가 집중한 필터 설계는 커패시터나 인덕터를 사용했지만 ,  두  가지 를 동시에 사용한 적은 없습니다. L과 C의 조합은 공진하는 경향이 있으며, 이 속성은  대역 통과 및  대역 저지 필터 회로를 설계하는 데 활용할 수 있다는 것을 이제 알았을 것입니다.직렬 LC 회로는 공진에서 최소 임피던스를 제공하는 반면,  병렬 LC("탱크") 회로는 공진 주파수에서 최대 임피던스를 제공합니다. 이를 알고 있으므로 대역 통과 또는 대역 저지 필터를 설계하기 위한 두 가지 기본 전략이 있습니다.대역 통과 필터의 경우 두 가지 기본 공진 전략은 다음과 같습니다. 신호를 통과시키는 직렬 LC 또는 신호를 단락시키는 병렬 LC. 두 가지 방식을 여기에서 대조하고 시뮬레이션합니다.시리즈 공진 대역 통과 필터직..

대역저지 필터를 만드는 방법은?대역 제거 필터 , 대역 제거 필터 또는 노치 필터 라고도 하는 이 종류의 필터는 구성 요소 값에 의해 설정된 특정 범위 위아래의 모든 주파수를 통과시킵니다. 놀랍지 않게도  대역 통과 설계 와 마찬가지로  저역 통과 필터 와  고역 통과 필터로 만들 수 있지만 이번에는 두 필터 섹션을 직렬이 아닌 병렬로 연결합니다. 대역저지 필터의 시스템 수준 블록 다이어그램. Twin-T 대역 차단 필터두 개의 용량성 필터 섹션을 사용하여 제작되었으며 다음과 같습니다. "트윈-T" 대역 차단 필터. 저역 통과 필터 섹션은 "T" 구성의 R 1 , R 2 , C 1 로 구성됩니다. 고역 통과 필터 섹션도 "T" 구성의 C 2 , C 3 , R 3 로 구성됩니다 . 이러한 배열은 일반적으로..

대역 통과 필터를 만드는 방법특정 대역 또는 스프레드 또는 주파수를 더 넓은 범위의 혼합 신호에서 필터링해야 하는 애플리케이션이 있습니다.  필터 회로는 저역 통과 및 고역 통과의 속성을 단일 필터로 결합하여 이 작업을 수행하도록 설계할 수 있습니다. 그 결과를 대역 통과 필터 라고 합니다 .저역통과 필터와 고역통과 필터에서 대역통과 필터를 만드는 방법은 블록 다이어그램을 사용하여 설명할 수 있습니다. 대역 통과 필터의 시스템 수준 블록 다이어그램. 커패시터를 사용한 대역 통과 필터 설계이 두 필터 회로의 직렬 조합 에서 나오는 것은  너무 높지도 낮지도 않은 주파수만 통과시키는 회로입니다. 실제 구성 요소를 사용하면 일반적인 회로도는 다음과 같습니다. 대역 통과 필터의 응답은 다음과 같습니다. 용량성 ..

고역 통과 필터의 작업은 저역 통과 필터의 정반대입니다. 즉, 고주파 신호는 쉽게 통과시키고 저주파 신호는 통과시키기 어렵게 하는 것입니다. 예상할 수 있듯이, 고역 통과 필터의 유도성(아래 그림) 및 용량성(아래 그림) 버전은 각각의 저역 통과 필터 설계와 정반대입니다. 용량성 고역통과 필터. 커패시터의 임피던스커패시터의 임피던스(위 그림)는 주파수가 감소함에 따라 증가합니다.(아래 그림) 직렬로 연결된 이러한 높은 임피던스는 저주파 신호가 부하에 도달하는 것을 차단하는 경향이 있습니다. 용량성 고역 통과 필터 v1 1 0 ac 1 sin 씨1 1 2 0.5유 rload 2 0 1k .ac 린 20 1 200 .플롯 ac v(2) .끝 용량성 고역통과 필터의 응답은 주파수에 따라 증가합니다. 유도성 고..

정의에 따르면 저역통과 필터는 저주파 신호에는 쉽게 통과시키고 고주파 신호에는 통과시키기 어려운 회로입니다. 이 목적을 달성할 수 있는 두 가지 기본 회로가 있으며, 각각에 대한 많은 변형이 있습니다. (아래 그림)의 유도성 저역통과 필터와 (아래 그림)의 용량성 저역통과 필터입니다.유도 저역통과 필터 유도 저역통과 필터 인덕터의 임피던스는 주파수가 증가함에 따라 증가합니다. 직렬로 연결된 이 높은 임피던스는 고주파 신호가 부하에 도달하는 것을 차단하는 경향이 있습니다. 이는 SPICE 분석으로 입증할 수 있습니다. (아래 그림) 유도 저역통과 필터 v1 1 0 ac 1 sin l1 1 2 3 rload 2 0 1k .ac 린 20 1 200 .플롯 ac v(2) .끝 유도성 저역통과 필터의 응답은 주파..

때로는 회로에서 다양한 주파수의 혼합에서 하나의 주파수 또는 주파수 범위를 선택적으로 필터링할 수 있는 회로를 갖는 것이 바람직합니다. 이 주파수 선택을 수행하도록 설계된 회로를 필터 회로 또는 간단히 필터 라고 합니다 .필터 회로는 일반적으로 고성능 스테레오 시스템에서 필요한데, 최적의 음질과 전력 효율을 위해 특정 범위의 오디오 주파수를 증폭하거나 억제해야 하기 때문입니다.여러분은 이퀄라이저 에 대해 알고 있을 것입니다 . 이퀄라이저는 청취자의 취향과 청취 공간의 음향 특성에 맞춰 여러 주파수 범위의 진폭을 조절할 수 있게 해줍니다.또한 , 특정 주파수 범위가 스피커에 도달하지 못하도록 차단하는 크로스오버 네트워크 에 대해서도 알고 계실 것입니다 .트위터(고주파 스피커)는 드럼 비트와 같은 저주파 신..

비정현파의 반복적 파형이 서로 다른 주파수의 일련의 정현파와 동일하다는 원리 는 일반적으로 파동의 기본 속성이며 교류 회로를 연구하는 데 매우 실용적으로 중요합니다.이는 완벽한 사인파 모양이 아닌 파형이 있을 때마다 해당 회로는 마치 서로 다른 주파수 전압의 배열이 동시에 인가된 것처럼 반응한다는 것을 의미합니다.AC 회로가 주파수의 혼합으로 구성된 소스 전압에 노출되면 해당 회로의 구성 요소는 각 구성 주파수에 다른 방식으로 응답합니다. 커패시터나 인덕터와 같은 모든 반응성 구성 요소는 동시에 회로에 존재하는 각 주파수에 고유한 양의 임피던스를 나타냅니다.다행히도 이러한 회로의 분석은 중첩 정리를 적용함으로써 비교적 쉽게 이루어질 수 있습니다. 중첩 정리는 다중 주파수 소스를 직렬로 연결된 단일 주파수..

특히 FFT 알고리즘 형태의 컴퓨터화된 푸리에 분석은 파형 과 관련 스펙트럼 구성 요소 에 대한 이해를 높이는 데 강력한 도구입니다 .SPICE 시뮬레이터 에 .fourier 옵션으로 프로그래밍된 이 동일한 수학적 루틴은 다양한 전자 테스트 장비에도 프로그래밍되어 측정된 신호에 대한 실시간 푸리에 분석을 수행합니다.이 섹션에서는 이러한 도구의 사용과 여러 가지 파형의 분석에 대해 설명합니다.먼저 523.25Hz 주파수의 간단한 사인파가 있습니다. 이 특정 주파수 값은 피아노 건반의 "C" 피치로, "중간 C"보다 한 옥타브 높습니다.사실, 이 데모를 위해 측정된 신호는 팬 플루트의 음색을 내도록 설정된 전자 키보드에 의해 생성되었습니다. 팬 플루트는 제가 완벽한 사인파와 비슷한 가장 가까운 악기 "음성"..

이상하게 보일지 몰라도, 반복 되는 비정현파 파형 은 실제로 서로 다른 진폭과 주파수의 일련의 정현파 파형을 합친 것과 같습니다. 사각파는 매우 흔하고 잘 알려진 사례이지만 유일한 사례는 아닙니다.트랜지스터 및 실리콘 제어 정류기( SCR ) 와 같은 전자 전력 제어 장치는 종종 전원 공급 장치 의 "깨끗한"(순수한) 사인파 AC를 본질적으로 잘게 자른 버전인 전압 및 전류 파형을 생성합니다 .이러한 장치는 제어 신호 전압 또는 전류를 인가하면 갑자기 저항을 변경할 수 있어 거의 즉시 "켜지거나" "꺼지며" 회로에 전원을 공급하는 소스 전압 파형과 거의 유사한 전류 파형을 생성합니다.이러한 전류 파형은 회로 임피던스를 통과하는 비정현파 전류에 의해 발생한 전압 강하로 인해 다른 회로 구성 요소에 대한 전..

반복 적이고 비정현파는 다양한 진폭과 주파수에서 DC 전압, 사인파 및/또는 코사인파(90도 위상 편이를 갖는 사인파)의 조합으로 표현될 수 있다는 것이 밝혀졌습니다 .이는 문제의 파형이 아무리 이상하거나 복잡하더라도 사실입니다 . 시간이 지남에 따라 규칙적으로 반복되는 한, 이 일련의 사인파로 축소될 수 있습니다.특히, 사각파는 같은 주파수의 사인파와 감소하는 진폭의 무한한 홀수-배수 주파수 사인파 시리즈의 합과 수학적으로 동일하다는 것이 밝혀졌습니다.  파형에 대한 이 진실은 처음에는 믿기 어려울 정도로 이상하게 보일 수 있습니다. 그러나 사각파가 실제로 사인파 고조파의 무한한 시리즈를 더한 것이라면, 여러 사인파 고조파를 더하여 사각파에 가까운 근사값을 만들어내어 이를 증명할 수 있어야 한다는 것은..