
정전 용량 및 전하
커패시터는 전기 에너지를 전하의 형태로 플레이트에 저장합니다.
커패시턴스는 커패시터가 전하를 저장하는 능력을 측정한 값입니다. 이 커패시턴스 값은 두 개의 평행판을 분리하는 데 사용되는 유전 물질의 유전 상수에 따라 달라집니다. 커패시턴스는 패럿 (F) 단위로 측정되며 , 마이클 패러데이(Michael Faraday) 의 이름을 따서 명명되었습니다 .
커패시터는 두 개의 평행한 전도성 판(보통 금속)으로 구성되며, 이 판은 "유전체"라고 불리는 절연 물질에 의해 서로 닿는 것(분리된 것)이 방지됩니다. 이들 플레이트에 전압이 가해지면 전류가 흘러 한 플레이트는 공급 전압에 대해 양전하로 충전되고 다른 플레이트는 동일하고 반대되는 음전하로 충전됩니다.
그러면 커패시터는 전자의 전하 Q ( 쿨롱 단위 )를 저장할 수 있는 능력을 갖습니다. 커패시터가 완전히 충전되면 플레이트 사이에 전위차(pd)가 있으며, 플레이트의 면적이 클수록 및/또는 플레이트 사이의 거리(분리라고도 함)가 작을수록 커패시터가 전하는 더 많이 충전됩니다. 보유할 수 있고 커패시턴스 가 커질 것입니다 .
플레이트 사이에 이 전하( Q )를 저장하는 커패시터의 능력 은 알려진 정전용량(패럿)을 갖는 커패시터의 인가 전압 V 에 비례합니다. 커패시턴스 C 는 항상 양수이며 음수는 아닙니다.
인가된 전압이 클수록 커패시터 플레이트에 저장된 전하도 커집니다. 마찬가지로 인가 전압이 작을수록 전하는 작아집니다. 따라서 커패시터 플레이트의 실제 전하 Q는 다음과 같이 계산할 수 있습니다.
커패시터의 충전

여기서: Q (전하, 쿨롱) = C (커패시턴스, 패럿) x V (전압, 볼트)
때로는 그림을 사용하여 이 관계를 기억하는 것이 더 쉽습니다. 여기서 Q , C 및 V 의 세 가지 양은 삼각형으로 겹쳐져 상단에 전하를 제공하고 하단에 커패시턴스와 전압을 제공합니다. 이 배열은 커패시터 충전 공식 에서 각 수량의 실제 위치를 나타냅니다 .
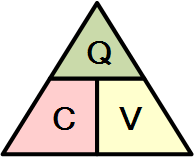
위의 방정식을 전치하면 동일한 방정식의 다음 조합이 제공됩니다.

단위: Q는 쿨롱, V 는 볼트, C는 패럿으로 측정됩니다.
그런 다음 위에서부터 커패시턴스 단위를 Farad 단위 F 라고도 하는 쿨롱/볼트와 동일한 비례 상수로 정의할 수 있습니다 .
커패시턴스는 플레이트에 전하를 저장하는 커패시터의 능력(용량)을 나타내기 때문에 1패럿을 " 플레이트 사이에 1볼트의 전위차를 설정하기 위해 1쿨롱의 전하가 필요한 커패시터의 커패시턴스 "로 정의할 수 있습니다. 마이클 패러데이(Michael Faraday)가 설명했습니다. 따라서 커패시턴스가 클수록 동일한 양의 전압에 대해 커패시터에 저장되는 전하량이 높아집니다.
전도성 플레이트에 전하를 저장하는 커패시터의 능력은 커패시터의 커패시턴스 값을 제공합니다. 커패시턴스는 또한 플레이트의 치수나 면적, A 및 플레이트 사이의 유전 물질의 특성으로부터 결정될 수 있습니다. 유전 물질의 측정은 유전율( ε ) 또는 유전 상수로 제공됩니다. 따라서 커패시터의 커패시턴스를 표현하는 또 다른 방법은 다음과 같습니다.
공기를 유전체로 하는 커패시터
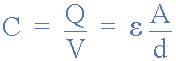
고체를 유전체로 사용하는 커패시터
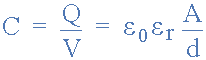
A 는 플레이트의 면적(제곱미터)이며, 면적이 클수록 커패시터가 저장할 수 있는 전하의 양은 더 많아집니다. d 는 두 판 사이의 거리 또는 간격입니다.
이 거리가 작을수록 플레이트의 전하 저장 능력이 더 높아집니다. 왜냐하면 -Q 대전 플레이트의 -ve 전하가 +Q 대전 플레이트에 더 큰 영향을 미쳐 +에서 더 많은 전자가 반발되기 때문입니다. Q 충전 플레이트로 인해 전체 전하가 증가합니다.
ε 0 (엡실론)은 8.854 x 10 -12 F/m 인 공기의 유전율 값이고 , ε r 은 두 플레이트 사이에 사용되는 유전체 매체의 유전율입니다.
평행판 커패시터
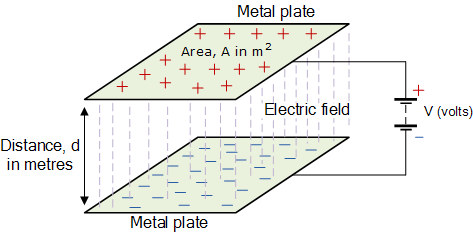
이전에 평행판 커패시터의 커패시턴스는 표면적 A 에 비례하고 두 판 사이의 거리 d 에 반비례한다고 말했으며 이는 공기의 유전 매체에 해당됩니다. 그러나 커패시터의 정전 용량 값은 공기보다 유전 상수가 큰 전도성 판 사이에 고체 매체를 삽입하여 증가시킬 수 있습니다.
일반적으로 사용되는 다양한 유전체 재료에 대한 엡실론 ε 의 일반적인 값은 다음과 같습니다. 공기 = 1.0, 종이 = 2.5 – 3.5, 유리 = 3 – 10, 운모 = 5 – 7 등.
유전 물질 또는 절연체가 공기에 비해 커패시터의 커패시턴스를 증가시키는 요인을 유전 상수 ( k )라고 합니다. "k" 는 사용되는 유전 매체의 유전율과 진공이라고도 알려진 자유 공간의 유전율의 비율입니다.
따라서 모든 커패시턴스 값은 진공 유전율과 관련이 있습니다. 유전 상수가 높은 유전 물질은 유전 상수가 낮은 유전 물질보다 더 나은 절연체입니다. 유전 상수는 자유 공간에 상대적이므로 무차원 양입니다.
커패시턴스 예 No1
평행판 커패시터는 총 표면적이 100 cm 2 인 두 개의 판으로 구성됩니다 . 플레이트 간격이 0.2 cm이고 사용된 유전 매체가 공기인 경우 커패시터의 정전 용량(피코 패럿(pF))은 얼마입니까?

그러면 커패시터의 값은 44pF입니다.
커패시터의 충전 및 방전
다음 회로를 고려하십시오.
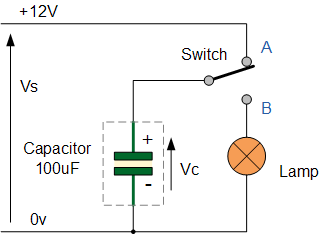
커패시터가 완전히 방전되었고 커패시터에 연결된 스위치가 A 위치로 이동했다고 가정합니다 . 이 시점에서 100uf 커패시터 양단의 전압은 0이고 충전 전류( i )가 플레이트 양단의 전압이 12v 공급 전압과 거의 동일할 때까지 기하급수적으로 커패시터를 충전하기 시작합니다. 5개의 시정수가 지나면 전류는 조금씩 충전되고 커패시터는 "완전 충전"되었다고 합니다. 그러면 VC = VS = 12볼트 입니다 .
이론적으로 커패시터가 "완전 충전"되면 일종의 임시 저장 장치 역할을 하므로 공급 전압이 끊어지더라도 전압 충전 상태를 유지합니다. 그러나 이것이 "이상적인" 커패시터의 경우에는 해당될 수 있지만, 실제 커패시터는 유전체를 통해 흐르는 내부 누설 전류로 인해 오랜 시간에 걸쳐 천천히 스스로 방전됩니다.
고전압 공급 장치에 연결된 큰 값의 커패시터는 공급 전압이 "OFF"로 전환된 경우에도 여전히 상당한 양의 전하를 유지할 수 있으므로 기억해야 할 중요한 사항입니다.
이 시점에서 스위치가 분리되면 커패시터는 전하를 무한정 유지하지만 유전체를 통해 흐르는 내부 누설 전류로 인해 전자가 유전체를 통과할 때 커패시터는 매우 천천히 방전되기 시작합니다. 커패시터가 공급 전압의 37%까지 방전되는 데 걸리는 시간을 시상수라고 합니다 .
이제 스위치가 위치 A 에서 위치 B 로 이동 하면 완전히 충전된 커패시터는 이제 연결된 램프를 통해 방전되기 시작하고 램프 요소에 저항 값이 있으므로 커패시터가 완전히 방전될 때까지 램프를 비춥니다.
램프의 밝기와 조명 지속 시간은 궁극적으로 커패시터의 커패시턴스 값과 램프의 저항( t = R*C )에 따라 달라집니다. 커패시터의 값이 클수록 더 많은 전하를 저장할 수 있으므로 램프 조명이 더 밝고 길어집니다.
커패시턴스 예 No2
위 커패시터 회로의 전하를 계산하십시오.
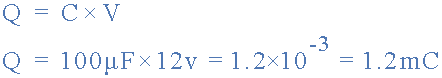
커패시터를 통한 전류
두 플레이트 사이의 유전 물질의 절연 특성으로 인해 저항기나 인덕터처럼 전류가 실제로 커패시터를 통해 흐를 수 없습니다. 그러나 두 판의 충전과 방전은 전류가 흐르는 효과를 준다.
전류는 시간에 따른 전하의 흐름 속도이므로 커패시터를 통해 흐르는 전류는 플레이트의 전하와 직접적인 관련이 있습니다. 플레이트 사이에 전하( Q ) 를 저장하는 커패시터의 능력은 인가 전압( V )에 비례하므로 전류와 커패시터 플레이트에 인가되는 전압 사이의 관계는 다음과 같습니다.
전류-전압(IV) 관계
시간이 지남에 따라 플레이트 양단의 전압이 증가(또는 감소)함에 따라 커패시턴스를 통해 흐르는 전류는 인가된 전압에 비례하는 전하량으로 플레이트에서 전하를 증착(또는 제거)합니다. 그러면 커패시턴스에 적용되는 전류와 전압은 모두 시간의 함수이며 i (t) 및 v (t) 기호로 표시됩니다 .
그러나 위의 방정식에서 전압이 일정하게 유지되면 전하도 일정해지고 따라서 전류는 0이 된다는 것을 알 수 있습니다. 즉, 전압의 변화가 없고 전하의 이동도 없으며 전류의 흐름도 없습니다. 이것이 바로 커패시터가 안정된 DC 전압에 연결될 때 전류 흐름을 "차단"하는 것처럼 보이는 이유입니다.
커패시턴스 값 - 패러드
이제 우리는 전하를 저장하는 커패시터의 능력이 커패시터에 패럿 단위인 F 를 갖는 커패시턴스 값 C 를 제공한다는 것을 알고 있습니다 . 그러나 패럿은 그 자체로 매우 큰 단위이므로 사용하기에 실용적이지 않으므로 표준 패럿 단위의 약수 또는 분수가 대신 사용됩니다.
패럿이 실제로 얼마나 큰지에 대한 아이디어를 얻으려면 진공에서 작동하는 1mm의 합리적인 플레이트 간격으로 단 1패럿 값의 커패시터를 생성하는 데 필요한 플레이트의 표면적입니다. 위의 커패시턴스 방정식을 다시 정리하면 다음과 같은 플레이트 면적이 제공됩니다.
A = Cd ¼ 8.85pF/m = (1 x 0.001) ¼ 8.85×10 -12 = 112,994,350m 2
또는 1억 1,300만 m 2 이는 10km x 10km(6마일 이상) 정사각형 이상의 판과 동일합니다. 엄청나네요.1패럿 이상의 값을 갖는 커패시터는 고체 유전체를 갖는 경향이 있으며 "1패럿"은 사용하기에 매우 큰 단위이므로 마이크로패럿(μF ) , 나노 단위 로 제공되는 커패시터 값이 있는 전자 공식에서는 접두사가 대신 사용됩니다. -패럿( nF ) 및 피코패럿( pF ). 예를 들어:
패러드의 커패시턴스 하위 단위
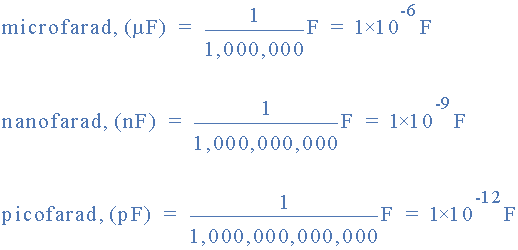
다음 정전 용량 값을 변환합니다.
a) 22nF~μF, b) 0.2μF~nF, c) 550pF~μF
a) 22nF = 0.022μF
b) 0.2μF = 200nF
다) 550pF = 0.00055μF
1패럿은 그 자체로 큰 값이지만, 이제 커패시터는 수백 패럿의 정전용량 값으로 일반적으로 사용 가능하며 이를 반영하는 "슈퍼 커패시터" 또는 "울트라 커패시터"라는 이름을 갖습니다.
이러한 커패시터는 탄소 유전체의 높은 표면적을 활용하여 기존 커패시터보다 훨씬 더 높은 에너지 밀도를 전달하는 전기화학적 에너지 저장 장치이며, 정전용량은 탄소 표면적에 비례하므로 탄소가 두꺼울수록 정전용량이 더 커집니다.
저전압(약 3.5V~5.5V) 슈퍼커패시터는 커패시터에 저장된 에너지가 1/2(C x V 2 ) 로 높은 정전용량 값으로 인해 많은 양의 전하를 저장할 수 있습니다 .
저전압 슈퍼 커패시터는 배터리와 같은 저장 및 방전 특성을 제공하여 대체 전원으로 사용하거나 메모리 백업에 이상적이기 때문에 크고 비싸며 무거운 리튬 유형 배터리를 대체하기 위해 휴대용 휴대용 장치에 일반적으로 사용됩니다. 휴대용 장치에 사용되는 슈퍼 커패시터는 일반적으로 장치에 장착된 태양 전지를 사용하여 충전됩니다.
울트라커패시터는 차량 오디오 및 비디오 시스템의 DC 평활 애플리케이션뿐만 아니라 대형 기존 배터리를 대체하기 위한 하이브리드 전기 자동차 및 대체 에너지 애플리케이션에 사용하기 위해 개발되고 있습니다. 울트라 커패시터는 신속하게 재충전할 수 있고 에너지 저장 밀도가 매우 높아 전기 자동차 애플리케이션에 사용하기에 이상적입니다.
커패시터의 에너지
커패시터가 연결된 전원 공급 장치에서 충전되면 커패시터에 에너지를 저장하는 정전기장이 형성됩니다. 이 정전기장에 저장된 줄 단위 의 에너지 양은 전압 공급 장치가 커패시터 플레이트의 전하를 유지하기 위해 가하는 에너지와 동일하며 다음 공식으로 제공됩니다.
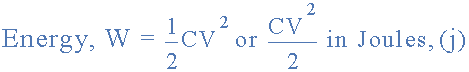
따라서 위의 100uF 커패시터 회로에 저장된 에너지는 다음과 같이 계산됩니다.
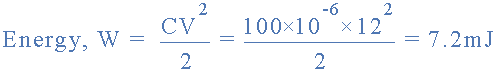
커패시터에 대한 섹션의 다음 튜토리얼에서는 커패시터 색상 코드를 살펴보고 커패시터의 커패시턴스와 전압 값이 본체에 표시되는 다양한 방식을 살펴봅니다.