
키르히호프 회로법
키르히호프의 회로 법칙을 사용하면 회로 주변의 전압과 전류에 대한 일련의 기본 네트워크 법칙과 정리를 정의하여 복잡한 회로 문제를 해결할 수 있습니다.
접합 규칙 및 폐루프 규칙과 관련된 키르히호프의 회로 법칙을 사용하여 폐회로 내의 전기 구성 요소 값을 알면 폐회로 주변의 전류와 전압을 계산하고 찾을 수 있습니다.
우리는 저항기 튜토리얼에서 두 개 이상의 저항기가 직렬, 병렬 또는 둘의 조합으로 함께 연결될 때 단일 등가 저항(RT)을 찾을 수 있으며 이러한 회로는 옴의 법칙을 따른다는 것을 확인했습니다 .
그러나 브리지나 T 네트워크와 같은 복잡한 회로에서는 옴의 법칙만으로는 회로 내에서 순환하는 전압이나 전류를 찾을 수 없는 경우가 있습니다. 이러한 유형의 계산을 위해서는 회로 방정식을 얻을 수 있는 특정 규칙이 필요하며 이를 위해 키르히호프의 회로 법칙을 사용할 수 있습니다 .
1845년 독일의 물리학자 구스타프 키르히호프(Gustav Kirchhoff) 는 전기 회로 내의 전류와 에너지 보존을 다루는 한 쌍 또는 일련의 규칙 또는 법칙을 개발했습니다. 이 두 가지 규칙은 일반적으로 다음과 같이 알려져 있습니다. 키르히호프 회로 법칙(Kirchhoffs Circuit Law )은 폐쇄 회로 주위에 흐르는 전류를 다루는 키르히호프 법칙 중 하나인 키르히호프 전류 법칙(KCL) 과 다른 법칙은 폐쇄 회로에 존재하는 전압 소스인 키르히호프 전압을 다룹니다. 법률, (KVL) .
Kirchhoff의 제1법칙 – 현행법(KCL)
키르히호프 전류법 (KCL)은 " 접합점이나 노드에 들어가는 총 전류 또는 전하는 노드 내에서 전하가 손실되지 않고 떠나는 것 외에는 갈 곳이 없기 때문에 노드를 떠나는 전하와 정확히 동일합니다 "라고 명시합니다. 즉, 노드에 들어오고 나가는 모든 전류의 대수적 합은 0, I (출구) + I (입력) = 0과 같아야 합니다. Kirchhoff의 이 아이디어는 일반적으로 전하 보존 으로 알려져 있습니다 .
키르히호프의 현행법
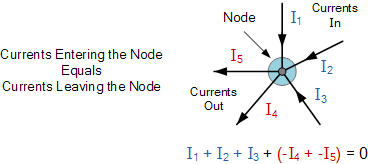
여기서 노드에 들어가는 세 전류 I 1 , I 2 , I 3 는 모두 값이 양수이고 노드에서 나가는 두 전류 I 4 및 I 5 는 값이 음수입니다. 그러면 이는 방정식을 다음과 같이 다시 작성할 수도 있음을 의미합니다.
나는 1 + 나는 2 + 나는 3 – 나는 4 – 나는 5 = 0
전기 회로에서 노드 라는 용어는 일반적으로 두 개 이상의 전류 전달 경로 또는 케이블 및 구성 요소와 같은 요소의 연결 또는 접합을 의미합니다. 또한 전류가 노드 안팎으로 흐르려면 폐쇄 회로 경로가 존재해야 합니다. 병렬 회로를 분석할 때 키르히호프의 전류법칙을 사용할 수 있습니다.
키르히호프의 제2법칙 - 전압 법칙(KVL)
키르히호프의 전압 법칙 (KVL)은 " 전압 소스에 의해 구동되는 모든 폐쇄 루프 네트워크에서 루프 주변의 총 전압은 동일한 루프 내의 모든 전압 강하의 합과 동일하다 "고 명시하며 이는 0과 같습니다. 즉, 폐루프 내의 모든 전압 소스와 전압 강하의 대수적 합은 0과 같아야 합니다. 왜냐하면 전압 강하의 대수적 합은 전압 소스의 대수적 합과 동일하기 때문입니다. Kirchhoff의 이 아이디어는 에너지 보존 으로 알려져 있습니다 .
키르히호프의 전압 법칙
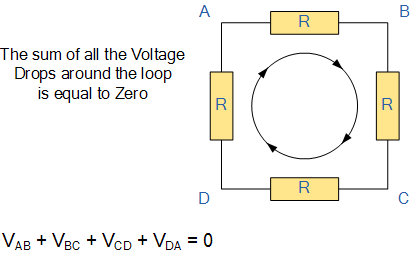
루프의 임의 지점에서 시작하여 동일한 방향 으로 계속 진행하여 모든 전압 강하 방향(양수 또는 음수)을 확인하고 동일한 시작점으로 돌아갑니다. 시계 방향이든 시계 반대 방향이든 동일한 방향을 유지하는 것이 중요합니다. 그렇지 않으면 최종 전압 합계가 0이 되지 않습니다. 직렬 회로를 분석할 때 키르히호프의 전압 법칙을 사용할 수 있습니다.
Kirchhoffs 회로 법칙을 사용하여 DC 회로 또는 AC 회로를 분석할 때 노드, 경로, 분기, 루프 및 메시와 같이 분석되는 회로 부분을 설명하기 위해 다양한 정의 및 용어가 사용됩니다. 이러한 용어는 회로 분석에서 자주 사용되므로 이해하는 것이 중요합니다.
공통 DC 회로 이론 용어:
- • 회로 – 회로는 전류가 흐르는 폐쇄 루프 전도 경로입니다.
- • 경로 – 요소나 소스를 연결하는 단일 선입니다.
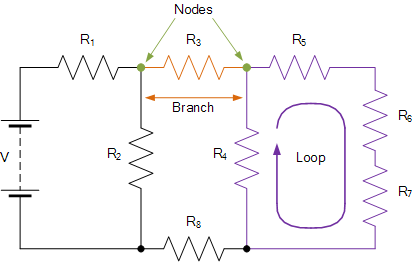
- • 노드 – 노드는 두 개 이상의 회로 요소가 연결되거나 함께 결합되어 두 개 이상의 가지 사이에 연결 지점을 제공하는 회로 내의 접합, 연결 또는 터미널입니다. 노드는 점으로 표시됩니다.
- • 분기 – 분기는 두 노드 사이에 연결된 저항기 또는 소스와 같은 단일 또는 구성 요소 그룹입니다.
- • 루프 – 루프는 회로 요소나 노드가 두 번 이상 발견되지 않는 회로의 단순한 닫힌 경로입니다.
- • 메쉬 – 메쉬는 다른 경로를 포함하지 않는 단일 폐쇄 루프 시리즈 경로입니다. 메시 내부에는 루프가 없습니다.
참고 사항:
모든 구성 요소에 동일한 전류 값이 흐를 경우 구성 요소는 직렬로 함께 연결되었다고 합니다.
구성 요소에 동일한 전압이 적용되면 구성 요소가 병렬로 함께 연결되었다고 합니다.
일반적인 DC 회로
키르히호프 회로법 예제 No1
40Ω 저항 R 3 에 흐르는 전류를 구합니다.
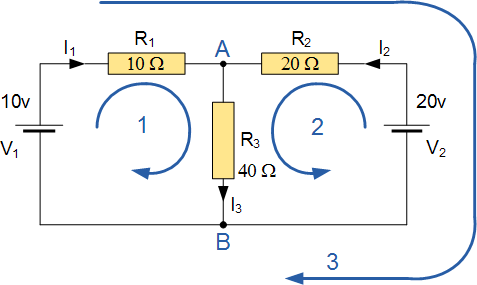
회로에는 3개의 분기, 2개의 노드( A 및 B ) 및 2개의 독립 루프가 있습니다.
Kirchhoff의 전류 법칙을 사용하여 KCL 방정식 은 다음과 같이 제공됩니다.
노드 A 에서 : I 1 + I 2 = I 3
노드 B 에서 : I 3 = I 1 + I 2
Kirchhoffs 전압 법칙을 사용하여 KVL 방정식 은 다음과 같이 제공됩니다.
루프 1은 다음과 같이 주어진다: 10 = R 1 I 1 + R 3 I 3 = 10I 1 + 40I 3
루프 2는 다음과 같이 주어진다: 20 = R 2 I 2 + R 3 I 3 = 20I 2 + 40I 3
루프 3은 다음과 같이 주어집니다: 10 – 20 = 10I 1 – 20I 2
I 3 은 I 1 + I 2 의 합이므로 방정식 을 다음과 같이 다시 작성할 수 있습니다.
방정식. 아니오 1 : 10 = 10I 1 + 40(I 1 + I 2 ) = 50I 1 + 40I 2
방정식. 아니오 2 : 20 = 20I 2 + 40(I 1 + I 2 ) = 40I 1 + 60I 2
이제 I 1 과 I 2 값을 제공하기 위해 빼기로 줄일 수 있는 두 개의 " 연립 방정식 "이 있습니다.
I 1 을 I 2 로 대체하면 I 1 의 값이 -0.143 암페어 로 제공됩니다.
I 1 을 I 2 로 대체하면 I 2 의 값이 +0.429 암페어 로 제공됩니다.
다음과 같이 : 나는 3 = 나는 1 + 나는 2
저항 R 3 에 흐르는 전류는 다음과 같이 주어진다: -0.143 + 0.429 = 0.286 Amps
저항기 R3 양단의 전압 은 다음과 같이 주어진다: 0.286 x 40 = 11.44V
I 1 의 음수 부호는 처음에 선택한 전류 흐름의 방향이 잘못되었지만 여전히 유효하다는 의미입니다. 실제로 20v 배터리는 10v 배터리를 충전하고 있습니다.
키르히호프 회로 법칙의 적용
이 두 법칙을 통해 회로의 전류 와 전압을 찾을 수 있습니다. 즉, 회로를 "분석"했다고 하며 키르히호프의 회로 법칙을 사용하는 기본 절차 는 다음과 같습니다.
- 1. 모든 전압과 저항이 주어진다고 가정합니다(그렇지 않은 경우 V1, V2,..R1, R2 등으로 라벨을 붙입니다).
- 2. 각 가지 또는 메시에 전류를 할당합니다(시계 방향 또는 시계 반대 방향).
- 3. 각 분기에 분기 전류를 표시합니다. ( I1, I2, I3 등)
- 4. 각 노드에 대한 키르히호프의 제1법칙 방정식을 찾습니다.
- 5. 회로의 각 독립 루프에 대한 키르히호프의 제2법칙 방정식을 찾으십시오.
- 6. 필요에 따라 선형 연립방정식을 사용하여 미지의 전류를 찾습니다.
키르히호프의 회로 법칙을 사용하여 선형 회로 주위를 순환하는 다양한 전압과 전류를 계산할 수 있을 뿐만 아니라 루프 분석을 사용하여 각 독립 루프의 전류를 계산할 수 있으므로 키르히호프의 법칙만 사용하여 필요한 수학의 양을 줄이는 데 도움이 됩니다. DC 회로에 대한 다음 튜토리얼에서는 이를 수행하기 위해 메시 전류 분석을 살펴보겠습니다.