메쉬 전류 분석
메시 전류 분석은 회로의 닫힌 경로에서 루프나 메시 주위를 순환하는 전류를 찾는 데 사용되는 기술입니다.
키르히호프의 법칙은 복잡한 전기 회로를 분석하기 위한 기본 방법을 제공하지만 메시 전류 분석 또는 노드 전압 분석을 사용하여 이 방법을 개선하는 다양한 방법이 있으므로 관련 수학을 줄이고 대규모 네트워크가 포함될 때 발생합니다. 수학의 이러한 감소는 큰 이점이 될 수 있습니다.
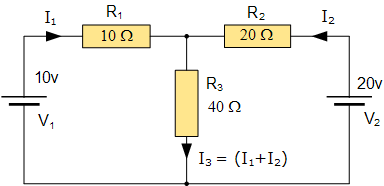
예를 들어, 이전 섹션의 전기 회로 예를 고려하십시오.
메시 전류 분석 회로
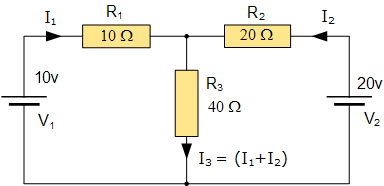
관련된 수학의 양을 줄이는 간단한 방법 중 하나는 Kirchhoff의 전류 법칙 방정식을 사용하여 회로를 분석하여 두 저항기에 흐르는 전류 I 1 및 I 2 를 결정하는 것입니다. 그러면 전류 I 3 을 I 1 과 I 2 의 합으로 계산할 필요가 없습니다 . 따라서 Kirchhoff의 두 번째 전압 법칙은 다음과 같습니다.
- 방정식 1: 10 = 50I 1 + 40I 2
- 방정식 2: 20 = 40I 1 + 60I 2
따라서 수학 계산의 한 줄이 저장되었습니다.
메쉬 전류 분석
위 회로를 해결하는 더 쉬운 방법은 메시 전류 분석(Mesh Current Analysis) 또는 루프 분석 (때때로 Maxwell의 순환 전류 방법이라고도 함)을 사용하는 것입니다. 분기 전류에 라벨을 붙이는 대신 순환 전류로 각 "폐쇄 루프"에 라벨을 붙일 필요가 있습니다.
일반적으로 순환 전류를 사용하여 시계 방향으로 내부 루프에만 레이블을 지정합니다. 목표는 회로의 모든 요소를 한 번 이상 덮는 것입니다. Kirchhoff 방법을 사용하기 전과 마찬가지로 적절한 루프 또는 메시 전류에서 필요한 분기 전류를 찾을 수 있습니다.
예: i 1 = I 1 , i 2 = -I 2 및 I 3 = I 1 – I 2
이제 키르히호프의 전압 법칙 방정식을 이전과 같은 방식으로 작성하여 문제를 해결하지만 이 방법의 장점은 회로 방정식에서 얻은 정보가 회로를 해결하는 데 필요한 최소한의 정보임을 보장한다는 것입니다. 쉽게 매트릭스 형태로 표현할 수 있습니다.
예를 들어, 이전 섹션의 회로를 고려해보세요.
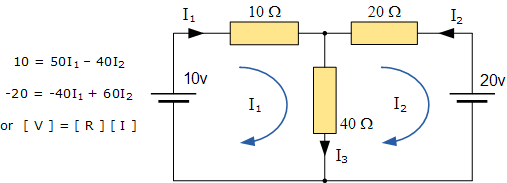
이러한 방정식은 단일 메시 임피던스 행렬 Z를 사용하여 매우 빠르게 풀 수 있습니다 . 주 대각선의 각 요소는 "양수"가 되며 각 메시의 총 임피던스입니다. 여기서 주대각선을 벗어난 각 요소는 "0" 또는 "음수"가 되며 모든 해당 메시를 연결하는 회로 요소를 나타냅니다.
먼저 우리는 행렬을 다룰 때 두 행렬을 나누는 것은 표시된 것처럼 한 행렬에 다른 행렬의 역을 곱하는 것과 같다는 것을 이해해야 합니다.
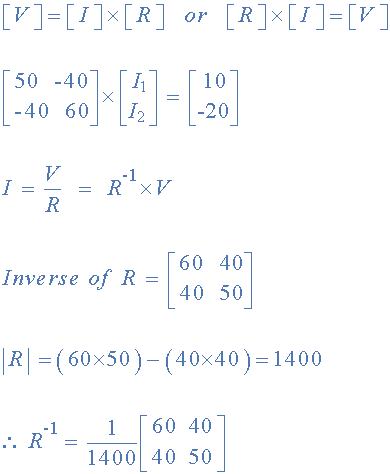
R 의 역수를 찾았 으므로 V/R은 V x R -1 과 동일하므로 이제 이를 사용하여 두 개의 순환 전류를 찾을 수 있습니다.
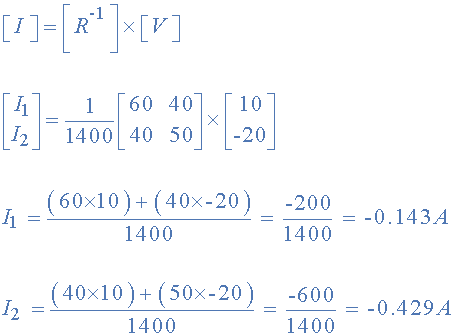
어디:
- [V]는 루프 1과 루프 2에 대한 총 배터리 전압을 제공합니다.
- [ I ]는 우리가 찾으려고 하는 루프 전류의 이름을 나타냅니다.
- [ R ]은 저항 매트릭스입니다.
- [ R -1 ]은 [ R ] 행렬의 역행렬입니다.
이는 I 1을 -0.143 Amps 로 , I 2를 -0.429 Amps 로 제공합니다.
다음과 같이: 나는 3 = 나는 1 – 나는 2
따라서 I 3 의 결합 전류는 -0.143 – (-0.429) = 0.286 Amps 로 제공됩니다.
이는 이전에 Kirchhoffs 회로 법칙 튜토리얼 에서 찾은 0.286A 전류 값과 동일합니다 .
튜토리얼 요약
회로 분석의 이 "보기" 방법은 아마도 메시 전류 분석 방정식을 풀기 위한 기본 절차가 다음과 같은 모든 회로 분석 방법 중에서 가장 좋을 것입니다.
- 1. 순환 전류로 모든 내부 루프에 라벨을 붙입니다. ( 나는 1 , 나는 2 , …나는 L 등)
- 2. 각 루프의 모든 전압 소스의 합을 제공하는 [ L x 1 ] 열 행렬 [ V ]를 작성합니다.
- 3. 회로의 모든 저항에 대한 [ L x L ] 행렬, [ R ]을 다음과 같이 작성합니다.
-
- R 11 = 첫 번째 루프의 총 저항.
- R nn = N번째 루프의 총 저항입니다.
- R JK = 루프 J를 루프 K에 직접 연결하는 저항입니다.
- 4. 행렬 또는 벡터 방정식 [V] = [R] x [I] 를 작성합니다. 여기서 [I] 는 찾을 전류 목록입니다.