부호 있는 이진수
부호 있는 이진수는 MSB를 부호 비트로 사용하여 양수 또는 음수의 범위를 표시합니다.
수학에서 양수(0 포함)는 부호 없는 숫자로 표시됩니다. 즉, 양수임을 표시하기 위해 앞에 +ve 기호를 넣지 않습니다. 그러나 음수를 처리할 때 숫자 앞에 -ve 기호를 사용하여 숫자가 음수 값이고 부호 없는 양수 값과 다르다는 것을 표시합니다. 부호 있는 이진수 에서도 마찬가지입니다 .
그러나 디지털 회로에서는 숫자에 더하기 또는 빼기 기호를 추가하는 규정이 없습니다. 왜냐하면 디지털 시스템은 "0"과 "1"로 표시되는 이진수로 작동하기 때문입니다. 마이크로 전자 공학에서 함께 사용되는 비트 ( BI nary digit T 의 축약형 )라고 불리는 이러한 “1”과 “0”은 바이트 또는 a 와 같은 일반적인 이름으로 참조되는 숫자의 여러 범위 크기에 속합니다. 단어 .
우리는 또한 이전에 8비트 이진수(1바이트)가 0(00000000 2 )에서 255(11111111 2 ) 범위의 값을 가질 수 있음을 확인했습니다. 즉, 단일 8비트를 구성하는 2 8 = 256개의 서로 다른 비트 조합 입니다. 바이트. 예를 들어 01001101 2 = 64 + 8 + 4 + 1 = 77 10 과 같은 부호 없는 이진수를 십진수로 표시합니다. 그러나 디지털 시스템과 컴퓨터는 양수뿐만 아니라 음수도 사용하고 조작할 수 있어야 합니다.
수학적인 숫자는 일반적으로 부호와 값(크기)으로 구성되는데, 부호는 숫자가 양수( + )인지 음수( - )인지를 나타내며, 값은 숫자의 크기를 나타냅니다. 예를 들어 23, + 156 또는 -274. 숫자를 표시하는 방식을 "부호-크기" 표현이라고 합니다. 가장 왼쪽 숫자는 부호를 나타내고 나머지 숫자는 숫자의 크기 또는 값을 나타내는 데 사용될 수 있기 때문입니다.
부호 크기 표기법은 0( 0 ) 양쪽의 양수와 음수를 나타내는 가장 간단하고 일반적인 방법 중 하나입니다 . 따라서 음수는 각 양수 또는 부호 없는 숫자가 예를 들어 +2와 -2, +10과 -10 등과 같이 부호 있는 반대 값을 갖기 때문에 해당 양수의 부호를 변경함으로써 간단히 얻을 수 있습니다.
하지만 우리가 가진 것이 1과 0의 묶음뿐이라면 어떻게 부호 있는 이진수를 표현할 수 있을까요? 우리는 이진수 또는 비트가 "1" 또는 "0"의 두 가지 값만 가지며 편리하게도 기호에도 " + " 또는 " - "의 두 가지 값만 있다는 것을 알고 있습니다.
그런 다음 단일 비트를 사용하여 부호 있는 이진수 의 부호를 값이 양수인지 음수인지 식별할 수 있습니다. 따라서 양의 이진수( +n )와 음의 이진수( -n )를 나타내려면 부호를 추가하여 사용할 수 있습니다.
부호 있는 이진수의 경우 최상위 비트(MSB)가 부호 비트로 사용됩니다. 부호 비트가 "0"이면 숫자 값이 양수임을 의미합니다. 부호 비트가 "1"이면 숫자 값은 음수입니다. 숫자의 나머지 비트는 일반적인 부호 없는 이진수 형식 방식으로 이진수의 크기를 나타내는 데 사용됩니다.
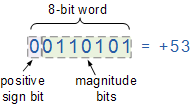
그런 다음 SM(Sign-and-Magnitude) 표기법이 "n" 총 비트를 두 부분으로 나누어 양수 및 음수 값을 저장한다는 것을 알 수 있습니다. 즉, 부호용 1비트와 순수 이진수 값용 n-1비트입니다. 숫자. 예를 들어, 10진수 53은 다음과 같이 8비트 부호 있는 이진수로 표현될 수 있다.
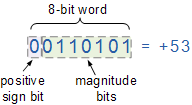
양수 부호 있는 이진수
음수 부호 있는 이진수
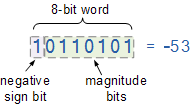
여기서 단점은 이전에는 전체 범위의 n비트 부호 없는 이진수를 사용했지만 이제는 다음과 같이 감소된 숫자 범위를 제공하는 n-1비트 부호 있는 이진수를 사용한다는 것입니다.
-2 (n-1) ~ +2 (n-1)
예를 들어 부호 있는 이진수를 나타내는 데 4비트가 있는 경우(부호 비트는 1비트 , 크기 비트 는 3비트 ), 부호-크기 표기법으로 표현할 수 있는 숫자의 실제 범위는 다음과 같습니다. :
-2 (4-1) – 1 ~ +2 (4-1) – 1
-2 (3) – 1 ~ +2 (3) – 1
-7 ~ +7
이전에는 부호 없는 4비트 이진수의 범위가 0 에서 15 , 16진수에서는 0 에서 F 였지만 이제는 범위가 -7에서 +7로 축소되었습니다. 따라서 부호 없는 이진수에는 단일 부호 비트가 없으므로 MSB(최상위 비트)가 사용된 부호 비트가 아닌 추가 비트 또는 숫자이므로 더 큰 이진 범위를 가질 수 있습니다.
부호-크기 형식의 또 다른 단점은 0, +0 또는 0000 2 에 대해 양수 결과를 얻을 수 있고 0, -0 또는 1000 2 에 대해 음수 결과를 얻을 수 있다는 것입니다 . 둘 다 유효하지만 어느 것이 정확합니까?
부호 있는 이진수 예제 No1
부호 크기 형식을 사용하여 다음 십진수 값을 부호 있는 이진수로 변환합니다.
| -15 6비트 숫자로 10 | ⇒ | 1011112 |
| 6비트 숫자로 +23 10 | ⇒ | 0101112 |
| -56 8비트 숫자로 10 | ⇒ | 101110002 |
| 8비트 숫자로 +85 10 | ⇒ | 010101012 |
| -127 8비트 숫자로 10 | ⇒ | 111111112 |
4비트, 6비트, 8비트, 16비트 또는 32비트 부호 있는 이진수의 경우 모든 비트에는 값이 있어야 합니다. 따라서 가장 왼쪽 부호 비트와 32비트 부호 비트 사이의 공간을 채우는 데 "0"이 사용됩니다. 첫 번째 또는 가장 높은 값 "1"입니다.
이진수의 부호 크기 표현은 부호 있는 이진수를 표현하기 위해 사용하고 이해하는 간단한 방법입니다. 수학에서 일반 십진수(기본 10) 숫자와 함께 이 시스템을 항상 사용하기 때문입니다. 이진수가 음수이면 앞에 "1"을 추가하고 양수이면 "0"을 추가합니다.
그러나 이 부호 크기 방법을 사용하면 동일한 이진 값을 갖는 두 개의 서로 다른 비트 패턴이 발생할 수 있습니다. 예를 들어 +0 과 -0은 부호 있는 4비트 이진수로 각각 0000 과 1000 이 됩니다 . 따라서 이 방법을 사용하면 0에 대한 두 가지 표현, 즉 양의 0( 0 000 2 )과 음의 0( 1 000 2 ) 이 있을 수 있으며 이는 컴퓨터와 디지털 시스템에 큰 문제를 일으킬 수 있습니다.
부호 있는 이진수의 보수
1의 보수 또는 1의 보수는 부호 있는 이진수 시스템에서 음의 이진수를 나타내는 데 사용할 수 있는 또 다른 방법입니다. 1의 보수에서 양수(비보수라고도 함)는 부호 크기 숫자와 마찬가지로 이전과 동일하게 유지됩니다.
그러나 음수는 부호 없는 양수의 1의 보수(역전, 부정)를 취하여 표현됩니다. 양수는 항상 "0"으로 시작하므로 보수는 음수를 나타내기 위해 항상 "1"로 시작합니다.
음수 이진수의 1의 보수는 양수에 대한 보수이므로, 이진수의 1의 보수를 취하려면 각 비트를 차례로 변경하기만 하면 됩니다. 따라서 "1"의 1의 보수는 "0"이고 그 반대의 경우 모든 1이 0으로, 0이 1로 변경되므로 10010100 2 의 1의 보수는 단순히 01101011 2 입니다.
디지털 산술 또는 논리 디코더 회로를 구축할 때 부호 있는 이진수의 1의 보수를 찾는 가장 쉬운 방법은 인버터를 사용하는 것입니다 . 인버터는 당연히 보수 생성기이며 병렬로 사용하여 표시된 대로 임의의 이진수의 1의 보수를 찾을 수 있습니다.
인버터를 사용한 1의 보수
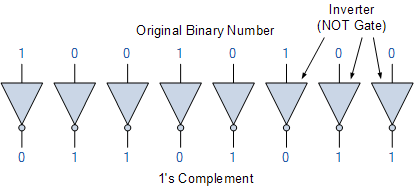
그런 다음 우리가 해야 할 일은 1을 0으로, 0을 1로 변경하여 -N 에 해당하는 값을 제공하기만 하면 이진수 N 의 1의 보수를 찾는 것이 매우 쉽다는 것을 알 수 있습니다 . 또한 이전 부호 크기 표현과 마찬가지로 1의 보수는 -2 (n-1) 및 +2 (n-1) – 1 범위의 숫자를 나타내는 n비트 표기법을 가질 수도 있습니다 . 예를 들어, 1의 보수 형식의 4비트 표현을 사용하여 이전과 동일하게 0의 두 가지 표현인 0000 (+0) 및 1111 (-0)을 사용하여 -7에서 +7까지 범위의 십진수를 표현할 수 있습니다. .
보수를 이용한 덧셈과 뺄셈
일의 보수 의 주요 장점 중 하나는 두 개의 이진수를 더하고 빼는 것입니다. 수학에서 뺄셈은 A – B 와 같이 다양한 방식으로 구현될 수 있으며 이는 A + (-B) 또는 -B + A 등 을 말하는 것과 같습니다 . 따라서 두 이진수를 뺄셈하는 복잡한 문제는 간단히 다음과 같이 수행할 수 있습니다. 추가를 사용합니다.
우리는 이진 가산기 튜토리얼에서 이진 덧셈이 이진수에 2개의 비트(숫자)만 있고 가장 큰 숫자가 "1"이라는 점을 제외하고 일반 덧셈과 동일한 규칙을 따른다는 것을 보았습니다. 십진수) 따라서 이진 덧셈에 가능한 조합은 다음과 같습니다.
| 0 | 0 | 1 | 1 | |
| + 0 | + 1 | + 0 | + 1 | |
| 0 | 1 | 1 | 1← 0 | (0 더하기 캐리 1) |
더할 두 숫자가 모두 양수(합 A + B) 인 경우 단일 비트를 더하면 "0 + 0"이 되기 때문에 직접 합(숫자와 비트 기호 포함)을 통해 두 숫자를 더할 수 있습니다. , "0 + 1" 또는 "1 + 0"의 합계는 "0" 또는 "1"이 됩니다. 그 이유는 우리가 더하고 싶은 두 비트가 홀수("0" + "1" 또는 "1 + 0")일 때 결과는 "1"이기 때문입니다. 마찬가지로 더할 두 비트가 짝수("0 + 0" 또는 "1 + 1")인 경우 "1 + 1"에 도달할 때까지 결과는 "0"입니다. 그런 다음 합계는 "0"에 a를 더한 것과 같습니다. "1"을 운반하십시오. 간단한 예를 살펴보겠습니다.
두 이진수의 빼기
1의 보수를 사용하여 다음 두 숫자 115와 27을 서로 빼려면 8비트 디지털 시스템이 필요합니다. 따라서 십진수로 계산하면 115 – 27 = 88 이 됩니다 .
먼저 두 개의 십진수를 이진수로 변환하고 앞에 0을 추가하여 8비트 숫자(바이트)를 생성하여 각 숫자의 비트 수가 동일한지 확인해야 합니다. 그러므로:
115 10 이진수는 다음과 같습니다: 01110011 2
27 10 이진수는 다음과 같습니다: 00011011 2
이제 첫 번째 숫자( 01110011 )는 변경하지 않고 두 번째 이진수( 00011011 ) 의 보수를 찾아야 합니다 . 따라서 모든 1을 0으로, 0을 1로 변경하면 00011011 의 1의 보수는 11100100 과 같습니다 .
첫 번째 숫자와 두 번째 숫자의 보수를 더하면 다음과 같습니다.
| 01110011 |
| + 11100100 |
| 오버플로 → 1 01010111 |
디지털 시스템은 8비트로 작동하므로 합계에 대한 답을 제공하는 데 처음 8자리만 사용되며 마지막 비트(비트 9)는 무시됩니다. 이 비트를 "오버플로" 비트라고 합니다. 오버플로는 가장 중요한(가장 왼쪽) 열의 합이 이월을 생성할 때 발생합니다. 이 오버플로 또는 캐리 비트는 완전히 무시되거나 계산에 사용하기 위해 다음 디지털 섹션으로 전달될 수 있습니다. 오버플로는 대답이 긍정적임을 나타냅니다. 오버플로가 없으면 대답은 부정적입니다.
위의 8비트 결과는 다음과 같습니다: 01010111 (오버플로 “1”이 취소됨) 이를 1의 보수 답에서 실제 답으로 다시 변환하려면 이제 1의 보수 결과에 “1”을 추가해야 합니다. 따라서 다음과 같습니다.
| 01010111 |
| + 1 |
| 01011000 |
따라서 이진수에서 1의 보수를 사용하여 115( 01110011 2 )에서 27( 00011011 2 ) 을 뺀 결과는 10 진수로 01011000 2 또는 (64 + 16 + 8) = 88 10 이 됩니다 .
그러면 부호 있는 이진수와 부호 없는 이진수를 1의 보수 와 덧셈 과정을 통해 서로 뺄 수 있음을 알 수 있습니다 . TTL 74LS83 또는 74LS283과 같은 이진 가산기는 두 개의 4비트 부호 있는 이진수를 더하거나 빼는 데 사용되거나 함께 계단식으로 연결되어 캐리아웃이 완료된 8비트 가산기를 생성할 수 있습니다.
2의 보수
2의 보수 또는 2의 보수는 이전의 부호 크기 및 1의 보수 형식과 같은 또 다른 방법으로, 부호 있는 이진수 시스템에서 음의 이진수를 나타내는 데 사용할 수 있습니다. 2의 보수에서 양수는 부호 없는 이진수의 이전과 정확히 동일합니다. 그러나 음수는 이진수로 표시되며, 해당 양수에 해당하는 값을 더하면 0이 됩니다.
2의 보수 형식에서 음수는 기본적으로 이전과 거의 동일한 프로세스를 사용하여 두 숫자를 빼는 A – B = A + (B의 2의 보수) 인 양수의 2의 보수입니다 . 2의 보수는 1의 보수입니다. + 1.
이전 보수에 비해 2의 보수의 주요 장점은 이중 0 문제가 없으며 부호 있는 이진수의 2의 보수를 생성하는 것이 훨씬 더 쉽다는 것입니다. 따라서 숫자가 2의 보수 형식으로 표현될 때 산술 연산을 수행하기가 상대적으로 더 쉽습니다.
위에서 2의 보수를 사용하여 두 개의 8비트 숫자 115와 27을 빼는 방법을 살펴보겠습니다. 위에서 이진수는 다음과 같습니다.
115 10 이진수는 다음과 같습니다: 01110011 2
27 10 이진수는 다음과 같습니다: 00011011 2
숫자의 길이는 8비트이고 값을 나타내는 데 사용할 수 있는 28 자리 숫자가 있으며 이진수로는 100000000 2 또는 256 10과 같습니다 . 그러면 27 10 의 2의 보수는 다음 과 같습니다:
(28)2 – 00011011 = 100000000 – 00011011 = 111001012
두 번째 음수의 보수는 뺄셈이 두 숫자의 더하기가 훨씬 쉬워진다는 것을 의미하므로 합계는 다음과 같습니다. 115 + (27의 2의 보수) 이는 다음과 같습니다.
01110011 + 11100101 = 1 010110002
이전과 마찬가지로 첫 번째 8비트에만 관심이 있으므로 9번째 오버플로 비트는 무시됩니다. 따라서 결과는 이전과 동일하게 십진수로 01011000 2 또는 (64 + 16 + 8) = 88 10 입니다.
튜토리얼 요약
우리는 MSB(최상위 비트)를 부호 비트로 사용하여 음의 이진수를 표현할 수 있다는 것을 살펴보았습니다. n 비트 이진수가 부호 있는 경우 가장 왼쪽 비트는 부호를 나타내는 데 사용되며 n-1 비트는 숫자를 나타냅니다.
예를 들어, 4비트 이진수에서는 실제 숫자를 보유하는 데 3비트만 남습니다. 그러나 이진수에 부호가 없으면 모든 비트를 사용하여 숫자를 나타낼 수 있습니다.
부호 있는 이진수의 표현은 일반적으로 부호 크기 표기법 이라고 하며 부호 비트가 "0"이면 숫자는 양수입니다. 부호 비트가 "1"이면 숫자는 음수입니다. 이진 산술 연산을 처리할 때는 음수의 보수를 사용하는 것이 더 편리합니다.
보수는 음의 이진수를 표현하는 또 다른 방법입니다. 이 대체 코딩 시스템을 사용하면 간단한 덧셈을 사용하여 음수를 뺄 수 있습니다.
양의 부호 크기 숫자는 항상 0으로 시작하므로 보수는 다음 표에 표시된 것처럼 음수를 나타내기 위해 항상 1로 시작합니다.
4비트 부호 있는 이진수 비교
| 소수 | 부호 있는 크기 | 서명된 보수 | 부호 있는 2의 보수 |
| +7 | 0111 | 0111 | 0111 |
| +6 | 0110 | 0110 | 0110 |
| +5 | 0101 | 0101 | 0101 |
| +4 | 0100 | 0100 | 0100 |
| +3 | 0011 | 0011 | 0011 |
| +2 | 0010 | 0010 | 0010 |
| +1 | 0001 | 0001 | 0001 |
| +0 | 0000 | 0000 | 0000 |
| -0 | 1000 | 1111 | – |
| -1 | 1001 | 1110 | 1111 |
| -2 | 1010 | 1101 | 1110 |
| -3 | 1011 | 1100 | 1101 |
| -4 | 1100 | 1011 | 1100 |
| -5 | 1101 | 1010 | 1011 |
| -6 | 1110 | 1001 | 1010 |
| -7 | 1111 | 1000 | 1001 |
부호 있는 보수 형식의 이진수는 1의 보수 또는 2의 보수를 사용할 수 있습니다. 이진수의 1의 보수와 2의 보수는 음수의 표현을 허용하기 때문에 중요합니다.
2의 보수 산술 방법은 음수를 처리하기 위해 컴퓨터에서 일반적으로 사용됩니다. 유일한 단점은 부호 있는 이진수 형식으로 음의 이진수를 표현하려면 이전에 사용했던 양수의 범위 중 일부를 포기해야 한다는 것입니다. .
'전자일기' 카테고리의 다른 글
| 논리 AND 기능 (0) | 2024.01.26 |
|---|---|
| 이진수 튜토리얼 (0) | 2024.01.26 |
| 이진수에서 십진수로의 변환 (0) | 2024.01.23 |
| 이진수 (0) | 2024.01.17 |
| 패시브 감쇠기 튜토리얼 (1) | 2024.01.15 |