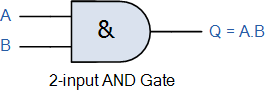
논리 AND 기능
논리 AND 함수 출력은 모든 입력이 참인 경우에만 참이고, 그렇지 않으면 출력은 거짓입니다.
부울 대수학은 논리 AND 함수와 같은 각 부울 함수가 일반적으로 하나 이상의 입력 값을 가지며 이러한 입력 값을 기반으로 출력 결과를 생성하는 논리 함수를 기반으로 합니다. 입력에는 0 또는 1의 두 가지 값 중 하나가 있습니다.
1854년에 조지 불(George Boole)은 "군" 또는 "집합" 이론의 단순화된 버전을 기반으로 한 "사고의 법칙"에 대한 조사를 수행했으며 이로부터 부울 대수학이 개발되었습니다. 부울 대수학은 논리와 집합 연산이 둘 다 "TRUE" 또는 "FALSE"이지만 동시에 둘 다는 아니라는 이론을 주로 다룹니다.
예를 들어, A + A = A 이고 일반 대수학에서는 2A 가 아닙니다. 부울 대수는 표준 논리 게이트의 전환 동작을 나타내는 간단하고 효과적인 방법이며 여기서 우리와 관련된 기본 논리 문은 AND , OR 및 NOT 게이트 기능의 논리 게이트 연산으로 제공됩니다.
논리 AND 함수
논리 AND 기능 기능은 두 개 이상의 이벤트가 동시에 발생해야 출력 동작이 발생함을 나타냅니다. 이러한 작업이 수행되는 순서는 최종 결과에 영향을 주지 않으므로 중요하지 않습니다. 예를 들어 A & B = B & A 입니다 . 부울 대수에서 논리 AND 함수는 두 변수의 위치 변경을 허용하는 교환 법칙을 따릅니다.
AND 기능은 점 또는 마침표 기호( . )로 전자적으로 표시됩니다. 따라서 2입력( AB ) AND 게이트에는 부울 표현식 A 로 표시 되는 출력 항이 있습니다 . B 또는 그냥 AB .
AND 기능의 스위치 표현
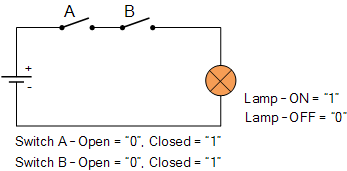
여기에서는 두 개의 스위치 A 와 B가 함께 연결되어 직렬 회로를 형성합니다. 따라서 위의 회로에서 램프를 켜려면 스위치 A 와 스위치 B 가 모두 닫혀야 합니다(논리 "1"). 즉, 램프가 "ON"이 되려면 두 스위치가 모두 닫혀 있거나 논리 "1"에 있어야 합니다.
그런 다음 이 유형의 논리 게이트( AND 게이트)는 "모든" 입력이 존재할 때만 출력을 생성합니다. 부울 대수학 용어 로 말하면 모든 입력이 TRUE인 경우에만 출력 이 TRUE 가 됩니다 . 전기적 측면에서 논리 AND 기능은 위에 표시된 직렬 회로와 동일합니다.
스위치는 2개뿐이므로 각 스위치는 "열림" 또는 "닫힘"의 두 가지 상태를 가질 수 있습니다. 스위치가 열려 있을 때 논리 "0"을 정의하고 스위치가 닫혀 있을 때 논리 "1"을 정의하면 그림과 같이 두 스위치를 함께 배열하는 네 가지 방법 또는 조합이 있습니다.
AND 함수 진리표
| 스위치 A | 스위치 B | 산출 | 설명 |
| 0 | 0 | 0 | A, B 모두 개방, 램프 꺼짐 |
| 0 | 1 | 0 | A는 열림, B는 닫힘, 램프 꺼짐 |
| 1 | 0 | 0 | A가 닫히고 B가 열림, 램프 꺼짐 |
| 1 | 1 | 1 | A가 닫히고 B가 닫혀 램프 ON |
| 부울 표현식(A AND B) | ㅏ . 비 | ||
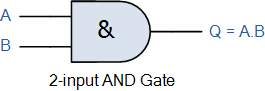
논리 AND 게이트는 일반 TTL 74LS08 4중 2입력 포지티브 AND 게이트(또는 4081 CMOS 동급) TTL 74LS11 3중 3입력 포지티브 AND 게이트 또는 74LS21 듀얼 4입력 포지티브 AND 게이트와 같은 표준 IC 패키지로 제공됩니다. . AND 게이트를 함께 "계단식" 연결하여 입력이 4개 이상인 회로를 생성할 수도 있습니다.
'전자일기' 카테고리의 다른 글
| 부울 대수학의 법칙 (0) | 2024.01.28 |
|---|---|
| 논리 NOR 기능 (0) | 2024.01.28 |
| 로직 NAND 기능 (1) | 2024.01.26 |
| 논리 NOT 기능 (0) | 2024.01.26 |
| 논리 OR 기능 (1) | 2024.01.26 |