혼합 주파수 신호에 관한 장에서 우리는 AC 시스템의 고조파 개념 , 즉 기본 소스 주파수의 정수 배수인 주파수에 대해 알아보았습니다.
교류 발전기에서 나오는 소스 전압 파형이 왜곡되지 않은 단일 주파수 사인파여야 하는 교류 전원 시스템 의 경우 이상적으로는 고조파 성분이 없어야 합니다.
AC 시스템의 비선형 구성 요소
비선형 구성 요소가 없다면 이는 사실일 것입니다 . 비선형 구성 요소는 소스 전압에 비해 불균형하게 전류를 끌어와 비정현파 전류 파형을 발생시킵니다.
비선형 부품의 예로는 가스 방전 램프, 반도체 전력 제어 장치( 다이오드 , 트랜지스터 , SCR, TRIAC), 변압기 (1차 권선 자화 전류는 일반적으로 코어의 B/H 포화 곡선으로 인해 비사인파임) 및 전기 모터(모터 코어 내의 자기장이 포화 수준 근처에서 작동하는 경우)가 있습니다.
백열전구도 온도가 빠르게 변하면 필라멘트 저항이 사이클 내내 변하기 때문에 약간 비정현파 전류를 생성합니다.
혼합 주파수 장에서 배웠듯이, 사인파 모양의 파형이 왜곡되면 고조파 주파수가 발생합니다 .
문제의 비사인파가 평균 중심선 위아래로 대칭인 경우, 고조파 주파수는 기본 소스 주파수의 홀수 정수 배수만 되고 짝수 정수 배수는 없습니다.
대부분의 비선형 부하는 이와 같은 전류 파형을 생성하므로 대부분의 AC 전원 시스템에서는 짝수 번째 고조파(2차, 4차, 6차, 8차, 10차, 12차 등)가 없거나 최소한으로만 존재합니다.
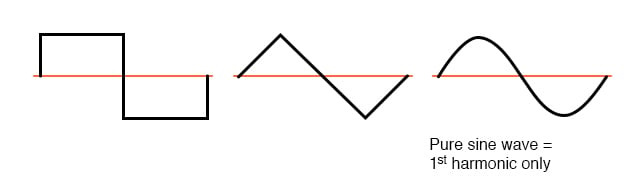
대칭 파형의 예 - 홀수 고조파만 해당.
아래 그림에서는 짝수 고조파가 존재하는 비대칭 파형의 예를 참고로 보여줍니다.
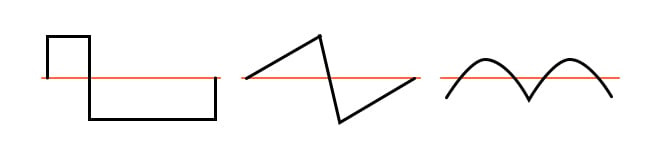
비대칭 파형의 예 - 균일한 고조파가 존재합니다.
가능한 고조파 주파수의 절반이 비선형 부하의 전형적으로 대칭적인 왜곡에 의해 제거되더라도, 홀수 고조파는 여전히 문제를 일으킬 수 있습니다. 이러한 문제 중 일부는 단상이든 아니든 모든 전력 시스템에 일반적입니다.
예를 들어, 와전류 손실로 인한 변압기 과열은 상당한 고조파 성분이 있는 모든 AC 전원 시스템에서 발생할 수 있습니다.
그러나 다상 전력 시스템에서만 나타나는 고조파 전류로 인한 몇 가지 문제가 있으며, 이 섹션에서는 바로 이러한 문제에 대해 구체적으로 설명합니다.
고조파 효과에 관한 SPICE 시뮬레이션
SPICE에서 비선형 하중을 시뮬레이션할 수 있으면 복잡한 수학을 피하고 고조파 효과를 보다 직관적으로 이해하는 데 도움이 됩니다.
선형 AC 시스템 시뮬레이션
먼저, 우리는 매우 간단한 AC 회로로 시뮬레이션을 시작할 것입니다. 순수 선형 부하와 모든 관련 저항을 갖는 단일 사인파 전압 소스입니다.
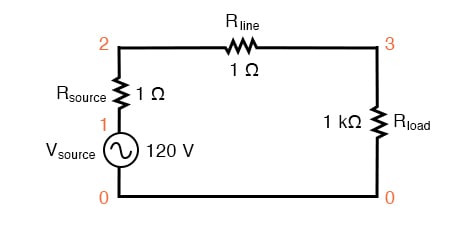
단일 사인파 소스를 갖춘 SPICE 회로.
이 회로의 R 소스 저항 과 R 라인 저항은 실제 세계를 모방하는 것 이상의 역할을 합니다. 이 저항은 SPICE 시뮬레이션 에서 전류를 측정하기 위한 편리한 션트 저항을 제공하기도 합니다 . 1Ω 저항의 전압을 읽으면 E = IR이므로 전류를 직접 알 수 있습니다.
이 회로의 SPICE 시뮬레이션(SPICE 목록: "선형 부하 시뮬레이션")과 R 라인 에서 측정된 전압에 대한 푸리에 분석은 이 회로의 라인 전류의 고조파 함량을 보여줍니다. 본질적으로 완전히 선형적이므로 60Hz 소스를 가정할 때 60Hz의 1차(기본) 외에는 고조파가 없을 것으로 예상됩니다.
SPICE 출력 “과도 응답 v(2,3)의 푸리에 구성 요소”와 아래 그림을 참조하세요.
선형 하중 시뮬레이션
vsource 1 0 sin(0 120 60 0 0)
소스 1 2 1
r라인 2 3 1
rload 3 0 1k
.옵션 itl5=0
.트랜 0.5m 30m 0 1u
.플롯 전환 v(2,3)
.4 60 v(2,3)
.끝
과도 응답의 푸리에 성분 v(2,3)
직류성분 = 4.028E-12
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 5.793E-12 0.000000 51.122 123.122
3 1.800E+02 7.407E-12 0.000000 -34.624 37.376
4 2.400E+02 9.056E-12 0.000000 4.267 76.267
5 3.000E+02 1.651E-11 0.000000 -83.461 -11.461
6 3.600E+02 3.931E-11 0.000000 36.399 108.399
7 4.200E+02 2.338E-11 0.000000 -41.343 30.657
8 4.800E+02 4.716E-11 0.000000 53.324 125.324
9 5.400E+02 3.453E-11 0.000000 21.691 93.691
총 고조파 왜곡 = 0.000000 퍼센트

단일 주파수 성분의 주파수 영역 플롯. SPICE 목록 참조: "선형 부하 시뮬레이션".
.plot 명령은 SPICE 넷리스트에 나타나고, 일반적으로 이것은 사인파 그래프 출력을 초래합니다. 그러나 이 경우 간결함을 위해 의도적으로 파형 표시를 생략했습니다. .plot 명령은 SPICE의 푸리에 변환 함수의 기이한 점을 충족하기 위해 넷리스트에 있습니다.
완벽한 이산 푸리에 변환은 없으므로 모든 주파수에 대해 9번째 고조파(표 참조)까지 매우 작은 고조파 전류(피코 암페어 범위!)가 표시됩니다. 이는 SPICE가 푸리에 분석을 수행하는 데 있어 그 한계입니다.
1차 고조파 또는 기본 주파수의 "푸리에 성분"에 대해 0.1198 암페어(1.198E-01)를 표시하는데, 이는 예상 부하 전류로, 소스 전압이 120볼트이고 부하 저항이 1kΩ일 때 약 120mA입니다.
단순 비선형 단상 AC 시스템 시뮬레이션
다음으로, 고조파 전류를 생성하기 위해 비선형 부하를 시뮬레이션하고 싶습니다. 이는 근본적으로 두 가지 다른 방법으로 수행할 수 있습니다. 한 가지 방법은 SPICE로 시뮬레이션하기 쉬운 다이오드나 다른 반도체 장치와 같은 비선형 구성 요소를 사용하여 부하를 설계하는 것입니다. 다른 방법은 부하 저항과 병렬로 일부 AC 전류 소스를 추가하는 것입니다.
후자의 방법은 엔지니어가 고조파를 시뮬레이션하는 데 선호하는 경우가 많습니다 . 알려진 값의 전류원은 매우 복잡한 응답 특성을 지닌 구성 요소보다 수학적 네트워크 분석에 더 적합하기 때문입니다.
SPICE가 모든 수학 작업을 하게 되므로 반도체 부품의 복잡성은 우리에게 아무런 문제가 되지 않지만, 전류원은 임의의 양의 전류를 생성하도록 미세 조정될 수 있으므로(편리한 기능) 아래 그림과 SPICE 목록인 "비선형 부하 시뮬레이션"에 표시된 후자의 접근 방식을 선택하겠습니다.
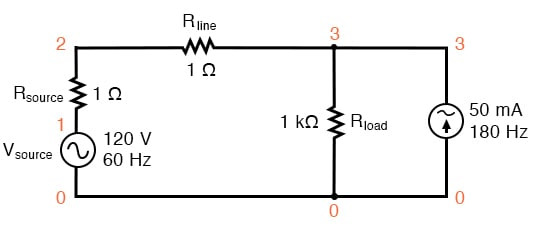
SPICE 회로: 3차 고조파가 추가된 60Hz 소스.
비선형 하중 시뮬레이션 vsource 1 0 sin(0 120 60 0 0)
소스 1 2 1
r라인 2 3 1
rload 3 0 1k
이3하르 3 0 신(0 50m 180 0 0)
.옵션 itl5=0
.트랜 0.5m 30m 0 1u
.플롯 전환 v(2,3)
.4 60 v(2,3)
.끝
이 회로에서 우리는 50 mA 크기의 전류원과 180 Hz의 주파수를 가지고 있는데, 이는 60 Hz의 소스 주파수의 3배입니다. 1 kΩ 부하 저항과 병렬로 연결하면, 그 전류는 저항의 전류와 더해져 비정현파 총 라인 전류를 만듭니다.
아래 그림에서 파형 플롯을 보여드리면 3차 고조파 전류가 전체 전류에 미치는 영향을 보실 수 있습니다. 전체 전류는 일반적으로 단순 사인파입니다.
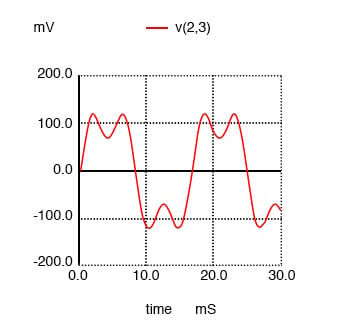
60Hz 소스와 180Hz의 3차 고조파의 합을 보여주는 SPICE 시간 영역 플롯입니다.
과도 응답의 푸리에 성분 v(2,3)
직류성분 = 1.349E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 1.609E-11 0.000000 67.570 139.570
3 1.800E+02 4.990E-02 0.416667 144.000 216.000
4 2.400E+02 1.074E-10 0.000000 -169.546 -97.546
5 3.000E+02 3.871E-11 0.000000 169.582 241.582
6 3.600E+02 5.736E-11 0.000000 140.845 212.845
7 4.200E+02 8.407E-11 0.000000 177.071 249.071
8 4.800E+02 1.329E-10 0.000000 156.772 228.772
9 5.400E+02 2.619E-10 0.000000 160.498 232.498
총 고조파 왜곡률 = 41.666663퍼센트
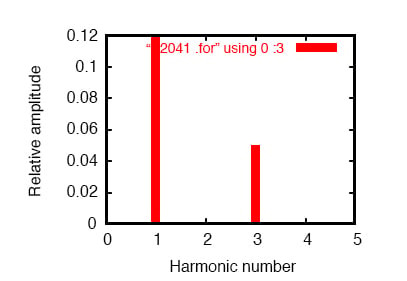
60Hz 소스와 180Hz의 3차 고조파를 보여주는 SPICE 푸리에 플롯입니다.
푸리에 분석에서는 (위의 그림과 “과도 응답의 푸리에 성분 v(2,3)” 참조) 혼합 주파수는 혼합되지 않고 별도로 표시됩니다.
여기서 우리는 첫 번째 시뮬레이션에서와 같은 60Hz(기본) 전류의 0.1198 암페어를 보지만, 3번째 고조파 행에 49.9mA가 나타납니다. 우리의 50mA, 180Hz 전류 소스가 작동합니다. 왜 선을 통해 50mA 전체를 보지 못할까요?
그 전류원은 1kΩ 부하 저항기에 연결되어 있기 때문에, 일부 전류는 부하를 통해 분류되고 결코 라인을 통해 소스로 돌아가지 않습니다. 부하의 한 부분이 "정상"(저항기)이고 다른 부분이 전류원에 의해 모방되는 이런 유형의 시뮬레이션의 불가피한 결과입니다.
다중 전류 소스를 사용한 비선형 단상 AC 시스템 시뮬레이션
"부하"에 더 많은 전류 소스를 추가한다면 이상적인 사인파 모양에서 선 전류 파형이 더욱 왜곡되는 것을 볼 수 있으며, 이러한 고조파 전류는 각각 푸리에 분석 고장에 나타납니다. 아래 그림과 SPICE 목록인 "비선형 부하 시뮬레이션"을 참조하세요.
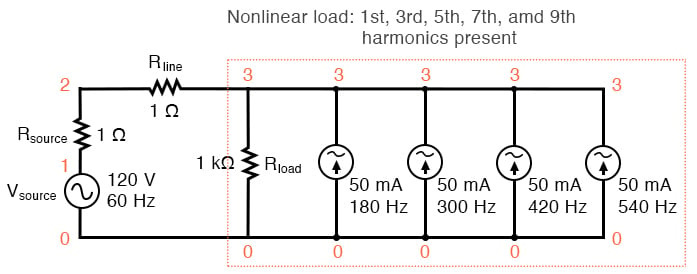
비선형 부하: 1차, 3차, 5차, 7차, 9차 고조파가 존재합니다.
비선형 하중 시뮬레이션
vsource 1 0 sin(0 120 60 0 0)
소스 1 2 1
r라인 2 3 1
rload 3 0 1k
이3하르 3 0 신(0 50m 180 0 0)
i5har 3 0 sin(0 50m 300 0 0)
이7하르 3 0 신(0 50m 420 0 0)
이9하르 3 0 신(0 50m 540 0 0)
.옵션 itl5=0
.트랜 0.5m 30m 0 1u
.플롯 전환 v(2,3)
.4 60 v(2,3) .끝
과도 응답의 푸리에 성분 v(2,3)
직류성분 = 6.299E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 -72.000 0.000
2 1.200E+02 1.900E-09 0.000000 -93.908 -21.908
3 1.800E+02 4.990E-02 0.416667 144.000 216.000
4 2.400E+02 5.469E-09 0.000000 -116.873 -44.873
5 3.000E+02 4.990E-02 0.416667 0.000 72.000
6 3.600E+02 6.271E-09 0.000000 85.062 157.062
7 4.200E+02 4.990E-02 0.416666 -144.000 -72.000
8 4.800E+02 2.742E-09 0.000000 -38.781 33.219
9 5.400E+02 4.990E-02 0.416666 72.000 144.000
총 고조파 왜곡률 = 83.333296퍼센트

푸리에 분석: “과도 응답의 푸리에 구성 요소 v(2,3)”.
푸리에 분석(위의 그림)에서 볼 수 있듯이 모든 고조파 전류원은 각각 49.9mA로 선 전류에 동등하게 표현됩니다. 지금까지는 단상 전력 시스템 시뮬레이션일 뿐입니다.
3상 AC 시스템 시뮬레이션
3상 시뮬레이션으로 만들면 더욱 흥미로운 일이 일어납니다. 두 개의 푸리에 분석이 수행됩니다. 하나는 라인 저항기 전압에 대한 것이고, 다른 하나는 중성 저항기 전압에 대한 것입니다.
이전과 마찬가지로, 각각 1Ω의 고정 저항을 가로지르는 전압을 읽으면 해당 저항을 통과하는 전류를 직접 알 수 있습니다. 아래 그림과 SPICE 목록 "고조파가 있는 YY 소스/부하 4선 시스템"을 참조하세요.
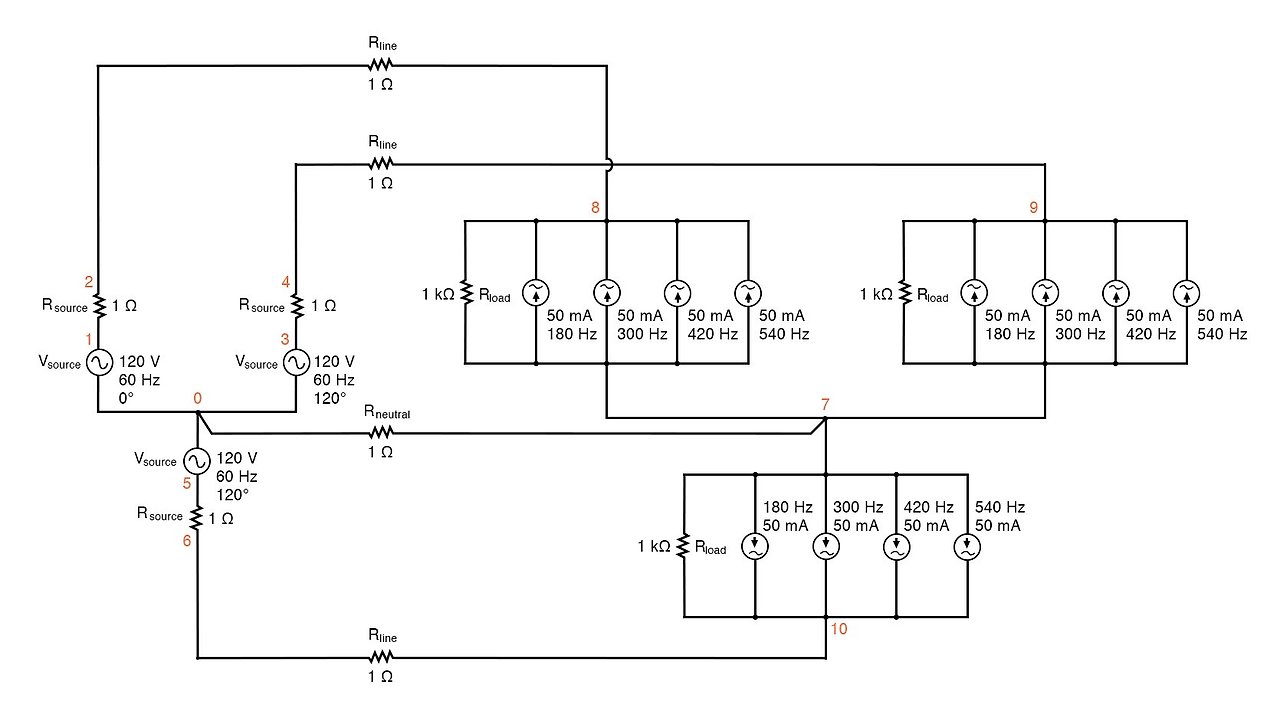
SPICE 회로: "라인 전류" 및 "중성 전류" 분석, 고조파를 포함한 YY 소스/부하 4선 시스템.
고조파를 포함한 YY 소스/부하 4선 시스템
*
* phase1 전압원과 r(120v/_ 0도)
vsource1 1 0 죄(0 120 60 0 0)
rsource1 1 2 1
*
* phase2 전압원과 r(120v/_ 120도)
vsource2 3 0 죄(0 120 60 5.55555m 0)
소스2 3 4 1
*
* phase3 전압원과 r(120v/_ 240도)
vsource3 5 0 죄(0 120 60 11.1111m 0)
rsource3 5 6 1
*
* 라인 및 중성선 저항
rline1 2 8 1
r라인2 4 9 1
r라인3 6 10 1
중립 0 7 1
*
* 로드의 1단계
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 0 0)
i5har1 8 7 sin(0 50m 300 0 0)
i7har1 8 7 죄(0 50m 420 0 0)
i9har1 8 7 sin(0 50m 540 0 0)
*
* 로드의 2단계
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 5.55555m 0)
i5har2 9 7 죄(0 50m 300 5.55555m 0)
i7har2 9 7 죄(0 50m 420 5.55555m 0)
i9har2 9 7 죄(0 50m 540 5.55555m 0)
*
* 로드의 3단계
rload3 10 7 1k
i3har3 10 7 sin(0 50m 180 11.1111m 0)
i5har3 10 7 sin(0 50m 300 11.1111m 0)
i7har3 10 7 sin(0 50m 420 11.1111m 0)
i9har3 10 7 sin(0 50m 540 11.1111m 0)
*
* 분석 자료
.옵션 itl5=0
.트랜 0.5m 100m 12m 1u
.플롯 전환 v(2,8)
.4 60 v(2,8)
.플롯 전환 v(0,7)
.4 60 v(0,7)
.끝
선 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(2,8)
직류성분 = -6.404E-12
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 0.000 0.000
2 1.200E+02 2.218E-10 0.000000 172.985 172.985
3 1.800E+02 4.975E-02 0.415423 0.000 0.000
4 2.400E+02 4.236E-10 0.000000 166.990 166.990
5 3.000E+02 4.990E-02 0.416667 0.000 0.000
6 3.600E+02 1.877E-10 0.000000 -147.146 -147.146
7 4.200E+02 4.990E-02 0.416666 0.000 0.000
8 4.800E+02 2.784E-10 0.000000 -148.811 -148.811
9 5.400E+02 4.975E-02 0.415422 0.000 0.000
총 고조파 왜곡률 = 83.209009퍼센트
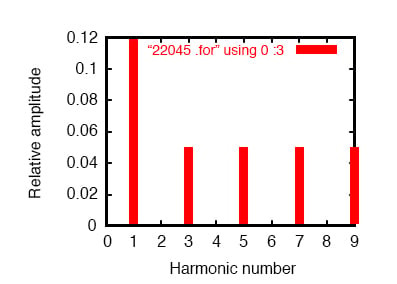
평형 YY 시스템의 선전류에 대한 푸리에 분석.
중성 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(0,7)
직류성분 = 1.819E-10
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 4.337E-07 1.000000 60.018 0.000
2 1.200E+02 1.869E-10 0.000431 91.206 31.188
3 1.800E+02 1.493E-01 344147.7638 -180.000 -240.018
4 2.400E+02 1.257E-09 0.002898 -21.103 -81.121
5 3.000E+02 9.023E-07 2.080596 119.981 59.963
6 3.600E+02 3.396E-10 0.000783 15.882 -44.136
7 4.200E+02 1.264E-06 2.913955 59.993 -0.025
8 4.800E+02 5.975E-10 0.001378 35.584 -24.434
9 5.400E+02 1.493E-01 344147.4889 -179.999 -240.017
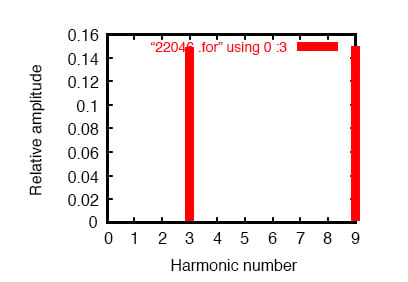
중성 전류의 푸리에 분석은 고조파가 없다는 것 외에는 아무것도 보여주지 않습니다! 위 그림의 선 전류와 비교해보세요.
이것은 균형 잡힌 YY 전력 시스템으로, 각 위상은 앞서 시뮬레이션한 단상 AC 시스템과 동일합니다. 따라서 3상 시스템의 한 위상에서 라인 전류에 대한 푸리에 분석이 단상 시스템의 라인 전류에 대한 푸리에 분석과 거의 동일하다는 것은 놀라운 일이 아닙니다. 기본(60Hz) 라인 전류는 0.1198 암페어이고 홀수 고조파 전류는 각각 약 50mA입니다.
위의 그림과 푸리에 분석을 참조하세요: “과도 응답의 푸리에 구성 요소 v(2,8)”
여기서 놀라운 점은 SPICE 노드 0과 7 사이의 R 중성 저항기 에서 전압 강하에 의해 결정되는 중성선 전류에 대한 분석입니다 .
균형 잡힌 3상 Y 부하에서 중성 전류는 0일 것으로 예상합니다. 각 상 전류는 중성선을 거쳐 소스 Y의 공급 상으로 돌아가는데, 모두 크기가 같고 모두 120° 떨어져 있기 때문에 중성 도체와 관련하여 서로 상쇄되어야 합니다.
고조파 전류가 없는 시스템에서는 이런 일 이 발생하여 중성선을 통과하는 전류는 전혀 흐르지 않습니다.
시스템의 고조파 전류의 영향
하지만 동일한 시스템 내의 고조파 전류 에 대해서는 똑같은 말을 할 수 없습니다 .
기본 주파수(60Hz 또는 1차 고조파) 전류는 중성선에서 사실상 존재하지 않는다는 점에 유의하십시오. 우리의 푸리에 분석은 R neutral 에 걸리는 전압을 읽을 때 1차 고조파의 0.4337µA만 보여줍니다 . 5차 및 7차 고조파에 대해서도 마찬가지라고 할 수 있는데, 두 전류 모두 무시할 수 있는 크기를 갖습니다.
대조적으로, 3차 및 9차 고조파는 중성선 내에서 강하게 표현되며, 각각 149.3mA(1Ω에서 1.493E-01볼트)입니다! 이는 각각 150mA에 매우 가깝거나 전류원 값의 3배입니다.
부하에 고조파 주파수당 3개의 소스가 있는 경우 각 위상의 3차 및 9차 고조파 전류가 합쳐져 중성 전류를 형성하는 것으로 보입니다. 푸리에 분석 참조: "과도 응답의 푸리에 구성 요소 v(0,7)"
시간 영역 그래프 분석
이것이 바로 일어나고 있는 일이지만, 왜 그런지는 분명하지 않을 수도 있습니다.
이를 이해하는 열쇠는 위상 전류의 시간 영역 그래프에서 명확하게 드러납니다. 위상 시퀀스가 1-2-3인 시간에 따른 균형 위상 전류의 이 플롯을 살펴보세요. (아래 그림)
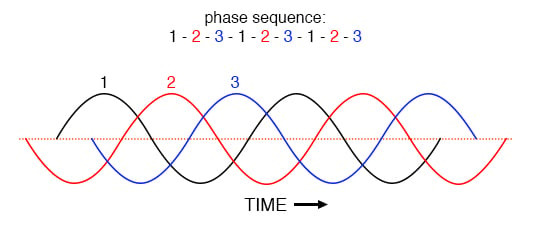
균일하게 간격이 있는 파동의 위상 순서는 1-2-3-1-2-3-1-2-3입니다.
그래프의 시간 축을 따라 3개의 기본 파형이 동일하게 이동하면 중성 도체에서 결과 전류가 0이 되도록 서로 상쇄되는 방식을 쉽게 알 수 있습니다. 하지만 아래 그림의 그래프에 중첩된 위상 1의 3차 고조파 파형이 어떻게 보일지 생각해 보겠습니다.

3상 기본 파형에 중첩된 1상 3차 고조파 파형입니다.
이 고조파 파형이 1차와 마찬가지로 2차 및 3차 기본 파형과 동일한 위상 관계를 가지고 있는 방식을 살펴보세요. 모든 기본 파형의 양의 반주기마다 고조파 파형의 양의 반주기가 정확히 2개, 음의 반주기가 1개 있습니다.
이것이 의미하는 바는 3개의 120° 위상 편이 기본 주파수 파형의 3차 고조파 파형이 실제로 서로 동상이라는 것입니다 . 일반적으로 3상 AC 시스템에서 가정하는 120° 위상 편이 수치는 기본 주파수에만 적용되며 고조파 배수에는 적용되지 않습니다!
세 개의 3차 고조파 파형을 모두 같은 그래프에 표시하면 정확히 겹쳐지고 단일의 통합된 파형으로 나타납니다(아래 그림에서 굵은 글씨로 표시).
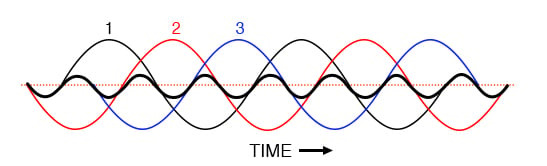
1, 2, 3상의 3차 고조파는 기본 3상 파형에 중첩되면 모두 일치합니다.
시간 영역 그래프의 수학적 분석
수학에 더 관심이 있는 사람들을 위해 이 원리는 상징적으로 표현될 수 있습니다. A 가 하나의 파형을 나타내고 B가 다른 파형을 나타낸다고 가정해 보겠습니다. 둘 다 같은 주파수이지만 위상 면에서 서로 120° 이동했습니다. 각 파형의 3차 고조파를 각각 A' 및 B' 라고 합시다 .
A' 와 B' 사이의 위상 변화는 120°(즉 A 와 B 사이의 위상 변화 )가 아니라 3배입니다. A' 와 B' 파형은 A 와 B 보다 3배 빠르게 번갈아가기 때문입니다. 파형 사이의 변화는 동일한 각속도가 가정될 때만 위상 각도 로 정확하게 표현됩니다 .
다른 주파수의 파형을 연관시킬 때 위상 변화를 표현하는 가장 정확한 방법은 시간 으로 표현하는 것입니다 . 그리고 A' 와 B' 사이의 시간 변화는 3배 낮은 주파수에서 120° 또는 A' 와 B' 의 주파수에서 360°와 같습니다 . 360°의 위상 변화는 0°의 위상 변화와 같으며, 즉 위상 변화가 전혀 없다는 것을 의미합니다.
따라서 A' 와 B' 는 서로 동상이어야 합니다.

3상 시스템의 3차 고조파의 이러한 특성은 3차 고조파의 정수 배수에도 그대로 적용됩니다.
따라서 각 기본 파형의 3차 고조파 파형이 서로 동상일 뿐만 아니라, 6차 고조파, 9차 고조파, 12차 고조파, 15차 고조파, 18차 고조파, 21차 고조파 등도 동상입니다.
파형 왜곡이 중심선에 대해 대칭인 시스템에서는 홀수 고조파만 나타나고 대부분의 비선형 부하는 대칭 왜곡을 생성하므로 3차 고조파의 짝수 배수(6차, 12차, 18차 등)는 일반적으로 중요하지 않고 홀수 배수(3차, 9차, 15차, 21차 등)만이 중성 전류에 크게 기여합니다.
3개가 아닌 다른 여러 위상이 있는 다상 전력 시스템에서 이 효과는 동일한 배수의 고조파에서 발생합니다. 예를 들어, 기본 파형 간의 위상 편이가 90°인 별 연결 4상 시스템의 중성 도체를 추가하는 고조파 전류는 4번째, 8번째, 12번째, 16번째, 20번째 등이 됩니다.
트리플렌 하모닉스
3상 전력 시스템에서 풍부하고 중요한 역할을 하기 때문에 3차 고조파와 그 배수는 고유한 이름인 ' 삼중 고조파'를 갖습니다 .
모든 삼중 고조파는 4선 Y 연결 부하의 중성 도체에서 서로 더해집니다. 상당한 비선형 부하를 포함하는 전력 시스템에서 삼중 고조파 전류는 중성 도체가 과열될 만큼 충분히 클 수 있습니다.
이것은 매우 문제가 됩니다. 왜냐하면 다른 안전 문제로 인해 중성선에 과전류 보호 기능을 적용할 수 없기 때문에 이러한 높은 전류를 자동으로 차단할 방법이 없기 때문입니다.
YY 회로에서 삼중 고조파의 효과 분석
다음 그림은 부하에서 생성된 삼중 고조파 전류가 중성선 내에서 어떻게 더해지는지 보여줍니다. 기호 "ω"는 각속도를 나타내는 데 사용되며 수학적으로 2πf와 동일합니다. 따라서 "ω"는 기본 주파수를 나타내고 "3ω"는 3차 고조파를 나타내고 "5ω"는 5차 고조파를 나타냅니다. (아래 그림)
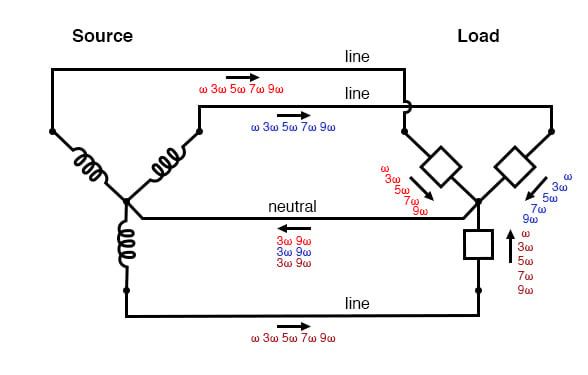
“YY” 3중 소스/부하: 고조파 전류가 중성선에 추가됩니다.
이러한 가산적 삼중 전류를 완화하기 위해 중성선을 완전히 제거하고 싶을 수도 있습니다. 삼중 전류가 함께 흐를 수 있는 중성선이 없다면, 그렇지 않겠습니까?
불행히도 그렇게 하면 다른 문제가 발생합니다. 부하의 "Y" 중심점이 더 이상 소스와 동일한 전위에 있지 않게 되며, 이는 부하의 각 위상이 소스에서 생성된 것과 다른 전압을 수신한다는 것을 의미합니다.
1 Ω R 중성 저항 없이 마지막 SPICE 시뮬레이션을 다시 실행하여 무슨 일이 일어나는지 살펴보겠습니다.
고조파를 포함한 YY 소스/부하(중성선 없음)
*
* phase1 전압원과 r(120v/0도)
vsource1 1 0 죄(0 120 60 0 0)
rsource1 1 2 1
*
* phase2 전압원과 r(120v/120도)
vsource2 3 0 죄(0 120 60 5.55555m 0)
소스2 3 4 1
*
* phase3 전압원과 r(120v/240도)
vsource3 5 0 죄(0 120 60 11.1111m 0)
rsource3 5 6 1
*
* 라인 저항
rline1 2 8 1
r라인2 4 9 1
r라인3 6 10 1
*
* 로드의 1단계
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 0 0)
i5har1 8 7 sin(0 50m 300 0 0)
i7har1 8 7 죄(0 50m 420 0 0)
i9har1 8 7 sin(0 50m 540 0 0)
*
* 로드의 2단계
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 5.55555m 0)
i5har2 9 7 죄(0 50m 300 5.55555m 0)
i7har2 9 7 죄(0 50m 420 5.55555m 0)
i9har2 9 7 죄(0 50m 540 5.55555m 0)
*
* 로드의 3단계
rload3 10 7 1k
i3har3 10 7 sin(0 50m 180 11.1111m 0)
i5har3 10 7 sin(0 50m 300 11.1111m 0)
i7har3 10 7 sin(0 50m 420 11.1111m 0)
i9har3 10 7 sin(0 50m 540 11.1111m 0)
*
* 분석 자료
.옵션 itl5=0
.트랜 0.5m 100m 12m 1u
.플롯 전환 v(2,8)
.4 60 v(2,8)
.플롯 전환 v(0,7)
.4 60 v(0,7)
.플롯 전환 v(8,7)
.4 60 v(8,7)
.끝
선 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(2,8)
직류성분 = 5.423E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 0.000 0.000
2 1.200E+02 2.388E-10 0.000000 158.016 158.016
3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009
4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510
5 3.000E+02 4.990E-02 0.416665 0.000 0.000
6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565
7 4.200E+02 4.990E-02 0.416668 0.000 0.000
8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638
9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005
총 고조파 왜곡률 = 58.925539퍼센트
두 "Y" 중심점 사이의 전압에 대한 푸리에 분석:
과도 응답의 푸리에 성분 v(0,7)
직류성분 = 6.093E-08
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.453E-04 1.000000 60.018 0.000
2 1.200E+02 6.263E-08 0.000431 91.206 31.188
3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018
4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121
5 3.000E+02 3.023E-04 2.080596 119.981 59.963
6 3.600E+02 1.138E-07 0.000783 15.882 -44.136
7 4.200E+02 4.234E-04 2.913955 59.993 -0.025
8 4.800E+02 2.001E-07 0.001378 35.584 -24.434
9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017
총 고조파 왜곡 = ************ 퍼센트
부하 위상 전압의 푸리에 분석:
과도 응답의 푸리에 구성 요소 v(8,7)
직류성분 = 6.070E-08
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E+02 1.000000 0.000 0.000
2 1.200E+02 6.231E-08 0.000000 90.473 90.473
3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000
4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747
5 3.000E+02 9.995E-02 0.000835 179.850 179.850
6 3.600E+02 1.023E-07 0.000000 13.485 13.485
7 4.200E+02 9.959E-02 0.000832 179.790 179.789
8 4.800E+02 1.991E-07 0.000000 35.462 35.462
9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999
총 고조파 왜곡률 = 59.043467퍼센트
정말 이상한 일들이 일어나고 있네요.
첫째, 우리는 삼중 고조파 전류(3차 및 9차)가 부하를 소스에 연결하는 라인에서 거의 사라진다는 것을 봅니다. 5차 및 7차 고조파 전류는 정상 수준(약 50mA)으로 존재하지만 3차 및 9차 고조파 전류는 무시할 수 있는 크기입니다.
두 번째로, 우리는 두 개의 "Y" 중심점 사이에 상당한 고조파 전압이 있음을 알 수 있습니다. 이 두 지점 사이에는 중성선이 연결되었습니다. SPICE에 따르면, 이 두 지점 사이에는 3차 및 9차 고조파 주파수가 모두 50볼트 있는데, 이는 선형(고조파 없음) 균형 Y 시스템에서는 분명히 정상이 아닙니다.
마지막으로, 부하의 한 위상(SPICE 분석에서 노드 8과 7 사이)에서 측정된 전압 역시 각각 50볼트의 강한 3중 고조파 전압을 보여줍니다.
아래 그림은 앞서 언급한 효과를 그래픽으로 요약한 것입니다.
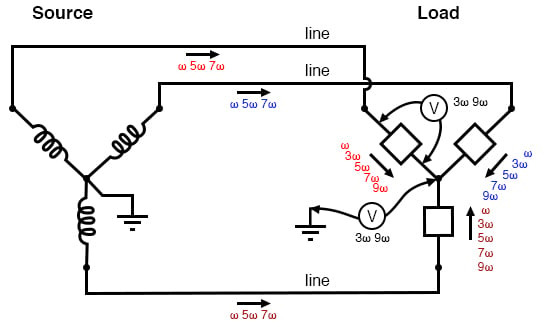
3선 "YY"(중립 없음) 시스템: "Y" 센터 사이에 3배 전압이 나타납니다. 부하 위상에 3배 전압이 나타납니다. 라인 도체에 3배가 아닌 전류가 나타납니다.
요약하자면, 중성선을 제거하면 부하 "Y"에 "뜨거운" 중심점이 생기고, 모두 3배 주파수로 구성된 동일한 크기의 고조파 부하 위상 전압이 발생합니다.
이전 시뮬레이션에서는 4선식 Y결선 시스템에서 고조파로 인한 바람직하지 않은 영향은 과도한 중성 전류 였지만 적어도 부하의 각 위상은 고조파가 거의 없는 전압을 수신했습니다.
델타-와이(Y) 회로에서의 삼중 고조파 효과 분석
중성선을 제거해도 고조파로 인한 문제를 제거하는 데 효과가 없는 듯하므로, 아마도 Δ 구성으로 전환하면 효과가 있을 것입니다. Y 대신 Δ 소스를 시도해 보고 부하를 현재 Y 구성으로 유지한 다음 무슨 일이 일어나는지 살펴보겠습니다.
측정된 매개변수는 라인 전류(R 라인 , 노드 0 및 8의 전압), 부하 위상 전압(노드 8 및 7), 소스 위상 전류(R 소스 , 노드 1 및 2의 전압) 입니다 . (아래 그림)

고조파를 포함한 Delta-Y 소스/부하
고조파를 포함한 Delta-Y 소스/부하
*
* phase1 전압원과 r(120v/_ 0도)
vsource1 1 0 죄(0 207.846 60 0 0)
rsource1 1 2 1
*
* phase2 전압원과 r(120v/_ 120도)
vsource2 3 2 죄(0 207.846 60 5.55555m 0)
소스2 3 4 1
*
* phase3 전압원과 r(120v/_ 240도)
vsource3 5 4 죄(0 207.846 60 11.1111m 0)
rsource3 5 0 1
*
* 라인 저항
rline1 0 8 1
r라인2 2 9 1
r라인3 4 10 1
*
* 로드의 1단계
rload1 8 7 1k
i3har1 8 7 sin(0 50m 180 9.72222m 0)
i5har1 8 7 sin(0 50m 300 9.72222m 0)
i7har1 8 7 sin(0 50m 420 9.72222m 0)
i9har1 8 7 sin(0 50m 540 9.72222m 0)
*
* 로드의 2단계
rload2 9 7 1k
i3har2 9 7 sin(0 50m 180 15.2777m 0)
i5har2 9 7 sin(0 50m 300 15.2777m 0)
i7har2 9 7 죄(0 50m 420 15.2777m 0)
i9har2 9 7 죄(0 50m 540 15.2777m 0)
*
* 로드의 3단계
rload3 10 7 1k
i3har3 10 7 죄(0 50m 180 4.16666m 0)
i5har3 10 7 죄(0 50m 300 4.16666m 0)
i7har3 10 7 죄(0 50m 420 4.16666m 0)
i9har3 10 7 죄(0 50m 540 4.16666m 0)
*
* 분석 자료
.옵션 itl5=0
.트랜 0.5m 100m 16m 1u
.plot 트랜 v(0,8) v(8,7) v(1,2)
.4 60 v(0,8) v(8,7) v(1,2)
.끝
참고: 다음 문단은 내 SPICE 넷리스트의 모든 세부 사항을 따르는 호기심 많은 독자를 위한 것입니다. 회로에서 무슨 일이 일어나는지 알고 싶다면 이 문단을 건너뛰세요!
주파수와 위상이 다른 AC 소스를 갖는 회로를 시뮬레이션할 때 SPICE에서 이를 수행하는 유일한 방법은 지연 시간 또는 위상 오프셋을 초 단위로 지정하여 소스를 설정하는 것입니다. 따라서 0° 소스에는 다음과 같은 5가지 지정 수치가 있습니다. “(0 207.846 60 0 0)”는 0볼트 DC 오프셋, 207.846볼트 피크 진폭(3의 제곱근을 120배하여 부하 위상 전압이 각각 120볼트로 유지되도록 함), 60Hz, 0 시간 지연 및 0 감쇠 계수를 의미합니다.
120° 위상이 이동된 소스는 다음과 같은 수치를 갖습니다: “(0 207.846 60 5.55555m 0)”, 모두 첫 번째 수치와 동일하지만 시간 지연 계수가 5.55555밀리초, 즉 60Hz 파형의 전체 주기인 16.6667밀리초의 1/3입니다.
240° 소스는 해당 양의 두 배인 240/360의 16.6667밀리초 또는 11.1111밀리초만큼 시간 지연이 있어야 합니다.
이는 Δ-연결 소스에 대한 것입니다. 반면 Y-연결 부하는 고조파 전류 소스에 대해 다른 시간 지연 수치 집합이 필요합니다. Y 부하의 위상 전압이 Δ 소스의 위상 전압과 동상이 아니기 때문입니다.
Δ 소스 전압 VAC, VBA 및 VCB가 각각 0°, 120° 및 240°로 참조되는 경우 "Y" 부하 전압 VA, VB 및 VC는 각각 -30°, 90° 및 210°의 위상각을 갖게 됩니다.
이것은 모든 Δ-Y 회로의 본질적인 속성이며 SPICE의 특이점이 아닙니다. 따라서 고조파 소스의 지연 시간을 지정할 때 15.2777밀리초(-30° 또는 +330°), 4.16666밀리초(90°), 9.72222밀리초(210°)로 설정해야 했습니다.
마지막으로 SPICE에서 AC 소스를 지연시킬 때 지연 시간이 경과할 때까지 "켜지지" 않습니다. 즉, 그 시점까지의 모든 수학적 분석은 오류가 발생합니다. 따라서 .tran 과도 분석 라인을 설정하여 시작 후 16밀리초가 될 때까지 분석을 보류하도록 했습니다. 이렇게 하면 넷리스트의 모든 소스가 분석이 수행되기 전에 작동할 시간을 얻을 수 있습니다.
이 분석의 결과는 마지막 분석만큼이나 실망스럽습니다. (아래 그림) 선 전류는 변함없습니다(유일한 실질적인 고조파 함량은 5차와 7차 고조파임). 부하 위상 전압도 변함없으며, 각 부하 구성 요소에 3배 고조파(3차와 9차) 주파수가 50볼트입니다.
소스 위상 전류는 라인 전류의 일부에 불과하며, 이는 놀랄 일이 아닙니다. 5차와 7차 고조파가 모두 표현되며, 무시할 수 있는 3배 고조파가 있습니다.
선 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(0,8)
직류성분 = -6.850E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E-01 1.000000 150.000 0.000
2 1.200E+02 2.491E-11 0.000000 159.723 9.722
3 1.800E+02 1.506E-06 0.000013 0.005 -149.996
4 2.400E+02 2.033E-11 0.000000 52.772 -97.228
5 3.000E+02 4.994E-02 0.416682 30.002 -119.998
6 3.600E+02 1.234E-11 0.000000 57.802 -92.198
7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998
8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200
9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995
총 고조파 왜곡률 = 58.925038퍼센트
부하 위상 전압의 푸리에 분석:
과도 응답의 푸리에 구성 요소 v(8,7)
직류성분 = 1.259E-08
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.198E+02 1.000000 150.000 0.000
2 1.200E+02 1.941E-07 0.000000 49.693 -100.307
3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998
4 2.400E+02 1.519E-07 0.000000 66.397 -83.603
5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112
6 3.600E+02 2.433E-07 0.000000 68.162 -81.838
7 4.200E+02 6.931E-02 0.000578 148.548 -1.453
8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897
9 5.400E+02 5.000E+01 0.417221 90.006 -59.995
총 고조파 왜곡률 = 59.004109퍼센트
소스 위상 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(1,2)
직류성분 = 3.564E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 6.906E-02 1.000000 -0.181 0.000
2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493
3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815
4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390
5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815
6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745
7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813
8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694
9 5.400E+02 4.267E-06 0.000062 0.006 0.186
총 고조파 왜곡률 = 59.031969퍼센트
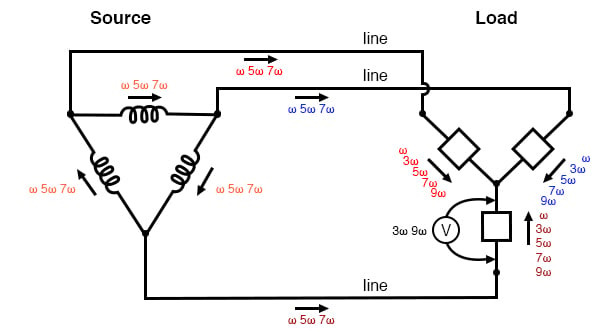
"Δ-Y" 소스/부하: 부하 위상에 걸쳐 삼중 전압이 나타납니다. 비삼중 전류는 라인 도체와 소스 위상 권선에 나타납니다.
실제로, 고조파 관점에서 Δ-Y 구성의 유일한 장점은 더 이상 부하에 충격 위험을 초래하는 중심점이 없다는 것입니다. 그렇지 않으면 부하 구성 요소는 동일한 고조파가 풍부한 전압을 받고 선은 3선 Y 시스템에서와 동일한 전류를 봅니다.
델타-델타 회로에서 삼중 고조파의 효과 분석
시스템을 Δ-Δ 배열로 재구성한다면(아래 그림 참조) 각 부하 위상이 각 소스 위상과 병렬로 직접 연결되므로 각 부하 구성 요소가 비고조파 전압을 수신하는 것이 보장됩니다.
Δ-Δ 시스템에는 중성선이나 "중심점"이 전혀 없기 때문에 이상한 전압이나 가산 전류가 발생하는 것을 방지할 수 있습니다.
이상적인 해결책인 듯합니다. 시뮬레이션하고 관찰하여 선 전류, 부하 위상 전압, 소스 위상 전류를 분석해 보겠습니다. SPICE 목록을 참조하세요: "고조파가 있는 델타-델타 소스/부하", "푸리에 분석: 과도 응답 v(0,6)의 푸리에 구성 요소", "과도 응답 v(2,1)의 푸리에 구성 요소".
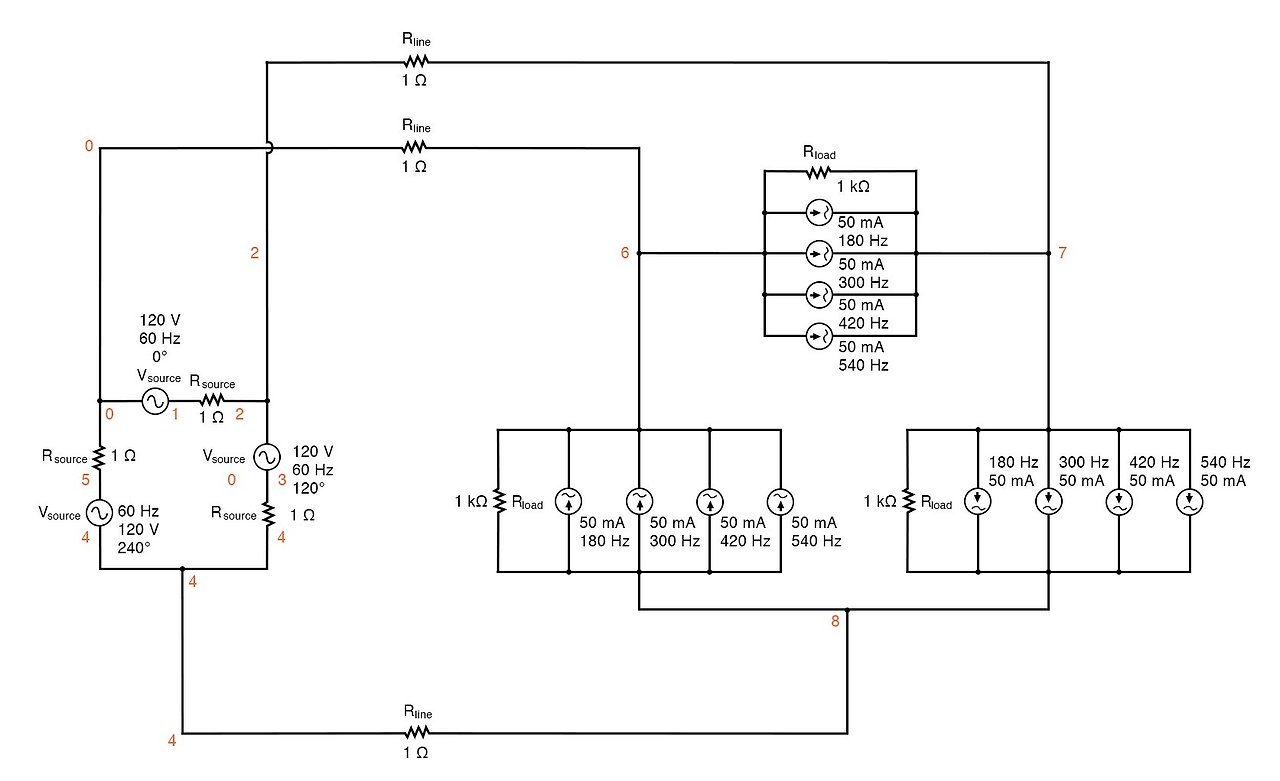
고조파를 포함한 델타-델타 소스/부하.
고조파를 포함한 델타-델타 소스/부하
*
* phase1 전압원과 r(120v/_ 0도)
vsource1 1 0 죄(0 120 60 0 0)
rsource1 1 2 1
*
* phase2 전압원과 r(120v/_ 120도)
vsource2 3 2 죄(0 120 60 5.55555m 0)
소스2 3 4 1
*
* phase3 전압원과 r(120v/_ 240도)
vsource3 5 4 죄(0 120 60 11.1111m 0)
rsource3 5 0 1
*
* 라인 저항
rline1 0 6 1
r라인2 2 7 1
r라인3 4 8 1
*
* 로드의 1단계
rload1 7 6 1k
i3har1 7 6 sin(0 50m 180 0 0)
i5har1 7 6 sin(0 50m 300 0 0)
i7har1 7 6 죄(0 50m 420 0 0)
i9har1 7 6 sin(0 50m 540 0 0)
*
* 로드의 2단계
rload2 8 7 1k
i3har2 8 7 sin(0 50m 180 5.55555m 0)
i5har2 8 7 죄(0 50m 300 5.55555m 0)
i7har2 8 7 죄(0 50m 420 5.55555m 0)
i9har2 8 7 죄(0 50m 540 5.55555m 0)
*
* 로드의 3단계
rload3 6 8 1k
i3har3 6 8 sin(0 50m 180 11.1111m 0)
i5har3 6 8 sin(0 50m 300 11.1111m 0)
i7har3 6 8 sin(0 50m 420 11.1111m 0)
i9har3 6 8 sin(0 50m 540 11.1111m 0)
*
* 분석 자료
.옵션 itl5=0
.트랜 0.5m 100m 16m 1u
.plot tran v(0,6) v(7,6) v(2,1) i(3har1)
.4 60 v(0,6) v(7,6) v(2,1)
.끝
선 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(0,6)
직류성분 = -6.007E-11
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 2.070E-01 1.000000 150.000 0.000
2 1.200E+02 5.480E-11 0.000000 156.666 6.666
3 1.800E+02 6.257E-07 0.000003 89.990 -60.010
4 2.400E+02 4.911E-11 0.000000 8.187 -141.813
5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000
6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997
7 4.200E+02 8.626E-02 0.416669 150.001 0.001
8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940
9 5.400E+02 1.877E-06 0.000009 89.987 -60.013
총 고조파 왜곡률 = 58.925538퍼센트
부하 위상 전압의 푸리에 분석:
과도 응답의 푸리에 성분 v(7,6)
직류성분 = -5.680E-10
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.195E+02 1.000000 0.000 0.000
2 1.200E+02 1.039E-09 0.000000 144.749 144.749
3 1.800E+02 1.251E-06 0.000000 89.974 89.974
4 2.400E+02 4.215E-10 0.000000 36.127 36.127
5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000
6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760
7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000
8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385
9 5.400E+02 3.752E-06 0.000000 89.905 89.905
총 고조파 왜곡 = 0.235702퍼센트
소스 위상 전류의 푸리에 분석:
과도 응답의 푸리에 성분 v(2,1)
직류성분 = -1.923E-12
고조파 주파수 푸리에 정규화 위상 정규화
없음(hz) 구성 요소 구성 요소(도) 위상(도)
1 6.000E+01 1.194E-01 1.000000 179.940 0.000
2 1.200E+02 2.569E-11 0.000000 133.491 -46.449
3 1.800E+02 3.129E-07 0.000003 89.985 -89.955
4 2.400E+02 2.657E-11 0.000000 23.368 -156.571
5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939
6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415
7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939
8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699
9 5.400E+02 9.385E-07 0.000008 89.991 -89.949
총 고조파 왜곡률 = 58.961298퍼센트
앞서 예측한 대로, 부하 위상 전압은 Δ-Δ 시스템에서 소스 위상과 직접 연결되기 때문에 고조파 성분이 무시할 수 있을 정도로 거의 순수 사인파입니다.
하지만 삼중 고조파는 어떻게 되었을까요? 3차 및 9차 고조파 주파수는 회선 전류, 부하 위상 전압, 소스 위상 전류에 실질적으로 나타나지 않습니다! 우리는 3차 및 9차 고조파 전류 소스가 부하 위상에 의도적으로 배치되었기 때문에 삼중 전류가 존재한다는 것을 알고 있지만, 그 전류는 어디로 갔을까요?
델타-델타 회로에서 삼중 고조파의 효과 분석
120° 위상이 이동된 기본 주파수의 3배 고조파는 서로 동상에 있다는 것을 기억하세요.
부하 단계 내 전류원의 화살표가 가리키는 방향을 주목하고, 3차 및 9차 고조파원이 대신 DC원이라면 무슨 일이 일어날지 생각해 보세요.
우리가 현재 가질 것은 Δ-연결된 위상에 의해 형성된 루프 내에서 순환하는 것 입니다 . 여기가 삼중 고조파 전류가 간 곳입니다. 이들은 부하의 Δ 내에 머물며, 결코 전선 도체나 소스의 권선에 도달하지 않습니다.
이러한 결과는 아래 그림과 같이 그래픽으로 요약될 수 있습니다.

Δ-Δ 소스/부하: 부하 위상은 왜곡되지 않은 사인파 전압을 수신합니다. 삼중 전류는 부하 위상 내에서 순환하도록 제한됩니다. 비삼중 전류는 라인 도체와 소스 위상 권선에 나타납니다.
이는 Δ-Δ 시스템 구성의 주요 이점입니다. 즉, 3배 고조파 전류는 이를 생성하는 구성 요소 집합에 국한되어 있으며 시스템의 다른 부분으로 "확산"되지 않습니다.
검토:
- 비선형 성분은 사인파(사인파) 전압에 의해 전원이 공급될 때 비사인파(사인파가 아닌) 전류 파형을 그리는 성분입니다. 원래 순수한 사인파의 왜곡은 고조파 주파수를 구성하므로 비선형 성분은 고조파 전류를 생성한다고 말할 수 있습니다.
- 사인파 왜곡이 파형의 평균 중심선을 기준으로 위아래로 대칭일 때, 존재하는 유일한 고조파는 짝수가 아닌 홀수입니다.
- 3차 고조파와 그 정수 배수(6차, 9차, 12차, 15차)는 3배 고조파로 알려져 있습니다. 이들은 각각의 기본 파형이 서로 120° 위상이 틀렸음에도 불구하고 서로 동상입니다.
- 4선식 YY 시스템에서는 중성선에 3배의 고조파 전류가 추가됩니다.
- Δ로 연결된 구성 요소 집합의 3배 고조파 전류는 Δ에 의해 형성된 루프 내부를 순환합니다.