부울 대수학 단순화
부울 대수 단순화 및 변수, 리터럴 및 용어에 적용되는 몇 가지 기본 규칙을 사용하여 부울 대수 표현식을 단순화하는 방법
부울 대수학 단순화는 " + " 및 " 의 기호 또는 기호의 사용을 인식하면 이해하기 어렵지 않습니다 . ”는 논리 함수의 동작을 나타냅니다.
논리 함수는 조건 또는 상태가 TRUE 또는 FALSE 인지 여부를 테스트 하지만 동시에 둘 다는 아닙니다. 따라서 해당 테스트 결과에 따라 디지털 회로는 한 가지 작업 또는 다른 작업을 수행하기로 결정할 수 있습니다.
부울 대수의 법칙 튜토리얼 에서 보았듯이 부울 대수는 논리의 수학이며 다양한 전환 이론 규칙을 적용하면 길거나 복잡한 전환 대수 표기법을 단순화할 수 있으며 논리 게이트 및 논리 게이트에도 적용할 수 있습니다. 기본 디지털 회로.
그러나 부울 대수학이 보다 복잡한 스위칭 네트워크를 단순화하는 데 어떻게 도움이 될 수 있는지 알아보기 전에 먼저 AND , OR 및 NOT 의 세 가지 주요 기능과 관련된 몇 가지 기본 기호, 의미 및 법칙을 상기해 보겠습니다 .
논리 AND 연산
AND 연산자에 대해 제공된 논리 또는 부울 표현식은 A 및 B 의 부울 표현식이 A*B 와 동일한 논리 곱 또는 부울 곱 에 대한 것입니다 . AND 연산자는 일반적으로 단일 점 또는 마침표 기호( . )로 표시됩니다. 이는 AB 또는 단순 AB 의 부울 표현식을 제공합니다 .
2입력 논리 AND 게이트

예를 들어, 입력 A, B, C가 있는 AND 게이트의 출력은 A x B x C(또는 ABC)로 작성되고 부울 곱 ABC는 "A 및 B 및 C"로 읽혀집니다.
그러나 ABC의 부울 곱은 CBA, A(BC) 또는 AB(C) 등으로 쓸 수도 있습니다. 이는 부울의 곱셈 결합 법칙을 따르는 것과 정확히 동일합니다.
그러면 두 개 이상의 입력 조건을 비교하고 모든 조건이 함께 발생하는 경우에만 TRUE를 반환하는 데 논리 AND 함수가 사용된다는 것이 분명합니다. 곱셈의 논리적 AND 연산은 직렬 연결된 스위치의 수에 관계없이 확장할 수 있으므로 스위치가 직렬로 연결되는 순서가 중요하지 않은 직렬 연결을 나타냅니다. 따라서 ABC의 부울 표현식은 대수 전환에서 다음과 같이 표시될 수 있습니다.
직렬(AND) 스위칭 표현

열린 스위치 조건을 "0"을 생성하는 비이벤트로 정의하고 스위치 폐쇄를 "1"을 생성하는 이벤트로 정의한다는 것을 기억하십시오. 또한 부울 표기법의 경우 두 개 이상의 유사한 용어를 "AND-ing"하면 부울의 멱등 법칙 에 따라 하나의 단일 용어가 생성됩니다 . 예: AA = A 또는 AAAA = A
논리 OR 연산
OR 연산자에 대해 제공된 논리 또는 부울 표현식은 A 또는 B 의 부울 표현식이 A+B 와 동일한 논리 합 또는 논리 합 에 대한 것입니다 . OR 연산자는 일반적으로 더하기 기호( + )로 표시되며 A+B 의 부울 표현식을 제공합니다 .
2입력 논리 OR 게이트
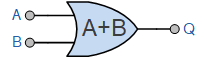
논리 OR 연산의 경우 세 개의 입력 A, B, C가 있는 경우 출력은 A + B + C로 작성되어 입력이 서로 추가되는 것을 보여줍니다. 부울 합계 A+B+C는 "A 또는 B 또는 C"로 읽히고 C+B+A 또는 B+A+C 또는 A+C+B 등으로 쓸 수도 있습니다. 이는 Boole의 덧셈 결합법칙을 따르는 것과 동일합니다.
그렇다면 논리 OR 함수는 두 개 이상의 입력 조건을 비교하는 데 사용되며 조건 중 하나가 발생하는 경우에만 TRUE를 반환한다는 것이 분명합니다. 추가의 논리적 OR 연산은 병렬 연결된 스위치의 수에 관계없이 확장할 수 있으므로 스위치가 병렬로 연결된 순서가 중요하지 않은 병렬 연결을 나타냅니다. 따라서 A+B+C의 부울 표현식은 대수 전환에서 다음과 같이 표시될 수 있습니다.
병렬(OR) 스위칭 표현
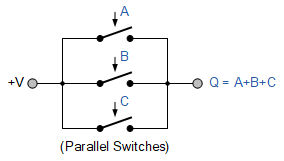
부울 표기법의 경우 두 개 이상의 유사한 용어를 "OR-ing"하면 다시 하나의 단일 용어가 생성됩니다. 이것이 바로 부울의 멱등 법칙 입니다 . 예: A+A = A 또는 A+A+A+A = A
논리 NOT 연산
논리적 NOT 연산은 단순히 부울 값의 반전 또는 보완 함수이며 별도의 변수로 간주되지 않습니다. NOT 함수 는 출력 상태가 입력 상태와 "NOT"이고 일반적으로 반전 연산을 나타내는 기호 위에 막대 또는 윗줄( )로 표시되는 부울 표현식을 사용하여 그렇게 불립니다. 따라서 이름은 인버터입니다. .
즉, 스위치 A 가 열려 있으면 A는 스위치가 닫혀 있다는 의미입니다. 즉, NOT 함수에 대한 부울 표현식은 입력이 "1"이면 출력이 "0"이고 입력이 "0"이면 출력이 "1"입니다.
부울 형식에서 반전은 보수 또는 반대 형식을 나타내는 A -bar 로 읽혀집니다. 또한 "이중 반전"( ̿ )은 두 개의 보완을 함께 나타냅니다. 이는 표현식을 변경하지 않고 표현식의 보수의 보수를 나타내기 때문에 A = A 입니다 . 이것이 원래의 표현(A)이다. 스위칭 회로에서 이 부정은 그림과 같이 일반적으로 닫힌 스위치로 표현될 수 있습니다.
표현이 아님
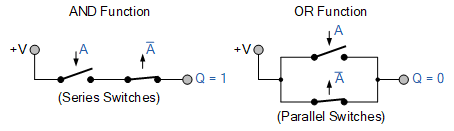
이중 반전 A , A 에 유의하세요 . A 와 A + A는 모두 부울의 보수 법칙을 나타냅니다 .
또한 부울 대수학에 관한 일부 책에서는 부울 값의 반전 또는 보완이 다음과 같이 표현됩니다. A' . 따라서 A 와 A'는 변수의 보수를 나타내기 위해 상호 교환적으로 사용될 수 있습니다.
부울 대수학 단순화
AND , OR 및 NOT 기능 의 전환 작업을 설정했습니다 . 이제 최소한의 항을 갖는 최종 표현식을 얻기 위해 몇 가지 기본 부울 대수 표현식을 단순화하는 방법을 살펴볼 수 있습니다.
먼저 다음과 같은 간단한 것부터 시작해 보겠습니다.
불리언 표현식: A.(A + B)
대괄호를 곱하면 다음과 같습니다.
| A.(A+B) | 시작 | |
| 곱하다: | AA + AB | 분배법칙 |
| 하지만: | AA = A | 멱등법칙 |
| 그 다음에: | A + AB | 절감 |
| 따라서: | A.(1 + B) | 무효화법 |
| 다음과 같습니다: | ㅏ | 흡수 법칙 |
그러면 A.(A + B)의 부울 표현이 부울의 흡수 법칙을 따르는 "A"로 축소될 수 있음을 알 수 있습니다 .
예시 2
이번에는 세 가지 부울 용어 A, B, C를 사용하고 이전과 동일한 부울 대수 단순화 규칙을 사용합니다.
부울 표현식: (A + B)(A + C)
다시, 괄호를 곱하면 다음과 같습니다.
| (A + B)(A + C) | 시작 | |
| 곱하다: | AA + AC + AB + BC | 분배법칙 |
| 하지만: | AA = A | 멱등법칙 |
| 그 다음에: | A + AC + AB + BC | 절감 |
| 하지만: | A + AC = A | 흡수 법칙 |
| 따라서: | A + AB + 기원전 | 분배법칙 |
| 다시: | A + AB = A | 흡수 법칙 |
| 따라서: | A + 기원전 | 결과 |
그런 다음 (A + B)(A + C)의 부울 표현은 다양한 부울 대수 법칙을 사용하여 "A + BC"로 축소될 수 있습니다.
부울 대수 단순화 예 No3
이번에는 A, B, C의 동일한 세 가지 부울 항을 다시 사용하지만 항 중 하나에 NOT 함수를 도입합니다.
불리언 표현: AB( B C + AC)
| AB( B C+AC) | 시작 | |
| 곱하다 | AB B .C + ABAC | 분배법칙 |
| 다시: | AA = A | 멱등법칙 |
| 그 다음에: | AB B .C + ABC | 절감 |
| 하지만: | B. B = 0 | 보완법 |
| 그래서: | A.0.C + ABC | 절감 |
| 다음과 같이 됩니다: | 0 + ABC | 절감 |
| 처럼: | 0 + ABC = ABC | 신원법 |
| 따라서: | 알파벳 | 결과 |
그런 다음 AB( B C+AC) 의 부울 표현은 "ABC"로 축소됩니다.
부울 대수 단순화 예 No4
이제 대수 표현을 가장 간단한 형태로 줄이기 위해 몇 가지 기본 부울 대수 법칙을 사용하여 부울 대수 용어를 단순화하는 방법에 대한 기본 아이디어를 갖게 되었습니다 . 따라서 다음과 같은 마지막 부울 대수 단순화 예제 에서 모든 것을 하나로 묶습니다 .
부울 표현식: (A + B + C )(A + B + C)(A + B + C )
다시 한번, 첫 번째 괄호를 곱하는 것부터 시작하겠습니다.
| (A+ B + C )(A+ B +C)(A+B+ C ) |
| A(A+ B +C)(A+B+ C ) + B (A+ B +C)(A+B+ C ) + C (A+ B +C)(A+B+ C ) |
| (AA+A B +AC)(AA+AB+A C ) + (A B + B B + B C )(A B +B B + B C ) + (A C + B C +C C )(A C + B C + C C ) |
| AA = A(멱등법칙) |
| B B = C C = 0 (보완법칙) |
| (A+A B +AC)(A+AB+A C ) + (A B + B + B C )(A B +0+ B C ) + (A C + B C +0)(A C +B 씨 + 씨 ) |
| A + AB = A (흡수 법칙) |
| A + AC = A (흡수 법칙) |
| A + 0 = A (동일성 법칙) |
| (A+AC)(A+AB+A C ) + (A B + B + B C )(A B + B C ) + (A C + B C )(A C +B C + C ) |
| A(A+AB+A C ) + ( B + B C )(A B + B C ) + (A C + B C )(B C + C ) |
| A(A+A C ) + B (A B + B C ) + C (A C + B C ) |
| AA + (A B + B B C ) + (A C C + B C C ) |
| A + (A B + B C ) + (A C + B C ) |
| A + (A B ) + ( B C ) + (A C ) |
| A + ( B C ) + ( A C ) |
| A + ( BC ) |
따라서 (A + B + C )(A + B + C)(A + B + C ) 의 복잡한 부울 표현식은 다음과 같은 더 작은 표현식으로 축소되었습니다. A + ( BC )
부울 대수 단순화 요약
우리는 이 부울 대수 단순화 튜토리얼에서 부울 대수 표현식을 단순화하는 목적이 최소 항 수를 갖는 최종 논리 표현식을 얻는 것임을 확인했습니다. 부울 함수는 AND, OR 및 NOT 연산자를 사용하여 형성된 대수식입니다.
A, B 및 C의 부울 변수는 함수의 리터럴 로 알려져 있으며 이 튜토리얼에서는 대문자 A, B 및 C를 사용했지만 리터럴은 기호 값을 가질 수 있습니다. 예를 들어 X,Y,Z 또는 a, b, c입니다. 따라서 모든 기호는 1 또는 0의 값을 가질 수 있는 논리 변수를 나타내는 데 사용될 수 있습니다.
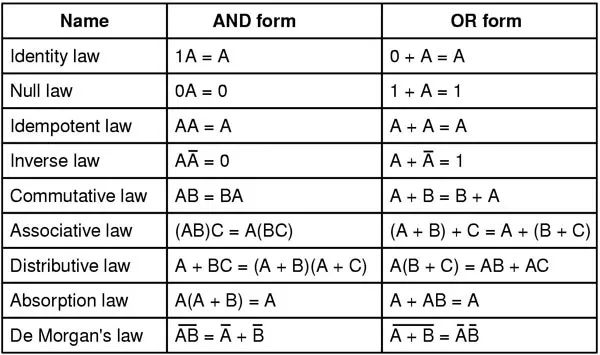
다음 부울 대수 단순화 표에 제시된 가장 일반적인 법칙을 사용하여 길거나 복잡한 표현 또는 조합 논리 회로를 훨씬 더 작은 회로로 줄이는 수단을 제공하는 여러 가지 부울 대수 법칙, 규칙 및 정리가 있습니다.
부울 대수 단순화 표
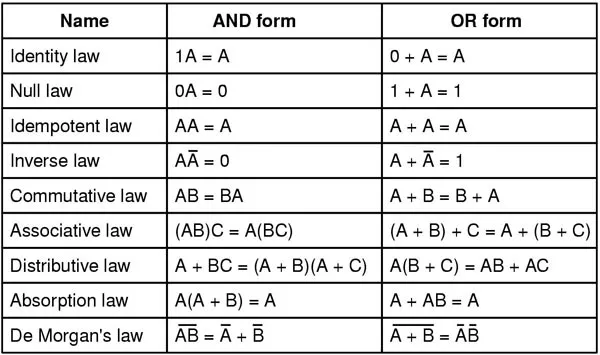
이러한 법률과 규칙 중 일부는 자명해 보일 수도 있고 그렇지 않은 경우도 있습니다. 조합 논리 회로 축소 또는 단순화 작업을 수행할 때 이들과 그 응용을 배우고 이해하는 것이 중요합니다.
그런 다음 부울 대수를 사용하여 모든 논리 회로를 원래 회로와 동일하게 기능하는 간단한 등가 회로로 줄일 수 있으며, 원래의 부울 표현식과 최종 부울 표현식의 동등성을 증명하기 위해 각각에 대해 비교할 진리표를 만들 수 있습니다. 진리표가 일치하면 최종 축소식이 올바른 것입니다.