
제품 합계
Sum of Product 표현식은 두 개 이상의 제품을 합산하여 출력을 생성하는 논리 AND 함수와 동일합니다.
부울 대수는 표준 논리 게이트의 전환 동작을 나타내는 간단하고 효과적인 방법이며 특정 논리 연산을 수행하는 데 필요한 논리 게이트 수를 줄이는 데 도움이 되는 일련의 규칙 또는 법칙이 발명되었습니다. 곱의 합(Sum-of-Product) 형식은 입력의 서로 다른 "곱" 용어를 함께 "합산"하는 부울 대수 표현입니다.
부울 대수학은 스위칭 이론에서 "풀 세트"라고도 알려진 AND , OR 및 NOT 게이트 기능 과 같은 게이트 및 스위칭 회로를 분석하는 데 사용하는 디지털 논리 수학입니다 .
표준 수학에서는 두 개 이상의 숫자를 곱하여 얻은 숫자 또는 수량을 곱이라고 합니다 . 예를 들어, 숫자 2에 3을 곱하면 결과는 6입니다. 즉 2*3 = 6이므로 "6"이 제품 번호가 됩니다.
부울 대수학에서 두 정수의 곱셈은 논리적 AND 연산과 동일하므로 두 개 이상의 입력 변수가 함께 " AND "될 때 "곱 " 항을 생성합니다. 즉, 부울 대수에서 AND 함수는 곱셈과 동일하므로 출력 상태는 입력의 곱을 나타냅니다.
AND 게이트(제품)

곱셈 동작을 나타내기 위해 십자형 ( x ) 또는 별 ( * ) 을 사용하는 기존 수학과 달리 AND 함수는 단일 "점"( . )으로 부울 곱셈으로 표현됩니다. 따라서 2-입력 AND 게이트에 대한 부울 방정식은 다음과 같이 제공됩니다. Q = AB, 즉 Q는 A AND B와 같습니다. 제품 용어의 경우 이러한 입력 변수는 "true" 또는 "false", "1" 또는 "false"일 수 있습니다. "0"이거나 보완 형식이므로 AB , A. B 또는 A 입니다 . B는 모두 제품 용어로 분류됩니다.
제품(AND) 용어
따라서 우리는 이제 부울 대수학에서 "곱"은 결과 곱이 더 이상 단순화될 수 없도록 실제 형태 또는 보수 형태의 하나의 인스턴스를 갖는 곱 용어의 변수와 용어의 AND' 를 의미한다는 것을 알고 있습니다. 이것을 minterms 이라고 합니다 . 그렇다면 부울 대수학에서 이 "제품" 함수의 작동을 어떻게 보여줄 수 있습니까?
곱 항은 A 및 B 와 같은 하나 또는 두 개의 독립 변수를 가질 수도 있고 , 다시 0 및 1 과 같은 하나 또는 두 개의 고정 상수를 가질 수도 있습니다 . 이러한 변수와 상수를 다양한 조합으로 사용할 수 있으며 다음 목록에 표시된 대로 제품 결과를 생성할 수 있습니다.
부울 대수학 제품 용어
- 변수와 상수
- ㅏ . 0 = 0
- ㅏ . 1 = A
- ㅏ . A = A
- ㅏ . A = 0
- 상수만
- 0 . 0 = 0
- 0 . 1 = 0
- 1 . 0 = 0
- 1 . 1 = 1
부울 "변수"는 "1" 또는 "0"의 두 값 중 하나를 가질 수 있으며 해당 값을 변경할 수 있습니다. 예를 들어, A = 0 또는 A = 1인 반면 "1" 또는 "0" 형태일 수도 있는 부울 "상수"는 고정된 값이므로 변경할 수 없습니다.
그런 다음 "A"가 변수 입력을 나타내는 아래에 제공된 다양한 부울 법칙에 대한 간략한 설명을 통해 특정 부울 곱을 단일 상수 또는 변수로 단순화할 수 있음을 알 수 있습니다.
- 무효법 – 0으로 AND된 용어는 항상 0과 같습니다(A.0 = 0).
- 동일성 법칙 – 1로 AND된 용어는 항상 용어와 같습니다(A.1 = A).
- 멱등 법칙 - 자신과 AND로 연결된 용어는 항상 용어와 같습니다(AA = A).
- 보수법칙 – 보수와 AND로 연결된 항은 항상 0과 같습니다(A. A = 0).
- 교환 법칙 – 두 항이 AND로 연결된 순서는 동일합니다(A.1 = 1.A).
합계(OR) 항
일반적으로 AND 함수를 곱항이라고 하는 반면 , OR 함수는 합계항이라고 합니다. OR 함수 는 더하기 기호( + )로 표시되는 덧셈과 수학적으로 동일합니다. 따라서 2-입력 OR 게이트는 A 와 B 의 논리합이기 때문에 A + B 의 부울 표현식으로 표시되는 출력 항을 갖습니다 .
OR 게이트(합)

OR 함수가 두 개 이상의 입력 변수 또는 상수의 합산 항을 생성하므로 이 논리합은 일반적으로 부울 덧셈으로 알려져 있습니다 . 다음 튜토리얼에서 OR 함수와 부울 덧셈을 더 자세히 살펴보겠습니다 . 하지만 지금은 OR 함수가 Sum Term 을 나타낸다 는 점을 기억하겠습니다 .
제품 합계
따라서 우리는 AND 함수가 부울 곱셈의 논리적 곱을 생성하고 OR 함수가 부울 덧셈의 논리적 합을 생성한다는 것을 확인했습니다 . 그러나 AND 게이트, OR 게이트, NOT 게이트가 함께 연결된 조합 논리 회로를 다룰 때에는 곱의 합( Sum-of-Products) 과 합의 곱(Product-of-Sums) 이라는 표현이 널리 사용됩니다.
SOP( Sum of Product ) 표현은 둘 이상의 곱(AND)을 함께 합(OR)한다는 사실에서 유래합니다. 즉, 두 개 이상의 AND 게이트의 출력이 OR 게이트 의 입력에 연결되어 효과적으로 OR되어 최종 AND-OR 논리 출력을 생성합니다. 예를 들어, 다음 부울 함수는 일반적인 곱셈 표현식입니다.
제품표현의 합
Q = (AB) + ( B .C) + (A.1)
그리고 또한
(ABC) + (AC) + ( B . C )
그러나 부울 함수는 아래 그림과 같이 비표준 곱의 합 형식으로 표현할 수도 있지만, 표현을 확장하면 표준 SOP 형식으로 변환할 수도 있습니다. 그래서:
Q = A. B ( C + C) + ABC
제품 합계 기준으로 다음과 같습니다.
Q = A.B . C + A. B .C + ABC
실제로 이 큰 SOP 표현은 부울 대수학의 법칙을 사용하여 다음과 같이 축소된 SOP 표현을 제공함으로써 더욱 축소될 수 있습니다.
Q = A. B + AC
SOP 표현식을 진리표로 변환
논리 "1" 출력을 생성하는 각 입력 조합은 아래와 같이 AND 또는 곱 항 이므로 진리표 형식으로 곱의 합계 항을 표시할 수 있습니다 .
제품 표현의 다음 합계를 고려하십시오 .
Q = AB C + A. B .C + A .BC
이제 위 표현식에 대한 진리표를 작성하여 A , B 및 C 에 대해 가능한 모든 입력 조합 목록을 표시할 수 있으며 결과는 "1"입니다.
제품 진리표 형식의 합계
| 입력 | 산출 | 제품 | ||
| 씨 | 비 | ㅏ | 큐 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | AB C |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | A.B.C _ _ |
| 1 | 1 | 0 | 1 | A.BC _ |
| 1 | 1 | 1 | 0 | |
그런 다음 출력에 대해 "1"을 생성하는 각 곱 행은 부울 곱셈 표현식에 해당하고 "0" 출력을 "1"로 갖는 다른 모든 행은 항상 다음에서 출력된다는 사실을 진리표에서 명확하게 볼 수 있습니다. OR 게이트.
여기서 분명한 이점은 진리표가 부울 표현식의 시각적 표시를 제공하여 표현식을 단순화할 수 있다는 것입니다. 예를 들어, 위의 곱의 합계 항은 필요한 경우 Q = A.(B + B .C) 로 단순화될 수 있습니다.
곱셈의 예
다음 부울 대수 표현식은 다음과 같이 제공됩니다.
Q = A ( BC + BC + BC ) + ABC
1. 이 논리 방정식을 동등한 SOP 용어로 변환합니다.
2. 진리표를 사용하여 출력을 생성할 입력 조건의 가능한 모든 조합을 표시합니다.
3. 표현식에 대한 논리 게이트 다이어그램을 그립니다.
1. SOP 용어로 전환
Q = ABC + A . B .C + A .BC + A .B. 씨
2. 진리표
제품 진리표 형식의 합계
| 입력 | 산출 | 제품 | ||
| 씨 | 비 | ㅏ | 큐 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | A.B. _ 씨 |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | ㅏ . 기원전 .C |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | A.BC _ |
| 1 | 1 | 1 | 1 | 알파벳 |
3. 논리 게이트 SOP 다이어그램
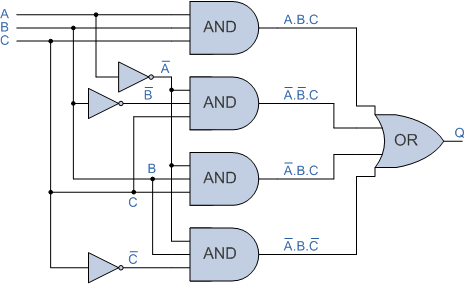
그런 다음 이 튜토리얼에서 SOP( Sum-of-Products ) 표현식은 두 개 이상의 "곱"을 "합산"하는 표준 부울 표현식이고 디지털 논리 회로의 경우 SOP 표현식은 두 개 이상의 "곱"의 출력을 취한다는 것을 확인했습니다. 논리 AND 게이트와 OR을 함께 사용하여 최종 (AND-OR) 출력을 생성합니다.