스위칭 이론

스위칭 이론

스위칭 이론은 스위치를 사용하여 디지털 회로의 논리 설계를 위한 부울 표현식과 논리 게이트를 구현하는 것에 관한 것입니다.

스위칭 이론을 통해 우리는 디지털 논리 게이트 와 관련하여 부울 대수와 2단계 논리 함수 간의 작동 및 관계를 이해할 수 있습니다 . 스위칭 이론은 출력 상태 또는 조건을 생성하는 입력 요소의 상호 연결로 볼 때 디지털 회로의 이론적 지식과 개념을 더욱 발전시키는 데 사용될 수 있습니다.

입력과 출력이 0 과 1 의 서로 다른 두 논리 값 사이에서 전환될 수 있는 디지털 논리 게이트는 부울 대수를 사용하여 수학적으로 간단하게 정의할 수 있습니다. 그러나 TRUE 또는 FALSE뿐만 아니라 HIGH 또는 LOW, "1" 또는 "0", "ON" 또는 "OFF"의 두 가지 디지털 논리 상태를 나타낼 수도 있습니다.

이러한 논리적 상태는 스위치 또는 릴레이 형태의 전기 기계 접점을 논리 회로 요소로 사용하여 나타낼 수 있습니다. 디지털 논리 회로에서 스위칭 기능을 구현하는 것은 새로운 것은 아니지만 단일 디지털 논리 게이트가 작동하는 방식을 더 잘 이해할 수 있게 해줍니다.

디지털 논리 게이트는 모든 디지털 전자 회로와 마이크로프로세서 기반 시스템이 만들어지는 기본 빌딩 블록입니다. 이들은 서로 연결되어 적용된 외부 입력 신호에 완전히 의존하는 조합 논리 회로 또는 현재의 안정적인 상태, 출력 피드백 및 외부 입력 신호에 의존하는 순차 논리 회로를 형성할 수 있습니다. 전환 이벤트를 트리거할 수 있습니다.

 

스위치의 스위칭 이론

스위치는 조명 부하를 "ON" 또는 "OFF"로 전환하는 데 사용할 수 있는 스위치라고 생각할 수도 있습니다. 그러나 스위치는 어느 방향으로든 신호 흐름을 제어하는 ​​데 사용되는 복잡한 기계 또는 전기 기계 요소일 수도 있으므로 양방향 장치가 될 수 있습니다. 표시된 회로를 고려하십시오.

상시 개방형 스위치의 스위칭 이론

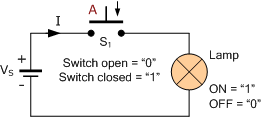
이 간단한 예에서 램프( L )는 상시 개방 스위치 S 1 을 통해 배터리 공급 V S 에 연결됩니다 .

따라서 스위치 S1 을 누르지 않아 열리면 전류(I)가 흐르지 않으므로 램프가 "OFF"되고 켜지지 않습니다. 마찬가지로 스위치 S1 을 눌러 닫으면 전류가 회로 주위로 흐르고 램프( L )가 "ON"되어 켜집니다. 정상적인 정상 상태 조건에서는 스위치가 영구적으로 "열려" 있으므로 램프도 "꺼집니다".

스위치 S 1 을 포함하는 회로의 동작을 설명하기 위해 스위칭 대수학을 사용할 수 있습니다 . 예를 들어, 일반적으로 열려 있는 스위치에 문자 " A "를 사용하여 변수로 레이블을 지정하면 스위치가 열려 있을 때, 즉 "A"가 눌려지지 않은 경우 "A"의 값을 "로 정의할 수 있습니다. 0”. 다시, 스위치가 닫힐 때, 즉 “A”를 누르면 “A”의 값을 “1”로 정의할 수 있습니다. 이 스위칭 대수 이론은 모든 정상 개방 스위치 구성에 적용됩니다.

진리표 전환

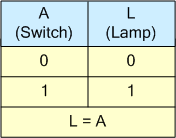
램프가 "ON"(켜짐)일 때 스위칭 대수 변수는 "1"이 되고 램프가 "OFF"(켜지지 않음)일 때 스위칭 대수 변수는 "1"이 될 것이라고 말함으로써 이 스위칭 이론 아이디어를 더욱 발전시킬 수 있습니다. “0”.

따라서 스위치를 누르면(활성화) 램프가 "ON"되므로 "A" = 1, "L" = 1이고, 스위치를 누르지 않으면(비활성화) 램프가 "OFF"이므로 " A” = 0이고 “L” = 0입니다. 따라서 램프의 스위칭 이론에 대해 진리표에 표시된 대로 L = A 라고 정확하게 말할 수 있습니다.

위의 예에 사용된 스위치 유형은 스위치가 닫힌 것으로 간주되도록 물리적으로 만들어야 하기 때문에 상시 개방형, 접점 투입 스위치라고 합니다(A = 1). 그러나 위의 스위치 작동과 정반대로 항상 닫혀 있는 상시 폐쇄, 차단 접점 스위치 라고 불리는 또 다른 유형의 스위치 배열이 있습니다 .

시리즈 스위치의 스위칭 이론

위의 램프( L ) 회로는 단일 스위치 S1 을 사용하여 제어할 수 있으며 S1 이 닫히면(눌려지면) 전류가 회로 주위로 흐르고 램프가 "ON"되는 것을 확인했습니다 . 그러나 S 1 과 직렬로 두 번째 스위치를 추가하면 회로의 스위칭 기능과 램프 조명에 어떤 영향을 미칠까요?

시리즈 스위치의 스위칭 이론

 

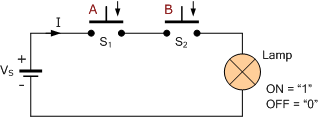
스위칭 회로는 전압원 V S 및 램프와 직렬로 연결된 두 개의 스위치로 구성됩니다. 각 개별 스위치의 작동을 구별하기 위해 스위치 S 1 에 문자 " A "를 표시하고 스위치 S 2 에 문자 " B "를 표시합니다. 따라서 두 스위치 중 하나가 열려 있으면, 즉 누르지 않은 경우 "A" 값을 "0"으로 정의하고 "B" 값도 "0"으로 정의할 수 있습니다.

마찬가지로, 스위치 중 하나를 닫거나 눌렀을 때 "A"의 값을 "1"로 정의하거나 "B"의 값을 "1"로 정의할 수 있습니다. 즉, 논리 레벨 "1"은 공급 전압 값에 해당하며 양수입니다. 논리 레벨 "0"은 0 전압 또는 접지의 전압 값에 해당합니다.

S 1 과 S 2 또는 "A"와 "B" 라는 두 개의 스위치가 있으므로 램프를 켜기 위해 부울 변수 "A"와 "B"의 네 가지 가능한 조합이 있음을 알 수 있습니다. 예를 들어, “A”가 열려 있고 “B”가 닫혀 있거나, “A”가 닫혀 있고 “B”가 열려 있거나, “A”와 “B”가 동시에 열리거나 닫혀 있는 경우 등이 있습니다. 그런 다음 다음 전환 이론 진리표에서 이러한 작업을 정의할 수 있습니다.

시리즈 스위치 진리표

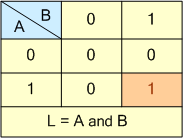
진리표는 스위치 A 와 스위치 B 를 모두 누르고 닫을 때만 램프가 "ON"되고 조명이 켜진다는 것을 보여줍니다. 하나의 스위치만 누르면 전류가 흐르지 않기 때문입니다.

 

이는 두 개의 스위치 S1 과 S2 가 직렬로 연결될 때 전류(I)가 흐르고 램프가 켜지는 유일한 조건은 두 스위치가 모두 닫혀 다음과 같은 부울 식을 제공할 때라는 것을 증명합니다. L = A 및 B .

부울 대수 용어에서 이 표현식은 다음과 같은 부울 표현식을 제공하는 변수 사이에 단일 점 또는 마침표 기호( . )로 표시되는 AND 함수의 표현식입니다. L = AB .

따라서 스위치가 직렬로 함께 연결되면 스위칭 이론과 작동은 디지털 논리 "AND" 게이트와 동일합니다. 왜냐하면 두 입력이 모두 "1"이면 출력은 "1"이고, 그렇지 않으면 출력은 "0"이기 때문입니다. 표시됩니다.

디지털 논리 AND 게이트

 

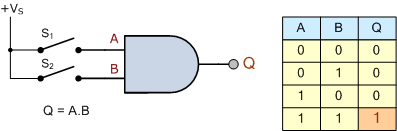
따라서 입력 "A"가 입력 "B"와 AND'되면 출력 "Q"가 생성됩니다. 전환 용어로 AND 함수를 부울 대수 곱셈 함수라고 합니다.

병렬 스위치의 스위칭 이론

이제 그림과 같이 스위치 S1 과 S2 를 병렬로 연결하면 배열이 회로의 스위칭 기능과 램프 조명에 어떤 영향을 미칠까요 ?

병렬 스위치의 스위칭 이론

 

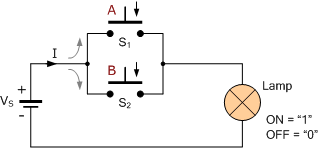
이제 스위칭 회로는 전압원 V S 및 램프와 병렬로 연결된 두 개의 스위치로 구성됩니다. 이전과 마찬가지로 두 스위치 중 하나가 열려 있으면(눌리지 않은 경우) "A" 값을 "0"으로 정의하고 "B" 값도 "0"으로 정의할 수 있습니다. 마찬가지로, 스위치 중 하나를 닫거나 눌렀을 때 "A"의 값을 "1"로 정의하거나 "B"의 값을 "1"로 정의할 수 있습니다.

이전과 마찬가지로 S 1 과 S 2 또는 "A"와 "B"라는 두 개의 스위치를 사용하면 램프를 켜는 데 필요한 부울 변수 "A"와 "B"의 네 가지 조합이 가능합니다. 해당 상태는 다음과 같습니다. "A"는 열려 있고 "B"는 닫혀 있습니다. 또는 "A"는 닫혀 있고 "B"는 열려 있고 "A"와 "B"는 모두 열려 있거나 둘 다 동시에 닫혀 있습니다. 그런 다음 다음 스위칭 이론 진리표에서 이러한 스위칭 작업을 정의할 수 있습니다.

병렬 스위치 진리표

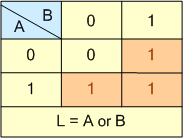
진리표는 스위치, A 또는 스위치, B 중 하나를 눌렀다가 닫을 때만 램프가 "ON"되고 조명된다는 것을 보여줍니다. 왜냐하면 두 스위치 중 하나를 누르면 전류가 흐르기 때문입니다. 램프를 통해 항상 램프에 사용 가능한 전도 경로가 있기 때문입니다. 어떤 스위치를 닫았든.

따라서 두 개의 스위치 S1 과 S2 를 병렬로 연결할 때 전류(I)가 흐르고 램프가 켜지는 스위칭 조건 은 스위치 중 하나 또는 둘 다 닫힐 때라는 것을 증명합니다. 이는 L = A 또는 B의 부울 표현식을 제공합니다.

부울 대수 용어에서 이 표현식은 L = A+B 의 부울 표현식을 제공하는 변수 사이에 추가 또는 더하기 기호( + )로 표시되는 OR 함수의 표현식입니다 .

따라서 스위치가 병렬로 함께 연결되면 스위칭 이론과 작동은 디지털 논리 "OR" 게이트와 동일합니다. 왜냐하면 두 입력이 모두 "0"이면 출력은 "0"이고 그렇지 않으면 출력은 "1"이기 때문입니다. 표시됩니다.

디지털 로직 OR 게이트

 

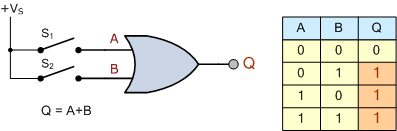
따라서 입력 "A"가 입력 "B"와 OR이면 출력 "Q"가 생성되고 전환 용어로 OR 함수를 부울 대수 논리 덧셈 함수라고 합니다.

부울 함수의 스위칭 이론

스위칭 이론은 부울 표현식과 디지털 논리 게이트를 구현하는 데 사용될 수 있습니다. 위에서 본 광고에서 스위치 접촉 용어로 점( . )을 사용하는 부울 표현식은 부울 곱셈을 위한 직렬 연결로 해석되는 반면, 더하기 기호( + )는 부울 덧셈을 위한 한 쌍의 병렬 분기로 해석됩니다.

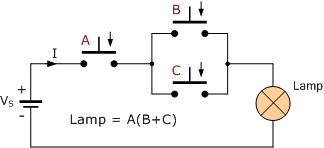
스위칭 이론 예 No1

램프(또는 LED)를 켜는 스위치를 사용하여 Q = A(B+C) 의 다음 부울 함수를 구현합니다 . 또한 등가 디지털 논리 회로를 보여주십시오.

스위치 구현

 

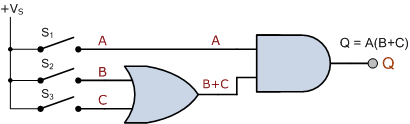
논리 게이트 구현

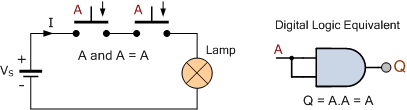
스위치의 멱등법칙

지금까지 우리는 두 개의 스위치를 직렬 또는 병렬로 연결하여 램프를 켜는 방법을 살펴보았습니다. 그러나 부울 AND 함수 또는 OR 함수(곱셈과 합 연산)를 나타내는 두 개의 스위치가 동일한 단일 부울 변수 A 에 속한다면 어떻게 될까요 ? 부울 대수학에는 논리 회로의 수학을 정의하는 데 사용할 수 있는 다양한 법칙과 이론이 있습니다. 그러한 정리 중 하나는 횡령법(Indempotent Law) 이라는 이름으로 알려져 있습니다 .

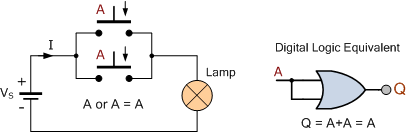
전환 이론에 사용되는 멱등 법칙은 변수 자체를 AND 또는 OR하면 원래 변수를 생성한다고 말합니다. 예를 들어 변수 "A" AND'와 "A"는 "A"를 제공하고 마찬가지로 변수 "A"와 "A"를 OR하면 "A"를 제공하여 스위칭 회로를 단순화할 수 있으며 아래에서 이를 시연할 수 있습니다. .

AND 함수의 무능한 법칙

 

OR 함수의 무능한 법칙

 

우리는 이 튜토리얼에서 스위칭 이론 기술을 사용하여 간단한 "ON/OFF" 스위치를 사용하여 부울 표현식과 디지털 논리 게이트 회로를 실현할 수 있다는 것을 확인했습니다.

상시 개방형 스위치를 사용한 "AND" 및 "OR" 기능 표현은 구성하기 쉽고 이해하기 쉬우며 대부분의 조합 논리 회로의 기본 빌딩 블록을 형성합니다.

따라서 불리언 표현이나 논리 함수가 주어지면 스위칭 이론을 사용하여 이를 구현하는 것이 가능합니다. 결국 논리 설계는 스위치나 릴레이와 같은 전기 기계 장치를 사용하는 것입니다.