
부울 대수학 예
부울 대수학 법칙을 사용하여 디지털 게이트 수를 줄이는 방법에 대한 부울 대수학 예
이 부울 대수 예제 튜토리얼에서는 부울 대수 법칙을 사용하여 디지털 로직 설계 내에서 불필요한 로직 게이트를 식별하여 전력 소비와 비용을 모두 절약하는 데 필요한 게이트 수를 줄일 수 있음을 살펴보겠습니다.
우리는 이 섹션 전체에서 디지털 논리 함수가 부울 대수 표현이나 논리 게이트 진리표로 정의되고 표시될 수 있다는 것을 살펴보았습니다. 따라서 여기에 부울 대수를 사용하여 더 큰 디지털 논리 회로를 단순화할 수 있는 방법에 대한 몇 가지 예가 있습니다 .
부울 대수학 예제 No1
다음 회로의 C , D , Q 지점에서 논리 기능에 대한 진리표를 구성 하고 전체 회로를 대체하는 데 사용할 수 있는 단일 논리 게이트를 식별합니다.

첫 번째 관찰에 따르면 회로는 2입력 NAND 게이트, 2입력 EX-OR 게이트, 마지막으로 출력의 2입력 EX-NOR 게이트로 구성됩니다. A 와 B 로 표시된 회로에는 2개의 입력만 있으므로 입력(2 2 )에는 4개의 가능한 조합만 있을 수 있으며 이는 0-0 , 0-1 , 1-0 및 마지막으로 1-1 입니다 . 각 게이트의 논리 함수를 표 형식으로 플롯하면 아래 논리 회로 전체에 대해 다음과 같은 진리표가 제공됩니다.
| 입력 | 출력 위치 | |||
| ㅏ | 비 | 씨 | 디 | 큐 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
위의 진리표에서 C 열은 NAND 게이트 에 의해 생성된 출력 함수를 나타내고 , D 열은 Ex-OR 게이트 의 출력 함수를 나타냅니다 . 이 두 출력 표현식은 모두 출력에서 Ex-NOR 게이트 의 입력 조건이 됩니다 .
두 개의 입력 A 또는 B 중 하나가 논리 1 에 있을 때 Q 의 출력이 존재한다는 것을 진리표에서 볼 수 있습니다 . 이 조건을 만족하는 유일한 진리표는 OR 게이트의 진리표입니다. 따라서 위 회로 전체는 단 하나의 단일 2입력 OR 게이트로 대체될 수 있습니다.
부울 대수학 예제 No2
다음 시스템에 대한 부울 대수 표현식을 찾으십시오.

시스템은 AND 게이트, NOR 게이트 및 마지막으로 OR 게이트로 구성됩니다. AND 게이트 의 표현식 은 AB 이고 NOR 게이트 의 표현식은 A+B 입니다 . 이 두 표현식은 모두 A+B 로 정의된 OR 게이트에 대한 별도의 입력이기도 합니다 . 따라서 최종 출력 표현식은 다음과 같이 제공됩니다.

시스템의 출력은 Q = (AB) + ( A+B )로 주어지지만 A+B 표기법은 De Morgan 표기법 A 와 동일합니다 . B , 그런 다음 A 로 대체합니다 . B 를 출력 표현식에 추가하면 Q = (AB)+( A . B )의 최종 출력 표기법이 제공됩니다. 이는 이전 섹션에서 본 Exclusive-NOR 게이트 에 대한 부울 표기법입니다 .
| 입력 | 중간체 | 산출 | ||
| 비 | ㅏ | AB | A + B | 큐 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
그런 다음 위의 전체 회로는 단 하나의 Exclusive-NOR 게이트로 대체될 수 있으며 실제로 Exclusive-NOR 게이트는 이러한 개별 게이트 기능으로 구성됩니다.
예시 3
다음 시스템에 대한 부울 대수 표현식을 찾으십시오.

이 시스템은 분석하기가 다른 두 시스템보다 더 복잡해 보일 수 있지만 논리 회로는 함께 연결된 간단한 AND , OR 및 NOT 게이트로 구성됩니다.
이전 부울 예제와 마찬가지로 Q 출력에 대한 최종 표현을 제공하기 위해 각 논리 게이트 함수에 대한 부울 표기법을 차례로 기록하여 회로를 단순화할 수 있습니다 .
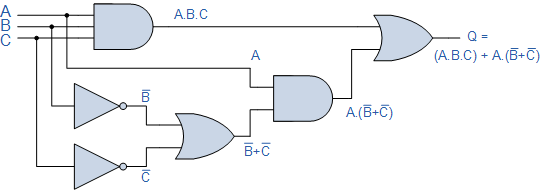
3입력 AND 게이트의 출력은 모든 게이트 입력이 로직 레벨 "1"( ABC )에서 HIGH인 경우에만 로직 "1"입니다 . 하단 OR 게이트의 출력은 입력 B 또는 C 중 하나 또는 둘 다 논리 레벨 "0"일 때만 "1"입니다. 2입력 AND 게이트의 출력은 입력 A 가 "1"이고 입력 B 또는 C 가 "0"일 때 "1"입니다. 그런 다음 입력 ABC가 " 1 " 이거나 A 가 "1"이고 두 입력 B 또는 C 가 모두 "0"인 경우 Q의 출력은 "1"입니다. A.( B + C ) .
" 드 모건의 정리 "를 사용하면 입력 B 와 입력 C가 상쇄되어 Q 에서 출력을 생성 하므로 논리 "1" 또는 논리 "0"이 될 수 있습니다. 그런 다음 아래 표에 표시된 대로 입력 A를 Q 에서 출력을 제공하는 데 필요한 유일한 입력으로 남겨 둡니다.
| 입력 | 중간체 | 산출 | ||||||
| 씨 | 비 | ㅏ | 알파벳 | 비 | 씨 | 비 + 씨 | A.( B + C ) | 큐 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
그러면 위의 전체 논리 회로가 " A " 라고 표시된 단 하나의 입력으로 대체되어 6개의 개별 논리 게이트 회로가 단 하나의 와이어(또는 버퍼)로 축소될 수 있음을 알 수 있습니다. 부울 대수를 사용하는 이러한 유형의 회로 분석은 매우 강력하고 디지털 논리 설계 내에서 불필요한 논리 게이트를 신속하게 식별하여 필요한 게이트 수, 회로의 전력 소비 및 비용을 줄일 수 있습니다.
'전자일기' 카테고리의 다른 글
| 스위칭 이론 (0) | 2024.01.28 |
|---|---|
| 드모건의 정리 (1) | 2024.01.28 |
| 부울 대수학 진리표 (0) | 2024.01.28 |
| 부울 대수학의 법칙 (0) | 2024.01.28 |
| 논리 NOR 기능 (0) | 2024.01.28 |