
비동기 카운터
비동기 카운터는 입력 클록 펄스가 카운터를 통해 리플하는 것처럼 보이도록 직렬로 연결된 플립플롭을 사용합니다.
비동기 카운터는 2 n -1 가능한 카운팅 상태를 가질 수 있습니다 (예: 4비트 카운터의 경우 MOD-16(0-15)). 이는 주파수 분할 애플리케이션에 사용하기에 이상적입니다. 그러나 기본 비동기 카운터 구성을 사용하여 최대 출력 수보다 적은 계산 상태로 특수 카운터를 구성하는 것도 가능합니다. 예를 들어 모듈로 또는 MOD 카운터입니다.
이는 시퀀스가 잘린 비동기 카운터 유형을 생성하는 미리 결정된 값에서 카운터가 강제로 0으로 재설정되도록 함으로써 달성됩니다. 그런 다음 최대 모듈러스( 2n ) 까지 계산하는 n비트 카운터 를 전체 시퀀스 카운터라고 하고 모듈러스가 가능한 최대값보다 작은 n비트 카운터를 잘린 카운터 라고 합니다 .
그런데 왜 MOD-4, MOD-8 또는 2의 거듭제곱과 같은 다른 계수가 아닌 비동기식 잘린 카운터를 생성하려고 합니까? 대답은 조합 논리를 사용하여 플립플롭의 비동기 입력을 활용할 수 있다는 것입니다.
모듈로 16 비동기 카운터를 추가 논리 게이트로 수정하면 표준 십진수 계산 및 산술 회로에 사용할 수 있는 10진수(10으로 나누기) 카운터 출력을 제공할 수 있습니다.
이러한 카운터를 일반적으로 Decade Counter(디케이드 카운터) 라고 합니다 . 10진 카운터는 출력 카운트가 10진수 값 10에 도달할 때 0으로 재설정해야 합니다. DCBA = 1010일 때 이를 수행하려면 이 조건을 재설정 입력에 다시 공급해야 합니다. 이진수 "0000"(BCD = "0")부터 "1001"(BCD = "9")까지의 카운트 시퀀스를 갖는 카운터는 일반적으로 10가지 상태 시퀀스이므로 BCD 이진 코드 십진수 카운터라고 합니다. BCD 코드이지만 이진 10년 카운터가 더 일반적입니다.
비동기식 10년 카운터

이 유형의 비동기 카운터는 0000부터 시작하여 출력 1001(10진수 9)에 도달할 때까지 입력 클록 신호의 각 후행 에지에서 위쪽으로 카운트됩니다. 이제 출력 QA와 QD 모두 논리 "1"과 같습니다. 다음 클록 펄스가 적용되면 74LS10 NAND 게이트의 출력은 논리 "1"에서 논리 "0" 레벨로 상태를 변경합니다.
NAND 게이트의 출력이 모든 74LS73 JK 플립플롭의 CLEAR( CLR ) 입력에 연결되므로 이 신호로 인해 모든 Q 출력이 10 카운트에서 이진수 0000 으로 다시 재설정됩니다. 출력 QA 및 플립플롭이 방금 재설정되었기 때문에 QD 는 이제 둘 다 논리 "0"과 같습니다. NAND 게이트의 출력은 논리 레벨 "1"로 돌아가고 카운터는 0000 에서 다시 시작됩니다 . 이제 10년 또는 Modulo-10 업 카운터가 있습니다.
10년 반대 진리표
| 클럭 카운트 | 출력 비트 패턴 | 소수값 | |||
| QD | 품질관리 | QB | 품질보증 | ||
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 |
| 삼 | 0 | 0 | 1 | 0 | 2 |
| 4 | 0 | 0 | 1 | 1 | 삼 |
| 5 | 0 | 1 | 0 | 0 | 4 |
| 6 | 0 | 1 | 0 | 1 | 5 |
| 7 | 0 | 1 | 1 | 0 | 6 |
| 8 | 0 | 1 | 1 | 1 | 7 |
| 9 | 1 | 0 | 0 | 0 | 8 |
| 10 | 1 | 0 | 0 | 1 | 9 |
| 11 | 카운터는 출력을 다시 0으로 재설정합니다. | ||||
디케이드 카운터 타이밍 다이어그램

카운터 출력 시퀀스를 자르는 동일한 아이디어를 사용함으로써 위의 회로는 단순히 NAND 게이트 의 입력에 대한 연결을 변경하거나 다른 논리 게이트 조합을 사용하여 다른 계산 사이클에 쉽게 적용할 수 있습니다.
예를 들어, " QC " 및 " QD " 의 출력에서 NAND 게이트 로의 입력을 가져오기만 하면 12 스케일(모듈로 12)을 쉽게 만들 수 있습니다 . 12에 해당하는 이진수는 1100 이고 출력 " QA "는 최하위 비트(LSB)입니다.
n개의 플립플롭 으로 구현할 수 있는 최대 모듈러스는 2n 이므로 , 이는 절단된 비동기 카운터를 설계할 때 원하는 모듈러스보다 크거나 같은 2의 최저 전력을 결정해야 함을 의미합니다.
0부터 39까지 또는 mod-40까지 계산하고 반복한다고 가정해 보겠습니다. 그렇다면 필요한 최대 플립플롭 수는 6개가 될 것입니다. n = 6은 최대 MOD 64를 제공합니다. 왜냐하면 5개의 플립플롭만으로는 충분하지 않기 때문입니다. 이는 MOD-32만 제공하기 때문입니다.
이제 주파수 분할을 위한 "128로 나누기" 카운터를 구축하려면 128 = 2 7 이므로 7개의 플립플롭을 계단식으로 연결해야 합니다 . 74LS74와 같은 듀얼 플립플롭을 사용하더라도 회로를 완성하려면 4개의 IC가 필요합니다.
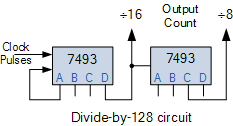
한 가지 쉬운 대안 방법은 두 개의 TTL 7493을 4비트 리플 카운터/분배기로 사용하는 것입니다. 128 = 16 x 8이므로 하나의 7493은 "16으로 나누기" 카운터로 구성하고 다른 하나는 "8로 나누기" 카운터로 구성할 수 있습니다. 2개의 IC는 그림과 같이 "128로 나누기" 주파수 분배기를 형성하기 위해 함께 계단식으로 연결됩니다.
물론 2분할, 5분할 또는 이 둘의 조합으로 구성할 수 있는 TTL 74LS90 프로그래밍 가능 리플 카운터/분할기와 같은 표준 I2C 비동기 카운터도 사용할 수 있습니다. 74LS390은 2, 4, 5, 10, 20, 25, 50, 100 등의 분할 형태로 사용할 수 있는 다양한 "분할" 조합을 갖춘 매우 유연한 듀얼 10진 드라이버 IC입니다.
주파수 분배기
"n으로 나누기" 출력을 생성하기 위해 시퀀스를 자르는 리플 카운터의 이러한 기능은 카운터, 특히 리플 카운터를 주파수 분배기로 사용하여 높은 클록 주파수를 디지털 환경에서 사용하기 더 유용한 값으로 줄일 수 있음을 의미합니다. 시계 및 타이밍 애플리케이션. 예를 들어 디지털 클록을 작동하려면 정확한 1Hz 타이밍 신호가 필요하다고 가정합니다.
Astable 멀티바이브레이터로 구성된 표준 555 타이머 칩을 사용하여 1Hz 구형파 신호를 매우 쉽게 생성할 수 있지만 제조업체의 데이터 시트에 따르면 555 타이머에는 제조업체에 따라 일반적으로 1~2%의 타이밍 오류가 있으며 낮은 경우에도 마찬가지입니다. 1Hz의 주파수에서 이 2%의 타이밍 오류는 좋지 않습니다.
그러나 데이터 시트에는 555 타이머의 최대 작동 주파수가 약 300kHz이고 이 고주파수에서 2% 오류가 여전히 최대 약 6kHz로 크지만 허용될 수 있다고 나와 있습니다. 따라서 262.144kHz라는 더 높은 타이밍 주파수와 18비트 리플(Modulo-18) 카운터를 선택하면 아래와 같이 정밀한 1Hz 타이밍 신호를 쉽게 만들 수 있습니다.
18비트 비동기 리플 카운터의 1Hz 타이밍 신호

물론 이것은 정확한 타이밍 주파수를 생성하는 방법에 대한 매우 단순한 예이지만, 고주파 수정 발진기와 다중 비트 주파수 분배기를 사용하면 시계에서 이벤트 타이밍에 이르기까지 모든 범위의 응용 분야에 사용할 수 있는 정밀 주파수 생성기를 생성할 수 있습니다. 전자 피아노/신디사이저 또는 음악 유형 애플리케이션까지 포함합니다.
불행하게도 비동기 카운터의 주요 단점 중 하나는 게이트의 내부 회로로 인해 입력에 클럭 펄스가 도달하는 것과 출력에 존재하는 것 사이에 약간의 지연이 있다는 것입니다.
비동기 회로에서 이 지연은 비동기 리플 카운터에 "전파 카운터"라는 별명을 부여하는 전파 지연 이라고 하며 일부 고주파수 경우 이 지연은 잘못된 출력 카운트를 생성할 수 있습니다.
큰 비트 리플 카운터 회로에서 개별 단계의 지연을 모두 추가하여 카운터 체인의 끝에서 합산된 지연을 제공하는 경우 입력 신호와 카운트된 출력 신호 간의 시간 차이가 매우 클 수 있습니다. 이것이 비동기 카운터가 일반적으로 많은 수의 비트가 포함된 고주파 카운팅 회로에 사용되지 않는 이유입니다.
또한 카운터의 출력은 서로 고정된 시간 관계를 갖지 않으며 클럭킹 순서로 인해 동일한 순간에 발생하지 않습니다. 즉, 출력 주파수는 일종의 도미노 효과처럼 하나씩 사용 가능해집니다. 그런 다음 비동기 카운터 체인에 더 많은 플립플롭을 추가할수록 정확한 계산을 보장하기 위해 최대 작동 주파수가 낮아집니다. 전파 지연 문제를 극복하기 위해 동기 카운터가 개발되었습니다.
그런 다음 비동기 카운터의 장점 중 일부를 요약하면 다음과 같습니다.
- 비동기 카운터는 토글 또는 D형 플립플롭으로 쉽게 만들 수 있습니다.
- 플립플롭의 클록 입력이 모두 동일한 클록 신호에 의해 구동되지 않기 때문에 이를 "비동기 카운터"라고 합니다.
- 체인의 각 출력은 이전 플립플롭 출력의 상태 변화에 따라 달라집니다.
- 비동기 카운터는 데이터가 한 플립플롭의 출력에서 다음 플립플롭의 입력으로 "리플"하는 것처럼 보이기 때문에 리플 카운터라고도 합니다.
- 이는 "n으로 나누기" 카운터 회로를 사용하여 구현할 수 있습니다.
- 잘린 카운터는 모든 모듈러스 숫자 카운트를 생성할 수 있습니다.
비동기 카운터의 단점:
- 추가 "재동기화" 출력 플립플롭이 필요할 수 있습니다.
- 2n 이 아닌 잘린 시퀀스를 계산하려면 추가 피드백 논리가 필요합니다.
- 비트 수를 많이 계산하면 연속적인 단계의 전파 지연이 바람직하지 않게 커질 수 있습니다.
- 이 지연으로 인해 "전파 카운터"라는 별명이 붙었습니다.
- 높은 클럭킹 주파수에서 계산 오류가 발생합니다.
- 동기식 카운터는 모든 플립플롭에 동일한 클록 신호를 사용하므로 더 빠르고 안정적입니다.