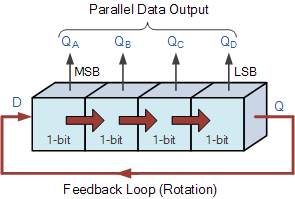
존슨 링 카운터
존슨 링 카운터는 출력이 입력으로 피드백되는 다수의 카운터로 구성됩니다.
이 튜토리얼에서 우리는 Johnson 링 카운터가 시프트 레지스터를 사용하여 생성된 카운터 유형임을 볼 것이며, 이전 시프트 레지스터 튜토리얼에서는 직렬 데이터 신호를 직렬 입력에서 직렬 출력까지 의 입력에 적용하는 경우를 보았습니다. 시프트 레지스터(Shift Register) , 동일한 데이터 시퀀스가 레지스터 체인의 마지막 플립 플립에서 종료됩니다.
레지스터를 통한 데이터의 직렬 이동은 미리 설정된 수의 클록 사이클 후에 발생하므로 SISO 레지스터는 원래 입력 데이터 신호에 대한 일종의 시간 지연 회로 역할을 할 수 있습니다.
하지만 이 시프트 레지스터의 출력을 입력에 다시 연결하여 마지막 플립플롭의 출력 Q D 가 첫 번째 플립플롭 Q A 의 입력이 된다면 어떻게 될까요 ? 그런 다음 시퀀스의 모든 상태에 대해 연속 루프 주위에서 동일한 데이터 비트를 "재순환"하는 폐쇄 루프 회로를 갖게 되며 이것이 링 카운터 의 주요 작동입니다 .
그런 다음 출력을 입력으로 다시 루프함으로써(피드백) 표준 시프트 레지스터 회로를 링 카운터로 변환할 수 있습니다. 아래 회로를 고려하십시오.
4비트 링 카운터
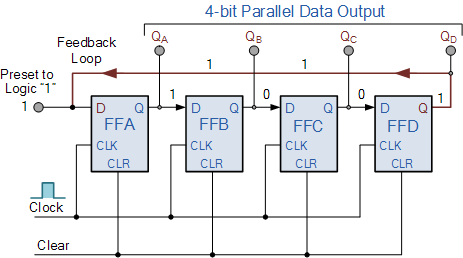
위의 동기식 링 카운터 예는 레지스터의 정확히 하나의 데이터 비트가 논리 "1"로 설정되고 다른 모든 비트는 "0"으로 재설정되도록 사전 설정되어 있습니다. 이를 달성하기 위해 먼저 "CLEAR" 신호가 모든 플립플롭에 함께 적용되어 출력을 논리 "0" 레벨로 "RESET"한 다음 첫 번째 플립플롭의 입력에 "PRESET" 펄스가 적용됩니다. - 클록 펄스가 적용되기 전의 flop ( FFA ). 그러면 단일 논리 "1" 값이 링 카운터의 회로에 배치됩니다.
따라서 각 연속 클록 펄스에서 카운터는 매 4번째 클록 사이클마다 "링" 주위에 4개의 플립플롭 사이에서 동일한 데이터 비트를 반복해서 순환합니다. 그러나 카운터 주위에서 데이터를 올바르게 순환하려면 먼저 적절한 데이터 패턴으로 카운터를 "로드"해야 합니다. 각 클록 사이클에서 출력되는 모든 논리 "0" 또는 모든 논리 "1"은 링 카운터를 무효화하기 때문입니다.
이러한 유형의 데이터 이동을 "회전"이라고 하며 이전 시프트 레지스터와 마찬가지로 링 카운터를 통해 왼쪽에서 오른쪽으로 데이터 비트를 이동한 효과는 타이밍 다이어그램과 함께 다음과 같이 그래픽으로 표시할 수 있습니다.
링 카운터의 회전 운동
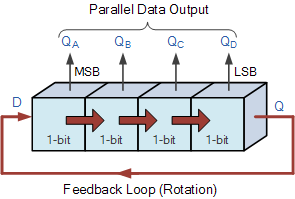
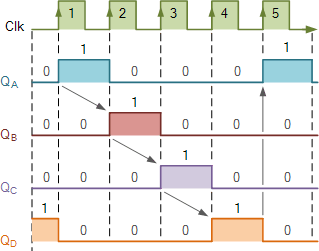
위에 표시된 링 카운터 예제에는 4개의 개별 상태가 있으므로 "모듈로-4" 또는 "mod-4" 카운터라고도 알려져 있으며 각 플립플롭 출력은 1/4 또는 1/4(1 /4) 메인 클록 주파수의 주파수입니다.
카운터의 "MODULO" 또는 "MODULUS"는 카운터가 반복되기 전에 카운트하거나 시퀀스하는 상태의 수이며 링 카운터는 임의의 모듈로 숫자를 출력하도록 만들어질 수 있습니다. "mod-n" 링 카운터에는 "n"개의 서로 다른 출력 상태를 제공하는 단일 데이터 비트를 순환시키기 위해 함께 연결된 "n"개의 플립플롭이 필요합니다.
예를 들어, Mod-8 링 카운터에는 8개의 플립플롭이 필요하고 Mod-16 링 카운터에는 16개의 플립플롭이 필요합니다. 그러나 위의 예에서와 같이 가능한 16개 상태 중 4개만 사용되므로 링 카운터는 출력 상태 사용 측면에서 매우 비효율적입니다.
존슨 링 카운터
존슨 링 카운터 또는 "트위스트 링 카운터"는 위의 표준 링 카운터 와 정확히 동일한 피드백을 갖는 또 다른 시프트 레지스터입니다 . 단, 이번에는 마지막 플립플롭의 반전 출력 Q가 이제 입력 D 에 다시 연결됩니다. 첫 번째 플립플롭은 아래와 같습니다.
이러한 유형의 링 카운터의 가장 큰 장점은 표준 링 카운터에 비해 플립플롭 수가 절반만 필요하고 모듈로 수가 절반으로 줄어든다는 것입니다. 따라서 "n-스테이지" Johnson 카운터는 2n개의 서로 다른 상태 시퀀스를 제공하는 단일 데이터 비트를 순환하므로 "mod-2n 카운터"로 간주될 수 있습니다.
4비트 존슨 링 카운터
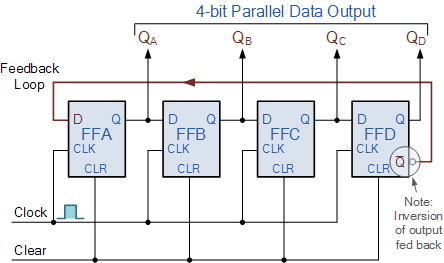
입력 D 로 피드백되기 전에 Q 를 반전시키면 카운터가 다른 방식으로 "계산"됩니다. 4비트 카운터의 경우 일반 링 카운터처럼 고정된 패턴 세트를 통해 계산하는 대신 "0001"(1), "0010"(2), "0100"(4), "1000"(8) 반복하면 Johnson 카운터는 초기 논리 "1"이 이전 논리 "0"을 대체하여 오른쪽으로 통과함에 따라 카운트 업 및 다운됩니다.
4비트 Johnson 링 카운터는 4개의 논리 "0" 블록을 전달한 다음 4개의 논리 "1" 블록을 전달하여 8비트 패턴을 생성합니다. 반전된 출력 Q가 입력 D 에 연결되면 이 8비트 패턴이 계속 반복됩니다. 예를 들어 "1000", "1100", "1110", "1111", "0111", "0011", "0001", "0000"이며 이는 아래 표에 나와 있습니다.
4비트 존슨 링 카운터의 진리표
| 클록 펄스 번호 | FFA | FFB | FFC | FFD |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 |
| 삼 | 1 | 1 | 1 |
0 |
| 4 | 1 | 1 | 1 | 1 |
| 5 | 0 | 1 | 1 | 1 |
| 6 | 0 | 0 | 1 | 1 |
| 7 | 0 | 0 | 0 | 1 |
연속 루프를 중심으로 데이터를 계산하거나 회전하는 것 외에도 링 카운터를 사용하여 데이터 집합 내에서 다양한 패턴이나 숫자 값을 감지하거나 인식할 수도 있습니다. AND 또는 OR 게이트 와 같은 간단한 논리 게이트를 플립플롭의 출력에 연결함으로써 회로는 설정된 숫자 또는 값을 감지하도록 만들 수 있습니다.
표준 2, 3 또는 4단계 Johnson 링 카운터는 피드백 연결을 변경하여 클록 신호의 주파수를 나누는 데 사용할 수도 있으며 3으로 나누기 또는 5로 나누기 출력도 사용할 수 있습니다.
예를 들어, 3단계 존슨 링 카운터는 A , B 및 NOT-B 의 데이터 출력에 연결하여 3상, 120도 위상 편이 구형파 발생기로 사용할 수 있습니다 .
일반적으로 사용 가능한 CD4017과 같은 표준 5단계 Johnson 카운터는 일반적으로 동기식 10진 카운터/분할 회로로 사용됩니다.
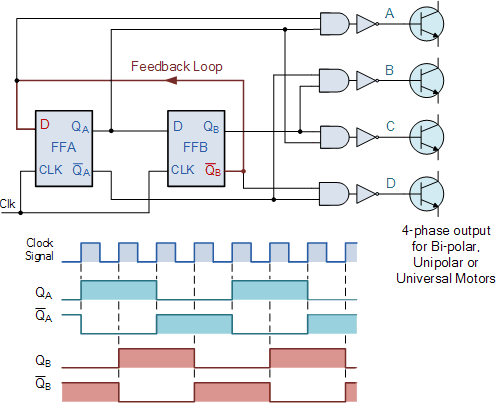
"구적"(사인/코사인) 발진기 또는 생성기라고도 하는 더 작은 2단 회로와 같은 다른 조합을 사용하여 각각 90도 "위상이 다른" 4개의 개별 출력을 생성할 수 있습니다. 다른 하나는 아래와 같이 4단계 타이밍 신호를 생성합니다.
2비트 직교 위상 생성기
| 산출 | ㅏ | 비 | 씨 | 디 |
| QA + QB _ _ | 1 | 0 | 0 | 0 |
| QA + QB _ _ | 0 | 1 | 0 | 0 |
| QA + QB _ _ | 0 | 0 | 1 | 0 |
| QA + QB _ _ | 0 | 0 | 0 | 1 |
| 2비트 직교 발진기, 카운트 시퀀스 | ||||
4개의 출력( A ~ D) 은 서로에 대해 90도 위상 이동되므로 추가 회로와 함께 사용하여 위치 제어를 위한 2상 풀스텝 스테퍼 모터를 구동하거나 모터를 회전시키는 기능을 사용할 수 있습니다. 아래와 같이 특정 위치.
스테퍼 모터 제어
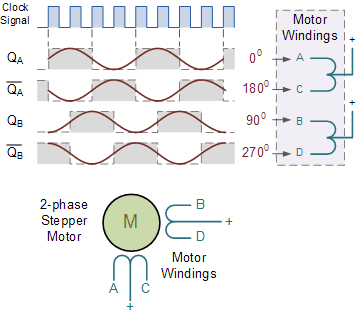
2상(단극) 풀스텝 스테퍼 모터 회로
스테퍼 모터의 회전 속도는 주로 클록 주파수에 따라 달라지며 모터의 "전력" 요구 사항을 구동하려면 추가 회로가 필요합니다. 이 섹션은 독자에게 존슨 링 카운터 와 그 응용 에 대한 기본적인 이해를 제공하기 위한 것이므로 다른 좋은 웹사이트에서는 스테퍼 모터의 유형과 드라이브 요구 사항을 더 자세히 설명합니다.
Johnson 링 카운터는 10개의 활성 HIGH 디코딩 출력이 있는 CD4017 5단계, 10진 존슨 링 카운터 또는 8개의 활성 HIGH 디코딩이 있는 CD4022 4단계, 8분할 Johnson 카운터와 같은 표준 TTL 또는 CMOS IC 형태로 제공됩니다. 출력.