RMS 전압 튜토리얼
정현파의 RMS 또는 유효 값은 등가 DC 공급 장치와 동일한 가열 효과를 제공합니다.
AC 파형 에 대한 튜토리얼에서 우리는 정현파의 RMS 전압 값을 간략하게 살펴보고 이 RMS 값이 등가 DC 전력과 동일한 가열 효과를 제공한다고 말했으며 이 튜토리얼에서는 다음을 살펴보며 이 이론을 좀 더 확장할 것입니다. RMS 전압 및 전류에 대해 자세히 설명합니다.
"RMS"라는 용어는 "Root-Mean-Squared"를 의미합니다. 대부분의 책에서는 이를 "동등한 DC 전력과 동일한 가열 효과를 생성하는 AC 전력의 양" 또는 이와 유사한 것으로 정의하지만 RMS 값은 그 이상입니다.
RMS 값은 순시 값의 제곱 함수의 평균(평균) 값의 제곱근입니다. RMS 값을 정의하는 데 사용되는 기호는 V RMS 또는 I RMS 입니다 .
RMS라는 용어는 시간에 따라 파형의 크기가 변하는 시간에 따라 변하는 정현파 전압, 전류 또는 복잡한 파형을 나타내며 크기가 항상 일정한 DC 회로 분석이나 계산에는 사용되지 않습니다.
등가 DC 회로와 같이 주어진 부하에 동일한 전력을 공급하는 교류 정현파의 등가 RMS 전압 값을 비교하는 데 사용되는 경우 RMS 값을 "유효 값"이라고 하며 일반적으로 다음과 같이 표시됩니다. V eff 또는 I eff .
즉, 유효 값은 동일한 전력을 생성하는 능력 측면에서 시간에 따라 변하는 정현파 파형이 몇 볼트 또는 암페어의 DC와 동일한지를 알려주는 등가 DC 값입니다.
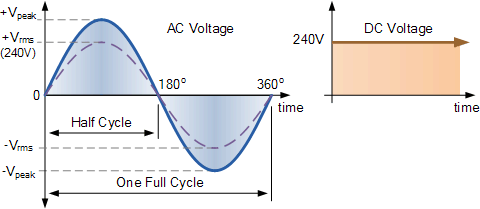
예를 들어, 영국의 국내 주전원 공급 장치는 240Vac입니다. 이 값은 "240 Volts rms"의 유효 값을 나타내는 것으로 가정됩니다. 이는 영국 가정의 벽면 소켓에서 나오는 정현파 RMS 전압이 아래와 같이 240V의 안정적인 DC 전압과 동일한 평균 양의 전력을 생성할 수 있음을 의미합니다.
RMS 전압 등가
그렇다면 정현파의 RMS 전압은 어떻게 계산합니까 ? 정현파 또는 복소 파형의 RMS 전압은 두 가지 기본 방법으로 결정할 수 있습니다.
- 그래픽 방법 – 파형에 여러 개의 중앙 세로좌표를 그려서 비정현파 시변 파형의 RMS 값을 찾는 데 사용할 수 있습니다.
- 분석 방법 – 미적분학을 사용하여 주기적인 전압 또는 전류의 유효 또는 RMS 값을 찾는 수학적 절차입니다.
RMS 전압 그래픽 방법
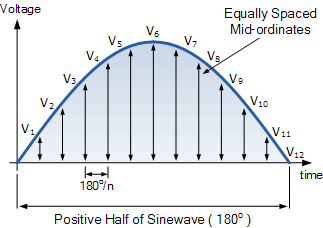
계산 방법은 AC 파형의 양쪽 절반에 대해 동일하지만 이 예에서는 양의 절반 사이클만 고려합니다. 파형을 따라 동일한 간격의 순간 값을 취함으로써 합리적인 정확도로 파형의 유효 또는 rms 값을 찾을 수 있습니다.
파형의 양의 절반은 "n"개의 동일한 부분 또는 중앙 세로좌표 로 분할되며 , 파형을 따라 그려지는 중앙 세로좌표가 많을수록 최종 결과가 더 정확해집니다.
따라서 각 중앙종표의 너비는 0 도가 되고 각 중앙종표의 높이는 파형의 x축을 따라 해당 시점의 파형의 순간값과 동일하게 됩니다.
그래픽 방법
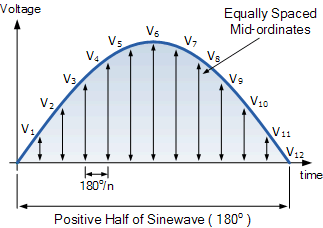
파형(이 경우 전압 파형)의 각 중앙값은 자신을 곱하고(제곱) 다음 값에 더해집니다. 이 방법은 RMS 전압 표현의 "제곱" 또는 제곱 부분을 제공합니다.
다음으로 이 제곱 값을 RMS 전압 표현의 평균 부분 을 제공하는 데 사용되는 중앙 좌표의 수로 나눕니다 . 위의 간단한 예에서는 사용된 중앙 좌표의 수는 12입니다. 마지막으로 이전 결과의 제곱근을 통해 RMS 전압의 루트 부분 을 얻을 수 있습니다 .
그런 다음 rms 전압(V RMS )을 설명하는 데 사용되는 용어를 " 전압 파형의 중앙 세로좌표의 제곱 평균의 제곱근"으로 정의할 수 있으며 이는 다음 과 같이 제공 됩니다 .

위의 간단한 예에서 RMS 전압은 다음과 같이 계산됩니다.
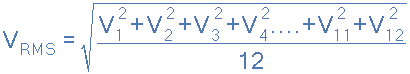
따라서 교류 전압의 피크 전압( V pk )이 20V이고 10개의 중앙 세로값을 취하면 다음과 같이 반주기에 걸쳐 변화하는 것으로 밝혀졌습니다.
| 전압 | 6.2V | 11.8V | 16.2V | 19.0V | 20.0V | 19.0V | 16.2V | 11.8V | 6.2V | 0V |
| 각도 | 18 시 | 36 시 | 54 시 | 72 시 | 90 시 | 108 오 | 126 오 | 144 오 | 162 오 | 180 도 |
따라서 RMS 전압은 다음과 같이 계산됩니다.
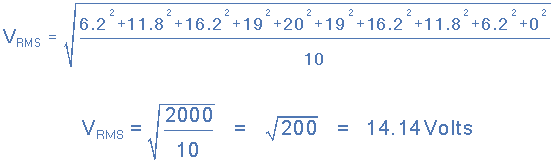
그런 다음 그래픽 방법을 사용하는 RMS 전압 값은 14.14V 로 제공됩니다 .
RMS 전압 분석 방법
위의 그래픽 방법은 본질적으로 대칭 또는 정현파가 아닌 교류 파형의 유효 또는 RMS 전압(또는 전류)을 찾는 매우 좋은 방법입니다. 즉, 파형 모양은 복잡한 파형과 유사합니다.
그러나 순수 정현파 파형을 다룰 때 RMS 값을 찾는 분석적 또는 수학적 방법을 사용하면 생활을 조금 더 쉽게 만들 수 있습니다.
주기적인 정현파 전압은 일정하며 주기가 T 인 V (t) = V max *cos(Ωt) 로 정의할 수 있습니다 . 그런 다음 정현파 전압(V (t) )의 제곱평균제곱근 (rms) 값을 다음과 같이 계산할 수 있습니다 .

0에서 360o 또는 "T"까지의 한계를 통합하면 기간 은 다음과 같습니다.
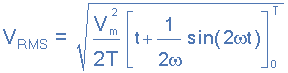
여기서: Vm 은 파형의 피크 또는 최대값입니다. Ω = 2π/T 로 더 나누면 위의 복잡한 방정식도 결국 다음과 같이 줄어듭니다.
RMS 전압 방정식
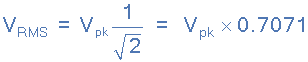
그런 다음 정현파의 RMS 전압( VRMS )은 피크 전압 값에 0.7071을 곱하여 결정됩니다. 이는 1 을 2의 제곱근( 1/√2 ) 으로 나눈 것과 같습니다 .
유효 값이라고도 할 수 있는 RMS 전압은 파형의 크기에 따라 달라지며 파형 주파수나 위상 각도의 함수가 아닙니다.
위의 그래픽 예에서 파형의 피크 전압( V pk )은 20V로 지정되었습니다. 방금 정의한 분석 방법을 사용하여 RMS 전압을 다음과 같이 계산할 수 있습니다.
V RMS = V pk * 0.7071 = 20 x 0.7071 = 14.14V
이 14.14V 값은 이전 그래픽 방법과 동일한 값입니다. 그런 다음 중앙 좌표의 그래픽 방법이나 분석 계산 방법을 사용하여 정현파의 RMS 전압 또는 전류 값을 찾을 수 있습니다.
피크 또는 최대값에 상수 0.7071 을 곱 하면 정현파 에만 적용됩니다. 비정현파 파형의 경우 그래픽 방법을 사용해야 합니다.
그러나 정현파의 피크 또는 최대값을 사용하는 것 외에도 피크 대 피크(V P-P ) 값 또는 평균(V AVG ) 값을 사용하여 다음과 같이 정현파 등가 제곱근 평균 값을 찾을 수도 있습니다.
정현파 RMS 값
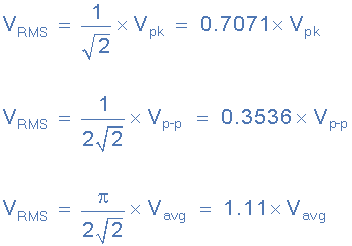
RMS 전압 요약
그런 다음 요약합니다. 교류 전압(또는 전류)을 다룰 때 우리는 전압이나 신호 크기를 어떻게 표현해야 하는지에 대한 문제에 직면하게 됩니다. 한 가지 쉬운 방법은 파형의 피크 값을 사용하는 것입니다. 또 다른 일반적인 방법은 제곱 평균 제곱근 또는 간단히 RMS 값으로 알려진 유효 값을 사용하는 것입니다 .
정현파의 제곱 평균 RMS 값은 모든 순간 값의 평균과 동일하지 않습니다. 전압의 최대값에 대한 전압의 RMS 값의 비율은 전류의 최대값에 대한 전류의 RMS 값의 비율과 같습니다.
전압계나 전류계 등 대부분의 멀티미터는 순수 사인파 파형을 가정하여 RMS 값을 측정합니다. 비정현파 파형의 RMS 값을 찾으려면 "True RMS 멀티미터"가 필요합니다.
정현파의 RMS 값은 동일한 값의 DC 전류와 동일한 발열 효과를 제공합니다. 즉, 직류 전류가 R 옴 의 저항을 통과하면 저항 에서 열로 소비되는 DC 전력은 I 2 R 와트가 됩니다.
그런 다음 교류 전류 i = I max *sinθ가 동일한 저항을 통해 흐른다면 열로 변환된 AC 전력은 I 2 rms *R 와트 가 됩니다 .
그런 다음 교류 전압과 전류를 다룰 때 달리 명시하지 않는 한 RMS 값으로 처리해야 합니다. 따라서 10암페어의 교류는 10암페어의 직류 및 14.14암페어의 최대값과 동일한 가열 효과를 갖습니다.
이제 교류 전압(또는 전류) 파형의 RMS 값을 결정했으므로 다음 자습서에서는 교류 전압의 평균 값 V AVG를 계산하고 마지막으로 두 값을 비교하는 방법을 살펴보겠습니다 .
'전자일기' 카테고리의 다른 글
| harmonics/고조파/배음 아라보자 (1) | 2024.01.03 |
|---|---|
| 반응성 (3) | 2024.01.02 |
| 병렬 공진 회로 (0) | 2024.01.02 |
| 직렬 공진 회로 (1) | 2024.01.02 |
| 병렬 RLC 회로 분석 (0) | 2024.01.02 |