상호 인덕턴스
상호 인덕턴스는 인접한 코일에 전압을 유도할 때 한 코일 자기장이 다른 코일에 미치는 상호 작용입니다.
상호 인덕턴스는 자기적으로 결합된 두 개의 코일 사이의 회로 매개변수이며, 하나의 코일이 인접한 두 번째 코일로 유도되어 생성되는 시변 자속의 비율을 정의합니다.
이전에 우리는 인덕터가 자체 코일 회전 주위의 자기장 변화의 결과로 자체 유도 EMF를 생성하는 것을 보았습니다. 전류가 변화하는 동일한 회로에서 이 EMF가 유도될 때 이 효과를 자기 유도 (L)라고 합니다.
그러나 EMF가 동일한 자기장 내에 위치한 인접한 코일에 유도되면 EMF는 자기적으로, 유도적으로 또는 상호 유도 (M) 에 의해 유도된다고 합니다 . 그런 다음 두 개 이상의 코일이 공통 자속에 의해 자기적으로 연결되면 상호 인덕턴스 특성을 갖는다고 합니다 .
상호 인덕턴스 는 변압기, 모터, 발전기 및 다른 자기장과 상호 작용하는 기타 전기 부품의 기본 작동 원리입니다. 그런 다음 상호 유도를 하나의 코일에 흐르는 전류가 인접한 코일에 전압을 유도하는 것으로 정의할 수 있습니다.
그러나 상호 인덕턴스는 코일의 "부유" 또는 "누설" 인덕턴스가 전자기 유도를 통해 인접한 다른 구성 요소의 작동을 방해할 수 있으므로 나쁜 것일 수도 있으므로 접지 전위에 대한 전기 차폐가 필요할 수 있습니다.
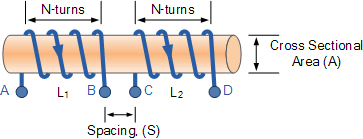
한 코일을 다른 코일에 연결하는 상호 인덕턴스의 양은 두 코일의 상대적 위치에 따라 크게 달라집니다. 한 코일이 다른 코일 옆에 배치되어 물리적 거리가 작으면 첫 번째 코일에서 생성된 거의 모든 자속이 두 번째 코일의 코일 회전과 상호 작용하여 상대적으로 큰 EMF를 유도하여 다음을 생성합니다. 큰 상호 인덕턴스 값.
마찬가지로 두 코일이 서로 더 멀리 떨어져 있거나 각도가 다른 경우 첫 번째 코일에서 두 번째 코일로 유도된 자속의 양은 더 약해져서 유도 EMF가 훨씬 작아지고 따라서 상호 인덕턴스 값도 훨씬 작아집니다. 따라서 상호 인덕턴스의 효과는 두 코일의 상대적 위치 또는 간격(S)에 따라 크게 달라지며 이는 아래에 설명되어 있습니다.
코일 간 상호 인덕턴스
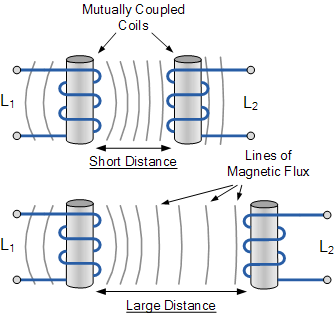
두 코일 사이에 존재하는 상호 인덕턴스는 두 코일을 일반적인 연철 코어에 위치시키거나 변압기에서 볼 수 있는 것처럼 두 코일의 권선 수를 늘리면 크게 증가할 수 있습니다.
두 개의 코일이 일반적인 연철 코어 위에 다른 코일 위에 단단히 감겨 있으면 플럭스 누출로 인한 손실이 매우 작기 때문에 둘 사이에 존재한다고 합니다. 그런 다음 두 코일 사이에 완벽한 자속 결합이 있다고 가정하면 그들 사이에 존재하는 상호 인덕턴스는 다음과 같이 주어질 수 있습니다.
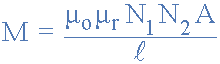
- 어디:
- µ o 는 자유 공간의 투자율입니다(4.π.10 -7 ).
- µ r 은 연철 코어의 상대 투자율입니다.
- N 은 코일 회전 수입니다.
- A 는 단면적(m 2) 입니다.
- ℓ 는 미터 단위의 코일 길이입니다.
상호 유도
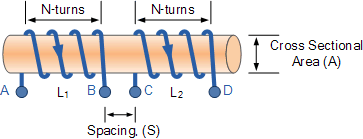
여기서 코일 1에 흐르는 전류 L 1 은 코일 2를 통과하는 일부 자기장 선과 함께 자체 주변에 자기장을 설정하고 L 2는 상호 인덕턴스를 제공합니다. 코일 1의 전류는 I 1 및 N 1 턴이고, 코일 2의 전류는 N 2 턴입니다. 따라서 코일 1에 대해 존재하는 코일 2의 상호 인덕턴스 M 12 는 서로에 대한 위치에 따라 달라지며 다음과 같이 제공됩니다.
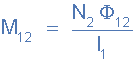
마찬가지로, 코일 1 주위에 전류가 흐를 때 자속 연결 코일 1, L 1 , L 2 는 위의 코일 1 주위에 동일한 전류가 흐를 때 자속 연결 코일 2와 정확히 동일합니다. 코일 2는 M 21 로 정의됩니다 . 이 상호 인덕턴스는 두 코일의 크기, 회전 수, 상대 위치 또는 방향에 관계없이 적용됩니다. 이 때문에 두 코일 사이의 상호 인덕턴스를 M 12 = M 21 = M 으로 쓸 수 있습니다 .
그런 다음 자체 인덕턴스는 인덕터를 단일 회로 요소로 특성화하는 반면 상호 인덕턴스는 거리와 배열에 따라 두 인덕터 또는 코일 사이의 일종의 자기 결합 형태를 의미한다는 것을 알 수 있습니다. 각 개별 코일의 인덕턴스는 다음과 같이 주어진다.

그리고
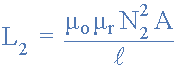
위의 두 방정식을 곱함으로써 두 코일 사이에 존재하는 상호 인덕턴스 M을 각 코일의 자체 인덕턴스로 표현할 수 있습니다.
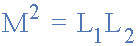
두 코일 사이의 상호 인덕턴스에 대한 최종적이고 보다 일반적인 표현을 제공합니다.
코일 사이의 상호 인덕턴스
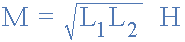
그러나 위의 방정식에서는 자속 누출이 0이고 두 코일 L 1 과 L 2 사이의 자기 결합이 100%라고 가정합니다 . 실제로는 누출과 위치로 인해 항상 약간의 손실이 있으므로 두 코일 사이의 자기 결합은 결코 100%에 도달하거나 초과할 수 없지만 일부 특수 유도 코일에서는 이 값에 매우 가까워질 수 있습니다.
총 자속 중 일부가 두 코일과 연결되면 이 자속 쇄교량은 코일 사이의 가능한 총 자속 쇄교의 일부로 정의될 수 있습니다. 이 분수 값을 결합 계수 라고 하며 문자 k 로 표시됩니다 .
커플링 계수
일반적으로 두 코일 사이에 존재하는 유도 결합의 양은 백분율( % ) 값 대신 0 과 1 사이의 분수로 표시됩니다 . 여기서 0은 유도 결합이 없거나 전혀 없음을 나타내고, 1은 유도 결합이 완전하거나 최대임을 나타냅니다.
즉, k = 1 이면 두 코일이 완벽하게 결합되어 있고, k > 0.5 이면 두 코일이 단단히 결합되어 있다고 하며, k < 0.5 이면 두 코일이 느슨하게 결합되어 있다고 합니다. 그런 다음 완벽한 결합을 가정하는 위의 방정식은 이 결합 계수 k를 고려하여 수정될 수 있으며 다음과 같이 제공됩니다.
코일 사이의 결합 인자
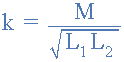
또는
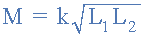
결합 계수 k 가 1 (1) 과 같을 때 한 코일의 모든 자속선이 두 번째 코일의 모든 권선을 절단합니다. 즉, 두 코일이 서로 단단히 결합되어 결과적인 상호 인덕턴스는 다음과 같습니다. 코일의 두 개별 인덕턴스의 기하 평균과 동일해야 합니다.
또한 두 코일의 인덕턴스가 동일하고 같을 때 L 1 은 L 2 와 같습니다 . 두 코일 사이에 존재하는 상호 인덕턴스는 두 개의 동일한 값의 제곱근이 동일하므로 단일 코일의 값과 같습니다. 표시된 대로 하나의 단일 값으로 표시됩니다.
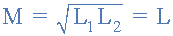
상호 인덕턴스 예 No1
자체 인덕턴스가 각각 75mH와 55mH로 제공되는 두 개의 인덕터는 공통 자기 코어에 나란히 배치되어 첫 번째 코일의 자속선 중 75%가 두 번째 코일을 절단합니다. 두 코일 사이에 존재하는 총 상호 인덕턴스를 계산합니다.
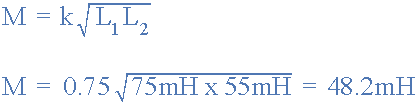
상호 인덕턴스 예 No2
각각 5H와 4H의 인덕턴스를 갖는 두 개의 코일을 비자성 코어에 균일하게 감았을 때 상호 인덕턴스는 1.5H인 것으로 나타났다. 사이에 존재하는 결합 계수를 계산합니다.
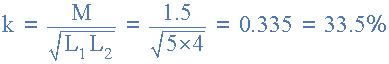
인덕터에 대한 다음 튜토리얼에서는 인덕터를 직렬로 연결하는 방법과 이 조합이 회로의 상호 인덕턴스, 총 인덕턴스 및 유도 전압에 미치는 영향을 살펴봅니다.