위상차 및 위상 변이
위상차는 두 개 이상의 교번 양이 최대값 또는 0 값에 도달할 때 각도 또는 라디안의 차이를 설명하는 데 사용됩니다.
페이저는 회로 주파수가 동일할 때 AC 회로 내 요소의 동작을 분석하는 효과적인 방법입니다. 두 페이저를 합산한 결과는 일부 위상차로 인해 "동위상"인지 "비위상"인지에 따라 상대 위상에 따라 달라집니다.
정현파는 수평축을 따라 시간 영역에서 그래픽으로 표시할 수 있는 교번량입니다. 시간에 따라 변하는 양인 정현파 파형은 시간 π/2 에서 양의 최대값, 시간 3π/2 에서 음의 최대값을 가지며, 0 , π 및 2π 지점 에서 기준선을 따라 0 값이 발생합니다 .
그러나 모든 정현파 가 동시에 0축 지점을 정확하게 통과하는 것은 아니지만 다른 정현파와 비교할 때 일부 값만큼 0o 의 오른쪽이나 왼쪽으로 "이동"할 수 있습니다.
예를 들어, 전압 파형을 전류 파형과 비교합니다. 그러면 두 정현파 파형 사이에 각도 이동 또는 위상차가 생성됩니다. t = 0 에서 0을 통과하지 않는 사인파에는 위상 변화가 있습니다.
정현파라고도 불리는 차이 또는 위상 변화는 파형이 수평 영점 축을 따라 특정 기준점에서 이동한 각도 Φ (그리스 문자 Phi)(도 또는 라디안)입니다. 즉, 위상 변이는 공통 축을 따라 두 개 이상의 파형 사이의 측면 차이이며 동일한 주파수의 정현파 파형은 위상차를 가질 수 있습니다.
교번 파형 의 위상 차이 Φ는 0 에서 최대 기간, 하나의 완전한 사이클 동안 파형의 T 사이에서 달라질 수 있으며 이는 수평 축을 따라 Φ = 0 ~ 2π (라디안) 또는 Φ 사이에 있을 수 있습니다. = 사용된 각도 단위에 따라 0 ~ 360o .
위상차는 시간의 일부를 나타내는 τ (초) 의 시간 이동 (예: +10mS 또는 -50uS ) 으로 표현될 수도 있지만 일반적으로 위상차를 각도 측정으로 표현하는 것이 더 일반적입니다.
그런 다음 이전 정현파 파형에서 개발한 정현파 전압 또는 전류 파형의 순간값에 대한 방정식을 수정하여 파형의 위상각을 고려해야 하며 이 새로운 일반 표현식은 다음과 같습니다.
위상차 방정식
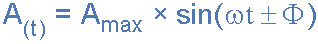
- 어디:
- m – 파형의 진폭입니다.
- Ωt – 파형의 각주파수(라디안/초)입니다.
- Φ (phi) – 파형이 기준점에서 왼쪽이나 오른쪽으로 이동한 위상 각도(도 또는 라디안)입니다.
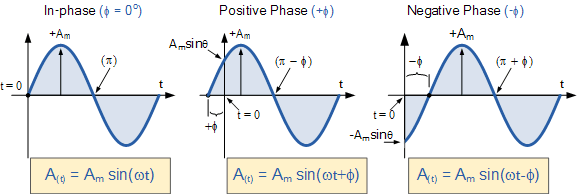
정현파 파형의 양의 기울기가 t = 0 "이전"의 수평 축을 통과하면 파형이 왼쪽으로 이동하여 Φ >0 이 되고 위상 각도는 본질적으로 양의 값이 되며 +Φ는 선두 위상 각도를 제공합니다. 즉, 벡터의 시계 반대 방향 회전을 생성하는 0o 보다 시간적으로 더 일찍 나타납니다.
마찬가지로, 정현파 파형의 양의 기울기가 t = 0 "이후" 어느 시점에 수평 x축을 통과하면 파형은 오른쪽으로 이동하여 Φ <0 이 되고 위상 각도는 본질적 으로 음수인 -Φ 가 됩니다. 0보다 늦게 나타나는 지연 위상 각도는 벡터의 시계 방향 회전을 생성합니다 . 두 경우 모두 아래에 나와 있습니다.
정현파의 위상 관계
먼저, 전압, v 및 전류와 같은 두 개의 교번량 i가 동일한 주파수( Hz) 를 갖는다고 가정해 보겠습니다 . 두 양의 진동수는 각속도와 동일하므로 Ω 도 동일해야 합니다. 따라서 어느 순간에나 전압의 위상 v는 전류의 위상 i 와 동일할 것이라고 말할 수 있습니다 .
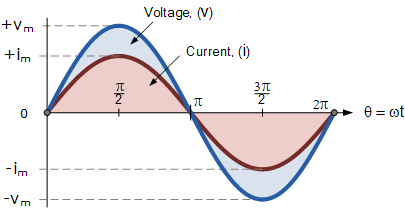
그러면 특정 기간 내의 회전 각도는 항상 동일하며 v 와 i 의 두 양 사이의 위상차는 0이 되고 Φ = 0이 됩니다 . 전압의 주파수 v 와 전류 i 가 동일하기 때문에 둘 다 동시에 하나의 완전한 사이클 동안 최대 양수, 음수 및 0 값에 도달해야 합니다(진폭은 다를 수 있음). 그러면 두 개의 교대 수량 v 와 i가 "동위상"이라고 합니다.
두 개의 사인파형 - "동위상"
이제 전압 v 와 전류 i 사이에 30o 의 위상차가 있으므로 ( Φ = 30o 또는 π / 6 라디안) 이라고 가정 해 보겠습니다. 두 개의 교번하는 양이 동일한 속도로 회전하므로, 즉 동일한 주파수를 가지므로 이 위상차는 모든 순간에 일정하게 유지됩니다. 그러면 두 양 사이 의 30 ° 의 위상차는 아래와 같이 phi, Φ 로 표시됩니다.
정현파의 위상차
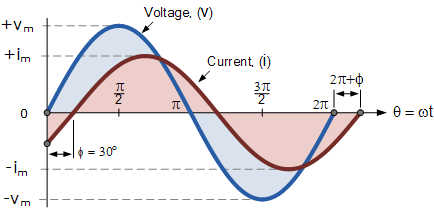
위의 전압 파형은 수평 기준 축을 따라 0에서 시작하지만 동일한 순간에 전류 파형의 값은 여전히 음수이며 30 시가 될 때까지 이 기준 축을 교차하지 않습니다. 그런 다음 전류가 수평 기준 축을 통과하여 최대 피크에 도달하고 전압 파형 이후 0 값에 도달함에 따라 두 파형 사이에 위상 차이가 존재합니다.
두 파형은 더 이상 "동위상"이 아니므로 phi, Φ 에 의해 결정된 양만큼 "위상이 달라"야 하며 이 예에서는 이는 30o 입니다 . 따라서 우리는 두 파형이 이제 30o 위상차가 있다고 말할 수 있습니다. 전류 파형은 위상각 Φ 만큼 전압 파형보다 "지연"되어 있다고 할 수도 있습니다 . 그런 다음 위의 예에서 두 파형에는 지연 위상차가 있으므로 위의 전압과 전류에 대한 표현식은 다음과 같이 제공됩니다.
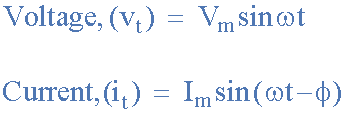
전류, i는 전압, v는 위상각 Φ 에 따라 "지연"됩니다.
마찬가지로, 전류 i 가 양수 값을 갖고 기준 축을 교차하여 전압 v 이전 어느 시점에 최대 피크 및 0 값에 도달하면 전류 파형은 일부 위상 각도만큼 전압을 "리딩"합니다. 그런 다음 두 파형에 선행 위상차가 있다고 하며 전압과 전류 모두에 대한 표현은 다음과 같습니다.
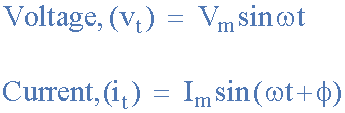
여기서 전류, i는 위상각 Φ 만큼 전압 v를 "리드"합니다.
사인파의 위상 각도는 동일한 참조 축에 표시된 동일한 주파수의 두 정현파 파형 사이의 관계를 나타내기 위해 "진행" 및 "지연"이라는 용어를 사용하여 하나의 사인파와 다른 사인파의 관계를 설명하는 데 사용할 수 있습니다. . 위의 예에서 두 파형은 30 ° 만큼 위상이 다릅니다 . 따라서 우리는 우리가 기준으로 선택한 것에 따라 i 가 v 보다 뒤떨어진다고 정확하게 말할 수도 있고, v가 i 보다 30o 앞선다고 말할 수도 있습니다.
두 파형 사이의 관계와 결과 위상 각도는 각 파형이 양수 또는 음수 "동일한 기울기" 방향으로 통과하는 수평 영점 축을 따라 어디에서나 측정할 수 있습니다.
AC 전원 회로에서 동일한 회로 내의 전압과 전류 사인파 간의 관계를 설명하는 이러한 기능은 매우 중요하며 AC 회로 분석의 기초를 형성합니다.
코사인 파형
따라서 이제 우리는 다른 사인파와 비교할 때 파형이 0o 의 오른쪽이나 왼쪽으로 "이동"하면 이 파형의 표현 은 Am sin(Ωt ± Φ ) 가 된다는 것을 알고 있습니다 . 그러나 파형이 기준 파형 앞에서 90o 또는 π /2 라디안 으로 양의 기울기로 수평 0축을 교차하는 경우 해당 파형을 코사인 파형 이라고 하며 표현은 다음과 같습니다 .
코사인 표현
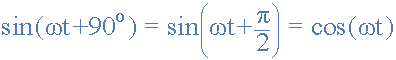
간단히 "cos"라고 불리는 코사인 파는 전기 공학에서 사인파만큼 중요합니다. 코사인파는 사인파와 동일한 모양을 가지고 있습니다. 즉, 정현파 함수이지만 + 90o 또는 1/4 기간만큼 이동합니다.
사인파와 코사인파의 차이점
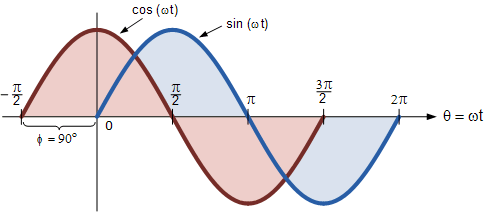
또는 사인파는 다른 방향으로 -90 ° 만큼 이동된 코사인파라고 말할 수도 있습니다 . 어느 쪽이든 각도가 있는 사인파나 코사인파를 처리할 때 다음 규칙이 항상 적용됩니다.
사인파와 코사인파 관계
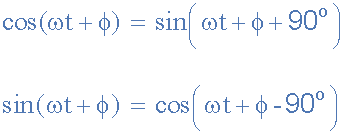
두 정현파 파형을 비교할 때 양의 진폭을 갖는 사인 또는 코사인으로 관계를 표현하는 것이 더 일반적이며 이는 다음 수학적 항등식을 사용하여 달성됩니다.
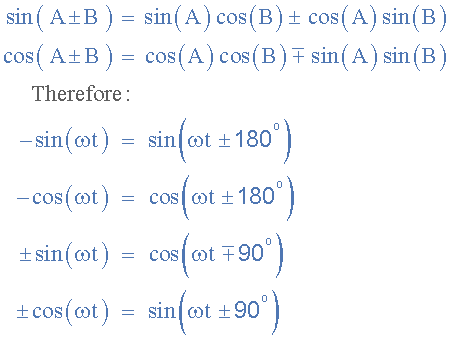
위의 관계를 사용하여 사인파에서 각도 또는 위상 차이가 있거나 없는 모든 정현파를 코사인파로 또는 그 반대로 변환할 수 있습니다.
페이저 에 대한 다음 튜토리얼에서는 두 개 이상의 페이저의 수학적 추가와 관련된 일부 페이저 대수와 함께 단일 위상 AC 수량의 페이저 표현을 살펴봄으로써 두 정현파 간의 위상 차이를 표현하거나 비교하는 그래픽 방법을 사용할 것입니다
'전자일기' 카테고리의 다른 글
| 복소수 및 페이저에대해 아라보자자자아!!!싹다김치 (2) | 2023.12.24 |
|---|---|
| AC회로에사용되는페이져다이어그램및페이저대수학!아라라라보자 (1) | 2023.12.23 |
| 사인파형? 사인누쇠달웨이브뽐? Sinusoidal Waveforms! 아라보자 (1) | 2023.12.22 |
| AC 파형 및 AC 회로 이론 뽀개기 (1) | 2023.12.22 |
| 위상 분배기에 대해 아라보자 페이지시프터히히 (1) | 2023.12.22 |