전자일기

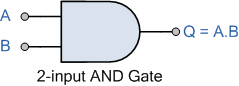
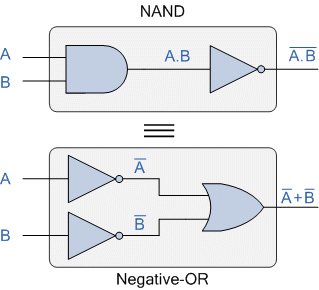
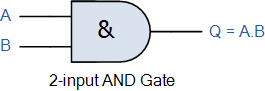
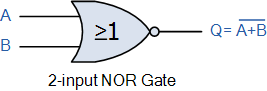
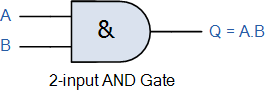
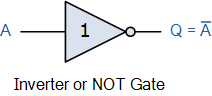
제품 합계 Sum of Product 표현식은 두 개 이상의 제품을 합산하여 출력을 생성하는 논리 AND 함수와 동일합니다. 부울 대수는 표준 논리 게이트의 전환 동작을 나타내는 간단하고 효과적인 방법이며 특정 논리 연산을 수행하는 데 필요한 논리 게이트 수를 줄이는 데 도움이 되는 일련의 규칙 또는 법칙이 발명되었습니다. 곱의 합(Sum-of-Product) 형식은 입력의 서로 다른 "곱" 용어를 함께 "합산"하는 부울 대수 표현입니다. 부울 대수학은 스위칭 이론에서 "풀 세트"라고도 알려진 AND , OR 및 NOT 게이트 기능 과 같은 게이트 및 스위칭 회로를 분석하는 데 사용하는 디지털 논리 수학입니다 . 표준 수학에서는 두 개 이상의 숫자를 곱하여 얻은 숫자 또는 수량을 곱이라고 합니다 . 예를..

스위칭 이론 스위칭 이론은 스위치를 사용하여 디지털 회로의 논리 설계를 위한 부울 표현식과 논리 게이트를 구현하는 것에 관한 것입니다. 스위칭 이론을 통해 우리는 디지털 논리 게이트 와 관련하여 부울 대수와 2단계 논리 함수 간의 작동 및 관계를 이해할 수 있습니다 . 스위칭 이론은 출력 상태 또는 조건을 생성하는 입력 요소의 상호 연결로 볼 때 디지털 회로의 이론적 지식과 개념을 더욱 발전시키는 데 사용될 수 있습니다. 입력과 출력이 0 과 1 의 서로 다른 두 논리 값 사이에서 전환될 수 있는 디지털 논리 게이트는 부울 대수를 사용하여 수학적으로 간단하게 정의할 수 있습니다. 그러나 TRUE 또는 FALSE뿐만 아니라 HIGH 또는 LOW, "1" 또는 "0", "ON" 또는 "OFF"의 두 가지 디..

드모건의 정리 DeMorgan의 정리와 법칙을 사용하여 NAND 및 NOR 게이트의 등가성을 찾을 수 있습니다. DeMorgan의 정리는 OR을 AND 로 , AND를 OR 로 변경하여 다양한 부울 대수식을 풀기 위해 두 세트의 규칙 또는 법칙을 사용합니다. 부울 대수학은 일련의 법칙과 규칙을 사용하여 디지털 입력 또는 출력 조건을 나타내는 데 사용되는 "0"과 "1"을 사용하여 디지털 논리 회로의 작동을 정의합니다. 부울 대수학은 이러한 0과 1을 사용하여 논리 AND , OR 및 NOT (또는 반전) 연산의 디지털 연산뿐만 아니라 XOR (Exclusive-OR) 과 같은 다른 논리 연산을 표현하는 방법 을 정의하는 진리표와 수학적 표현을 생성 합니다. 기능. George Boole의 일련의 법칙과 ..

부울 대수학 예 부울 대수학 법칙을 사용하여 디지털 게이트 수를 줄이는 방법에 대한 부울 대수학 예 이 부울 대수 예제 튜토리얼에서는 부울 대수 법칙을 사용하여 디지털 로직 설계 내에서 불필요한 로직 게이트를 식별하여 전력 소비와 비용을 모두 절약하는 데 필요한 게이트 수를 줄일 수 있음을 살펴보겠습니다. 우리는 이 섹션 전체에서 디지털 논리 함수가 부울 대수 표현이나 논리 게이트 진리표로 정의되고 표시될 수 있다는 것을 살펴보았습니다. 따라서 여기에 부울 대수를 사용하여 더 큰 디지털 논리 회로를 단순화할 수 있는 방법에 대한 몇 가지 예가 있습니다 . 부울 대수학 예제 No1 다음 회로의 C , D , Q 지점에서 논리 기능에 대한 진리표를 구성 하고 전체 회로를 대체하는 데 사용할 수 있는 단일 논..

부울 대수학 진리표 부울 대수 표현식을 사용하여 해당 기능에 대한 디지털 논리 진리표를 구성할 수 있습니다. 표준 부울 표현식뿐만 아니라 논리 게이트 또는 회로의 입력 및 출력 정보를 표준 부울 대수 진리표로 플롯하여 시스템의 스위칭 기능을 시각적으로 표현할 수 있습니다. 논리 게이트 함수의 부울 표현을 나타내는 데 사용되는 테이블을 일반적으로 진리표 라고 합니다 . 논리 게이트 진리표는 게이트 또는 회로에 대한 가능한 각 입력 조합과 이러한 입력 조합에 따른 결과 출력을 보여줍니다. 예를 들어, 입력 변수가 A 및 B 로 표시된 단일 2입력 논리 회로를 생각해 보세요 . 두 개의 입력에 대해 "4"개의 가능한 입력 조합 또는 "OFF" 및 "ON"의 2 2가 있습니다 . 그러나 부울 표현식, 특히 논리..

부울 대수학의 법칙 부울 대수학은 일련의 법칙과 규칙을 사용하여 디지털 논리 회로의 작동을 정의합니다. 특정 논리 연산을 수행하는 데 필요한 논리 게이트 수를 줄이는 데 도움이 되는 일련의 규칙 또는 부울 대수학 표현식이 발명되어 일반적으로 부울 대수학 법칙 으로 알려진 함수 또는 정리 목록이 생성됩니다 . 디지털 입력 또는 출력을 나타내는 데 사용되는 논리 기호 "0"과 "1"뿐만 아니라 이를 각각 영구적인 "개방" 또는 "폐쇄" 회로 또는 접점에 대한 상수로 사용할 수도 있습니다. 부울 대수학은 디지털 게이트와 회로를 분석하는 데 사용하는 수학입니다. 필요한 논리 게이트 수를 줄이기 위해 이러한 "부울 법칙"을 사용하여 복잡한 부울 표현식을 줄이고 단순화할 수 있습니다. 따라서 부울 대수학은 부울 표..

논리 NOR 기능 논리 NOR 함수 출력은 모든 입력이 거짓인 경우에만 참이고, 그렇지 않으면 출력은 항상 거짓입니다. 논리 NOR 기능은 두 개의 개별 논리 기능인 Not 기능과 OR 기능(NOT-OR)을 함께 연결하여 하나의 단일 논리 기능을 구성하는 조합으로 출력이 반전된다는 점을 제외하면 OR 기능과 동일합니다. NOR 게이트를 생성하기 위해 OR 함수와 NOT 함수는 A + B 와 같은 부울 표현식으로 제공되는 연산과 직렬로 함께 연결됩니다. 논리 NOR 기능은 "모든" 입력이 존재하지 않는 경우에만 생성 및 출력하며 부울 대수 용어로 모든 입력이 FALSE 인 경우에만 출력은 TRUE 가 됩니다 . 스위치 표현 NOR 함수 의 진리표는 NOR 게이트가 OR 게이트 의 역동작을 수행하기 때문에 ..

논리 AND 기능 논리 AND 함수 출력은 모든 입력이 참인 경우에만 참이고, 그렇지 않으면 출력은 거짓입니다. 부울 대수학은 논리 AND 함수와 같은 각 부울 함수가 일반적으로 하나 이상의 입력 값을 가지며 이러한 입력 값을 기반으로 출력 결과를 생성하는 논리 함수를 기반으로 합니다. 입력에는 0 또는 1의 두 가지 값 중 하나가 있습니다. 1854년에 조지 불(George Boole)은 "군" 또는 "집합" 이론의 단순화된 버전을 기반으로 한 "사고의 법칙"에 대한 조사를 수행했으며 이로부터 부울 대수학이 개발되었습니다. 부울 대수학은 논리와 집합 연산이 둘 다 "TRUE" 또는 "FALSE"이지만 동시에 둘 다는 아니라는 이론을 주로 다룹니다. 예를 들어, A + A = A 이고 일반 대수학에서는 ..

로직 NAND 기능 논리 NAND 기능 출력은 모든 입력이 참일 때만 거짓이고, 그렇지 않으면 출력은 항상 참입니다. 논리 NAND 기능은 두 개의 별도 논리 기능인 AND 기능과 NOT 기능(NOT-AND)을 직렬로 조합한 것입니다. 논리 NAND 함수는 AB 의 불리언 표현으로 표현될 수 있습니다. 논리 NAND 기능은 "모든" 입력이 존재할 때 출력을 생성하지 않으며 부울 대수학 용어로 모든 입력이 TRUE인 경우에만 출력이 FALSE가 됩니다. 스위치 표현 NAND 함수의 진리표는 NAND 게이트가 AND 게이트의 역연산을 수행하기 때문에 이전 AND 함수의 진리표와 반대입니다. 즉, NAND 게이트는 기본 AND 게이트의 보완입니다. NAND 기능 진리표 스위치 A 스위치 B 산출 설명 0 0 ..

논리 NOT 기능 논리 NOT 함수 출력은 단일 입력이 거짓일 때 참이고, 단일 입력이 참일 때 거짓입니다. 로직 NOT 기능은 로직 레벨 "1"의 입력을 로직 레벨 "0"의 출력으로 또는 그 반대로 변경하는 단순한 단일 입력 인버터입니다. "논리 NOT 함수"는 출력 상태가 입력 상태와 동일하지 않기 때문에 일반적으로 반전 연산을 나타내는 입력 기호 위에 막대 또는 윗줄( ̅ )로 표시되는 부울 표현식을 사용하므로 이름이 다음과 같습니다. 인버터). NOT 게이트 는 논리 INVERT 또는 COMPLEMENTATION 기능을 수행하므로 신호를 반전시키기 때문에 일반적으로 인버터 로 알려져 있습니다. 논리 회로에서 이 부정은 일반적으로 닫힌 스위치로 표현될 수 있습니다. 논리 NOT 기능의 스위치 표현 ..